Variational Quantum Optimization with Continuous Bandits
Paper and Code
Feb 06, 2025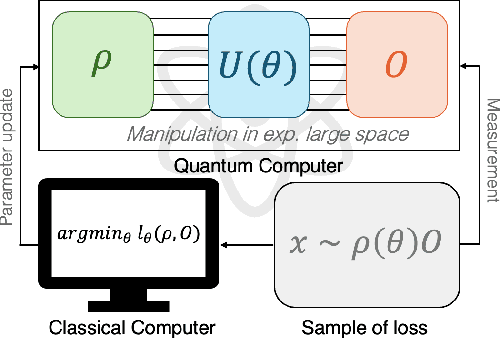
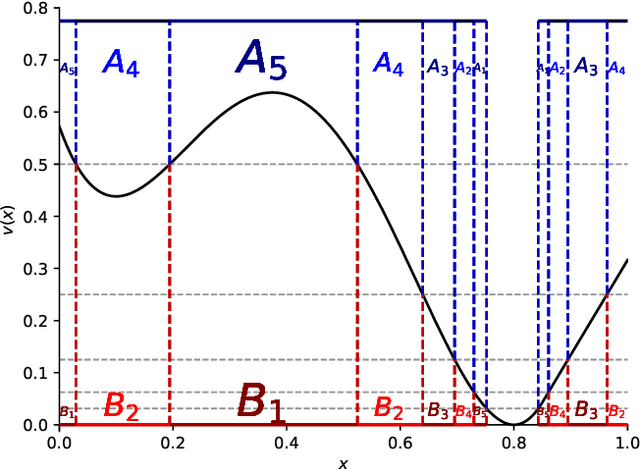
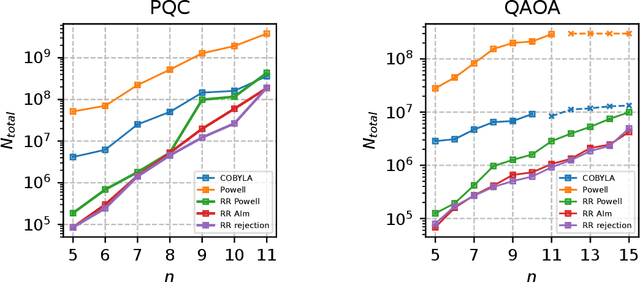
We introduce a novel approach to variational Quantum algorithms (VQA) via continuous bandits. VQA are a class of hybrid Quantum-classical algorithms where the parameters of Quantum circuits are optimized by classical algorithms. Previous work has used zero and first order gradient based methods, however such algorithms suffer from the barren plateau (BP) problem where gradients and loss differences are exponentially small. We introduce an approach using bandits methods which combine global exploration with local exploitation. We show how VQA can be formulated as a best arm identification problem in a continuous space of arms with Lipschitz smoothness. While regret minimization has been addressed in this setting, existing methods for pure exploration only cover discrete spaces. We give the first results for pure exploration in a continuous setting and derive a fixed-confidence, information-theoretic, instance specific lower bound. Under certain assumptions on the expected payoff, we derive a simple algorithm, which is near-optimal with respect to our lower bound. Finally, we apply our continuous bandit algorithm to two VQA schemes: a PQC and a QAOA quantum circuit, showing that we significantly outperform the previously known state of the art methods (which used gradient based methods).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge