Partial Distribution Matching via Partial Wasserstein Adversarial Networks

This paper studies the problem of distribution matching (DM), which is a fundamental machine learning problem seeking to robustly align two probability distributions. Our approach is established on a relaxed formulation, called partial distribution matching (PDM), which seeks to match a fraction of the distributions instead of matching them completely. We theoretically derive the Kantorovich-Rubinstein duality for the partial Wasserstain-1 (PW) discrepancy, and develop a partial Wasserstein adversarial network (PWAN) that efficiently approximates the PW discrepancy based on this dual form. Partial matching can then be achieved by optimizing the network using gradient descent. Two practical tasks, point set registration and partial domain adaptation are investigated, where the goals are to partially match distributions in 3D space and high-dimensional feature space respectively. The experiment results confirm that the proposed PWAN effectively produces highly robust matching results, performing better or on par with the state-of-the-art methods.

SE(3)-bi-equivariant Transformers for Point Cloud Assembly

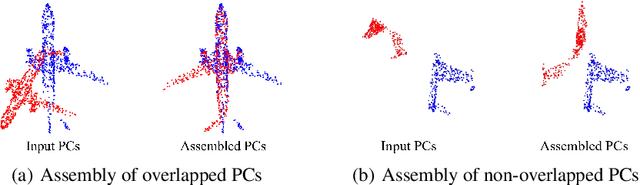
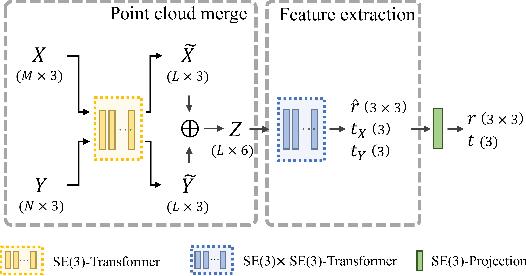
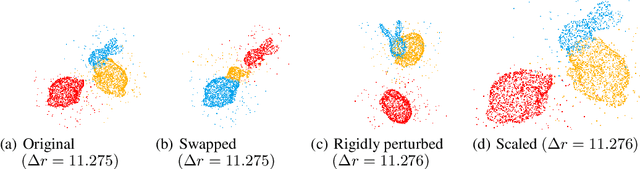
Given a pair of point clouds, the goal of assembly is to recover a rigid transformation that aligns one point cloud to the other. This task is challenging because the point clouds may be non-overlapped, and they may have arbitrary initial positions. To address these difficulties, we propose a method, called SE(3)-bi-equivariant transformer (BITR), based on the SE(3)-bi-equivariance prior of the task: it guarantees that when the inputs are rigidly perturbed, the output will transform accordingly. Due to its equivariance property, BITR can not only handle non-overlapped PCs, but also guarantee robustness against initial positions. Specifically, BITR first extracts features of the inputs using a novel $SE(3) \times SE(3)$-transformer, and then projects the learned feature to group SE(3) as the output. Moreover, we theoretically show that swap and scale equivariances can be incorporated into BITR, thus it further guarantees stable performance under scaling and swapping the inputs. We experimentally show the effectiveness of BITR in practical tasks.

Solving Kernel Ridge Regression with Gradient-Based Optimization Methods

Kernel ridge regression, KRR, is a non-linear generalization of linear ridge regression. Here, we introduce an equivalent formulation of the objective function of KRR, opening up both for using other penalties than the ridge penalty and for studying kernel ridge regression from the perspective of gradient descent. Using a continuous-time perspective, we derive a closed-form solution, kernel gradient flow, KGF, with regularization through early stopping, which allows us to theoretically bound the differences between KGF and KRR. We generalize KRR by replacing the ridge penalty with the $\ell_1$ and $\ell_\infty$ penalties and utilize the fact that analogously to the similarities between KGF and KRR, the solutions obtained when using these penalties are very similar to those obtained from forward stagewise regression (also known as coordinate descent) and sign gradient descent in combination with early stopping. Thus the need for computationally heavy proximal gradient descent algorithms can be alleviated. We show theoretically and empirically how these penalties, and corresponding gradient-based optimization algorithms, produce signal-driven and robust regression solutions, respectively. We also investigate kernel gradient descent where the kernel is allowed to change during training, and theoretically address the effects this has on generalization. Based on our findings, we propose an update scheme for the bandwidth of translational-invariant kernels, where we let the bandwidth decrease to zero during training, thus circumventing the need for hyper-parameter selection. We demonstrate on real and synthetic data how decreasing the bandwidth during training outperforms using a constant bandwidth, selected by cross-validation and marginal likelihood maximization. We also show that using a decreasing bandwidth, we are able to achieve both zero training error and a double descent behavior.

Controlled Descent Training

In this work, a novel and model-based artificial neural network (ANN) training method is developed supported by optimal control theory. The method augments training labels in order to robustly guarantee training loss convergence and improve training convergence rate. Dynamic label augmentation is proposed within the framework of gradient descent training where the convergence of training loss is controlled. First, we capture the training behavior with the help of empirical Neural Tangent Kernels (NTK) and borrow tools from systems and control theory to analyze both the local and global training dynamics (e.g. stability, reachability). Second, we propose to dynamically alter the gradient descent training mechanism via fictitious labels as control inputs and an optimal state feedback policy. In this way, we enforce locally $\mathcal{H}_2$ optimal and convergent training behavior. The novel algorithm, \textit{Controlled Descent Training} (CDT), guarantees local convergence. CDT unleashes new potentials in the analysis, interpretation, and design of ANN architectures. The applicability of the method is demonstrated on standard regression and classification problems.

On the Interpretability of Regularisation for Neural Networks Through Model Gradient Similarity

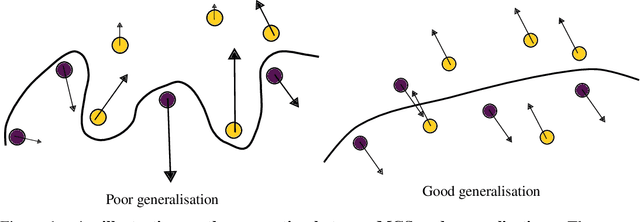
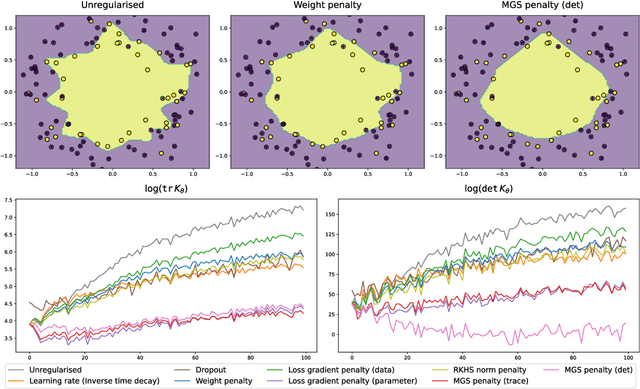
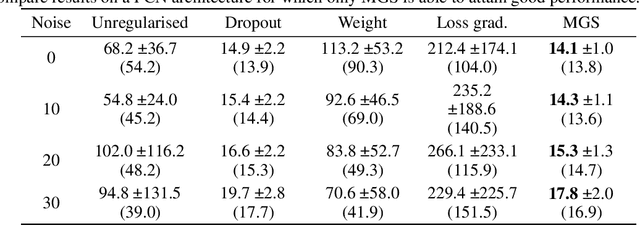
Most complex machine learning and modelling techniques are prone to over-fitting and may subsequently generalise poorly to future data. Artificial neural networks are no different in this regard and, despite having a level of implicit regularisation when trained with gradient descent, often require the aid of explicit regularisers. We introduce a new framework, Model Gradient Similarity (MGS), that (1) serves as a metric of regularisation, which can be used to monitor neural network training, (2) adds insight into how explicit regularisers, while derived from widely different principles, operate via the same mechanism underneath by increasing MGS, and (3) provides the basis for a new regularisation scheme which exhibits excellent performance, especially in challenging settings such as high levels of label noise or limited sample sizes.

Bandwidth Selection for Gaussian Kernel Ridge Regression via Jacobian Control

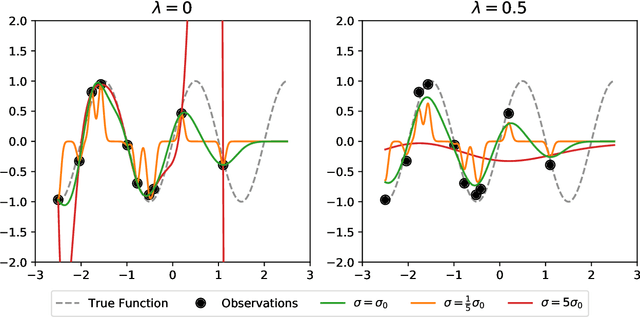
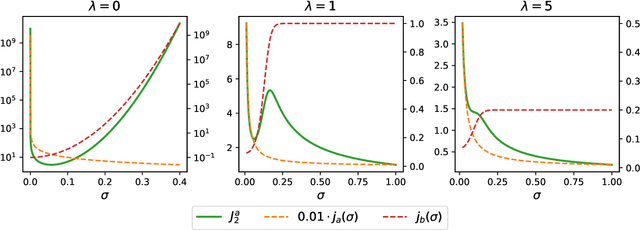
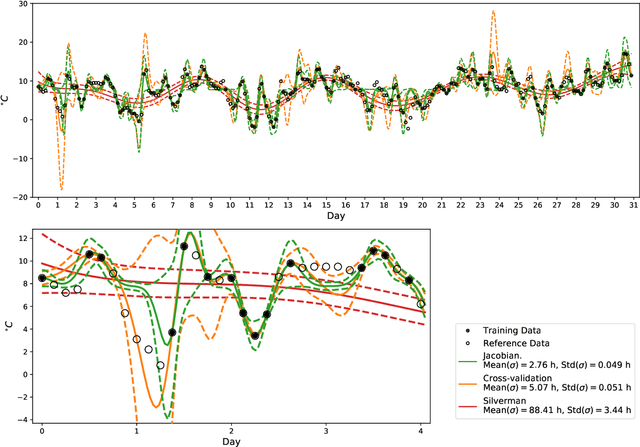
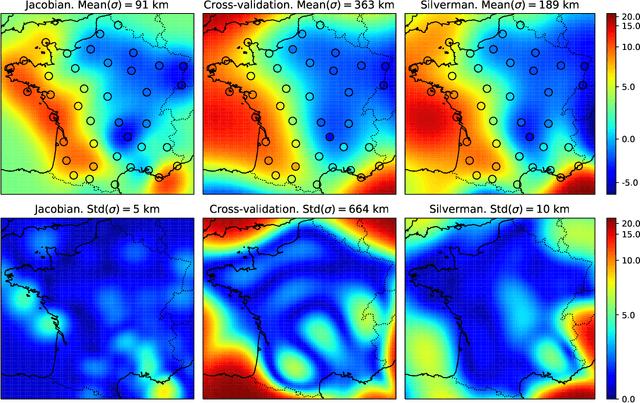
Most machine learning methods depend on the tuning of hyper-parameters. For kernel ridge regression (KRR) with the Gaussian kernel, the hyper-parameter is the bandwidth. The bandwidth specifies the length-scale of the kernel and has to be carefully selected in order to obtain a model with good generalization. The default method for bandwidth selection is cross-validation, which often yields good results, albeit at high computational costs. Furthermore, the estimates provided by cross-validation tend to have very high variance, especially when training data are scarce. Inspired by Jacobian regularization, we formulate how the derivatives of the functions inferred by KRR with the Gaussian kernel depend on the kernel bandwidth. We then use this expression to propose a closed-form, computationally feather-light, bandwidth selection method based on controlling the Jacobian. In addition, the Jacobian expression illuminates how the bandwidth selection is a trade-off between the smoothness of the inferred function, and the conditioning of the training data kernel matrix. We show on real and synthetic data that compared to cross-validation, our method is considerably more stable in terms of bandwidth selection, and, for small data sets, provides better predictions.

Robust Neural Network Classification via Double Regularization

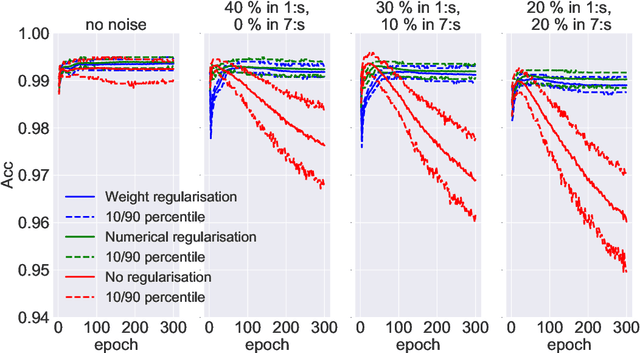
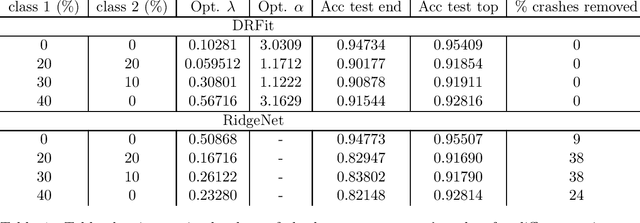
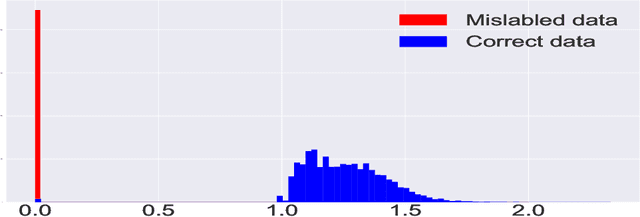
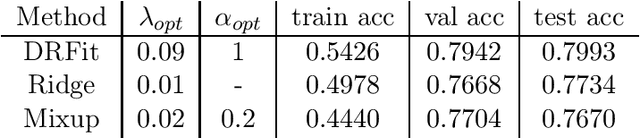
The presence of mislabeled observations in data is a notoriously challenging problem in statistics and machine learning, associated with poor generalization properties for both traditional classifiers and, perhaps even more so, flexible classifiers like neural networks. Here we propose a novel double regularization of the neural network training loss that combines a penalty on the complexity of the classification model and an optimal reweighting of training observations. The combined penalties result in improved generalization properties and strong robustness against overfitting in different settings of mislabeled training data and also against variation in initial parameter values when training. We provide a theoretical justification for our proposed method derived for a simple case of logistic regression. We demonstrate the double regularization model, here denoted by DRFit, for neural net classification of (i) MNIST and (ii) CIFAR-10, in both cases with simulated mislabeling. We also illustrate that DRFit identifies mislabeled data points with very good precision. This provides strong support for DRFit as a practical of-the-shelf classifier, since, without any sacrifice in performance, we get a classifier that simultaneously reduces overfitting against mislabeling and gives an accurate measure of the trustworthiness of the labels.

Non-linear, Sparse Dimensionality Reduction via Path Lasso Penalized Autoencoders

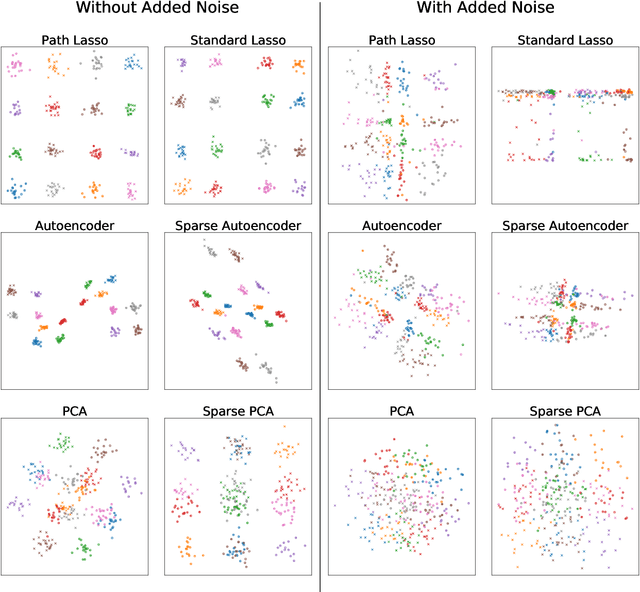
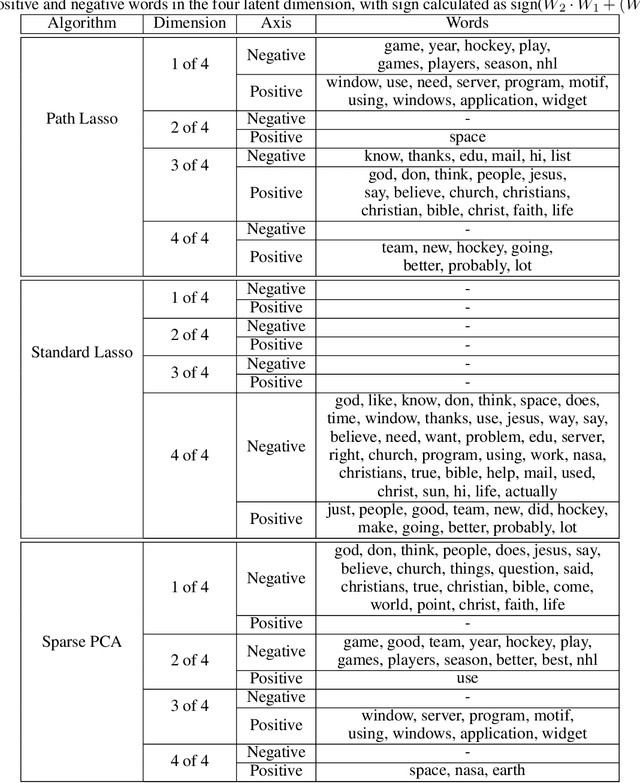
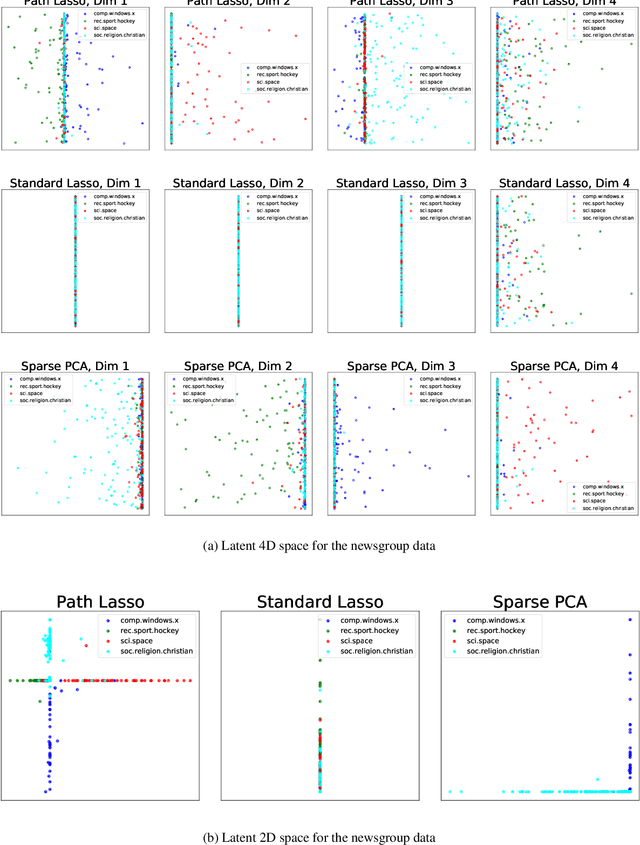
High-dimensional data sets are often analyzed and explored via the construction of a latent low-dimensional space which enables convenient visualization and efficient predictive modeling or clustering. For complex data structures, linear dimensionality reduction techniques like PCA may not be sufficiently flexible to enable low-dimensional representation. Non-linear dimension reduction techniques, like kernel PCA and autoencoders, suffer from loss of interpretability since each latent variable is dependent of all input dimensions. To address this limitation, we here present path lasso penalized autoencoders. This structured regularization enhances interpretability by penalizing each path through the encoder from an input to a latent variable, thus restricting how many input variables are represented in each latent dimension. Our algorithm uses a group lasso penalty and non-negative matrix factorization to construct a sparse, non-linear latent representation. We compare the path lasso regularized autoencoder to PCA, sparse PCA, autoencoders and sparse autoencoders on real and simulated data sets. We show that the algorithm exhibits much lower reconstruction errors than sparse PCA and parameter-wise lasso regularized autoencoders for low-dimensional representations. Moreover, path lasso representations provide a more accurate reconstruction match, i.e. preserved relative distance between objects in the original and reconstructed spaces.

Flexible, Non-parametric Modeling Using Regularized Neural Networks

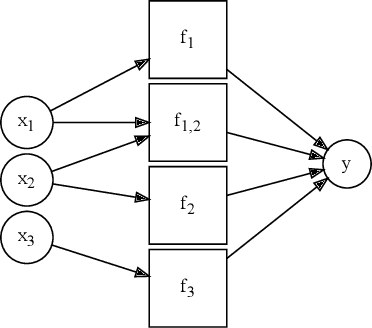
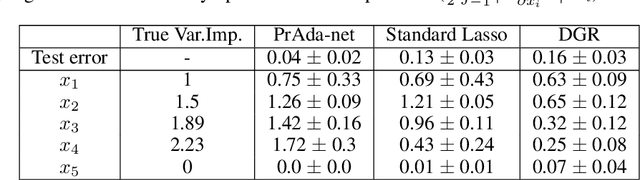
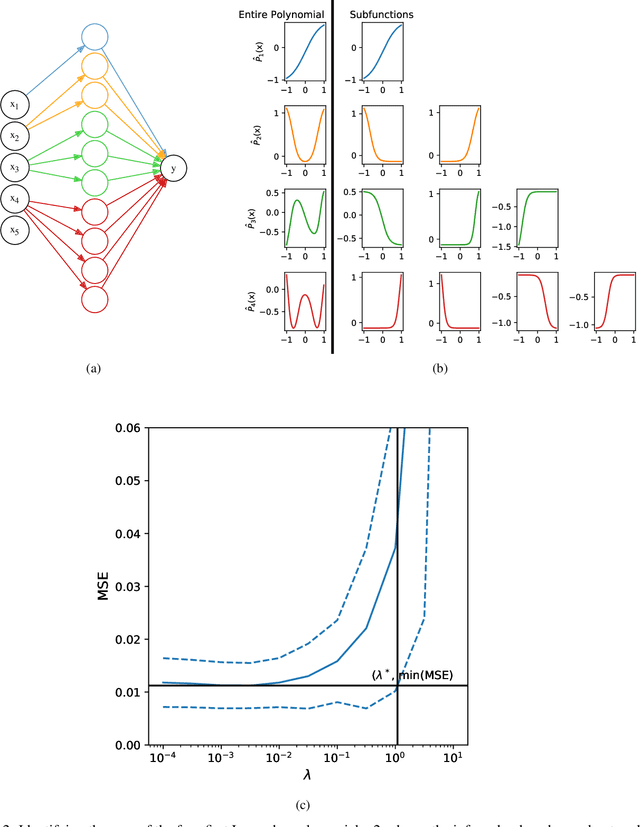
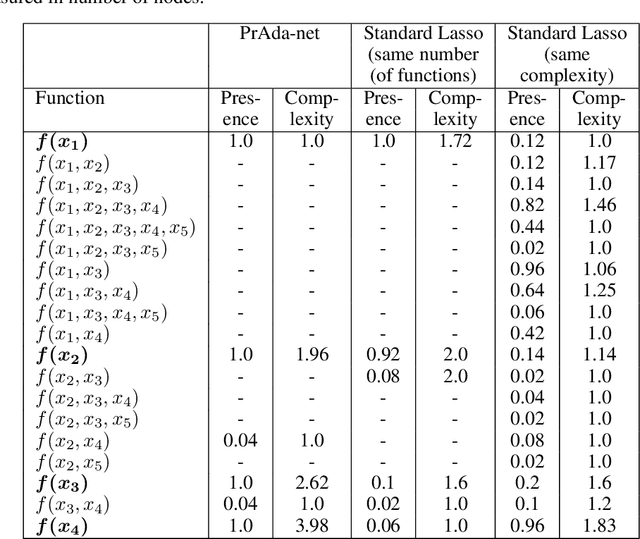
Neural networks excel in terms of predictive performance, with little or no need for manual screening of variables or guided definition of network architecture. However, these flexible and data adaptive models are often difficult to interpret. Here, we propose a new method for enhancing interpretability, that builds on proximal gradient descent and adaptive lasso, PrAda-net. In contrast to other lasso-based algorithms, PrAda-net penalizes all network links individually and, by removing links with smaller weights, automatically adjusts the size of the neural network to capture the complexity of the underlying data generative model, thus increasing interpretability. In addition, the compact network obtained by PrAda-net can be used to identify relevant dependencies in the data, making it suitable for non-parametric statistical modelling with automatic model selection. We demonstrate PrAda-net on simulated data, where we compare the test error performance, variable importance and variable subset identification properties of PrAda-net to other lasso-based approaches. We also apply Prada-net to the massive U.K.\ black smoke data set, to demonstrate the capability of using Prada-net as an alternative to generalized additive models (GAMs), which often require domain knowledge to select the functional forms of the additive components. Prada-net, in contrast, requires no such pre-selection while still resulting in interpretable additive components.