Controlled Descent Training

In this work, a novel and model-based artificial neural network (ANN) training method is developed supported by optimal control theory. The method augments training labels in order to robustly guarantee training loss convergence and improve training convergence rate. Dynamic label augmentation is proposed within the framework of gradient descent training where the convergence of training loss is controlled. First, we capture the training behavior with the help of empirical Neural Tangent Kernels (NTK) and borrow tools from systems and control theory to analyze both the local and global training dynamics (e.g. stability, reachability). Second, we propose to dynamically alter the gradient descent training mechanism via fictitious labels as control inputs and an optimal state feedback policy. In this way, we enforce locally $\mathcal{H}_2$ optimal and convergent training behavior. The novel algorithm, \textit{Controlled Descent Training} (CDT), guarantees local convergence. CDT unleashes new potentials in the analysis, interpretation, and design of ANN architectures. The applicability of the method is demonstrated on standard regression and classification problems.

Deep Q-learning: a robust control approach

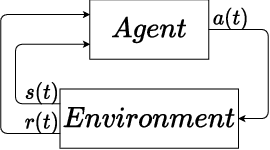
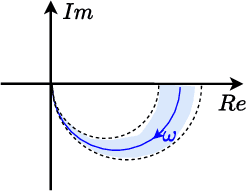
In this paper, we place deep Q-learning into a control-oriented perspective and study its learning dynamics with well-established techniques from robust control. We formulate an uncertain linear time-invariant model by means of the neural tangent kernel to describe learning. We show the instability of learning and analyze the agent's behavior in frequency-domain. Then, we ensure convergence via robust controllers acting as dynamical rewards in the loss function. We synthesize three controllers: state-feedback gain scheduling $\mathcal{H}_2$, dynamic $\mathcal{H}_\infty$, and constant gain $\mathcal{H}_\infty$ controllers. Setting up the learning agent with a control-oriented tuning methodology is more transparent and has well-established literature compared to the heuristics in reinforcement learning. In addition, our approach does not use a target network and randomized replay memory. The role of the target network is overtaken by the control input, which also exploits the temporal dependency of samples (opposed to a randomized memory buffer). Numerical simulations in different OpenAI Gym environments suggest that the $\mathcal{H}_\infty$ controlled learning performs slightly better than Double deep Q-learning.

Constrained Policy Gradient Method for Safe and Fast Reinforcement Learning: a Neural Tangent Kernel Based Approach

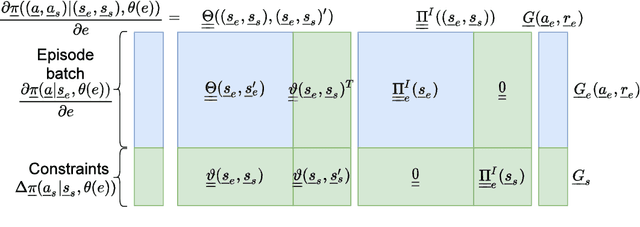
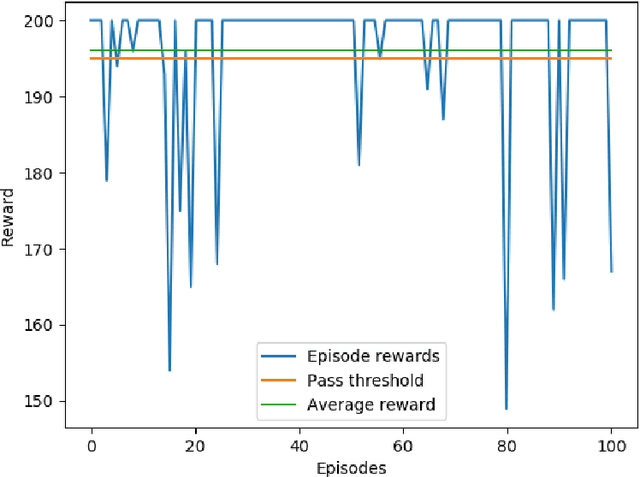
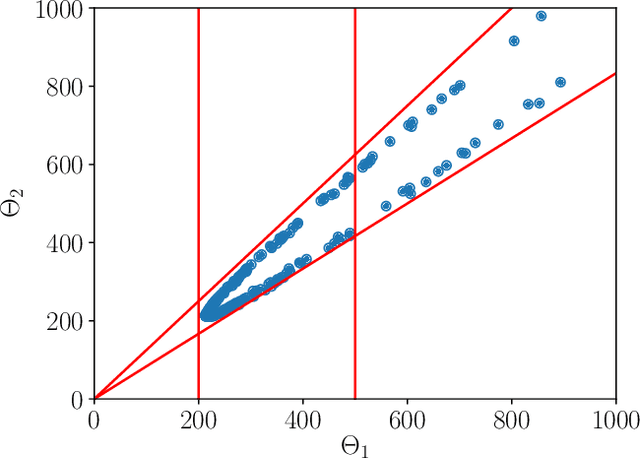
This paper presents a constrained policy gradient algorithm. We introduce constraints for safe learning with the following steps. First, learning is slowed down (lazy learning) so that the episodic policy change can be computed with the help of the policy gradient theorem and the neural tangent kernel. Then, this enables us the evaluation of the policy at arbitrary states too. In the same spirit, learning can be guided, ensuring safety via augmenting episode batches with states where the desired action probabilities are prescribed. Finally, exogenous discounted sum of future rewards (returns) can be computed at these specific state-action pairs such that the policy network satisfies constraints. Computing the returns is based on solving a system of linear equations (equality constraints) or a constrained quadratic program (inequality constraints). Simulation results suggest that adding constraints (external information) to the learning can improve learning in terms of speed and safety reasonably if constraints are appropriately selected. The efficiency of the constrained learning was demonstrated with a shallow and wide ReLU network in the Cartpole and Lunar Lander OpenAI gym environments. The main novelty of the paper is giving a practical use of the neural tangent kernel in reinforcement learning.