Deep Q-learning: a robust control approach

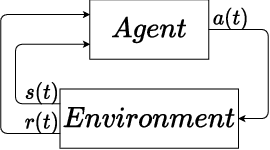
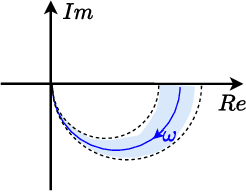
In this paper, we place deep Q-learning into a control-oriented perspective and study its learning dynamics with well-established techniques from robust control. We formulate an uncertain linear time-invariant model by means of the neural tangent kernel to describe learning. We show the instability of learning and analyze the agent's behavior in frequency-domain. Then, we ensure convergence via robust controllers acting as dynamical rewards in the loss function. We synthesize three controllers: state-feedback gain scheduling $\mathcal{H}_2$, dynamic $\mathcal{H}_\infty$, and constant gain $\mathcal{H}_\infty$ controllers. Setting up the learning agent with a control-oriented tuning methodology is more transparent and has well-established literature compared to the heuristics in reinforcement learning. In addition, our approach does not use a target network and randomized replay memory. The role of the target network is overtaken by the control input, which also exploits the temporal dependency of samples (opposed to a randomized memory buffer). Numerical simulations in different OpenAI Gym environments suggest that the $\mathcal{H}_\infty$ controlled learning performs slightly better than Double deep Q-learning.