Vincent Szolnoky
Controlled Descent Training
Mar 16, 2023Abstract:In this work, a novel and model-based artificial neural network (ANN) training method is developed supported by optimal control theory. The method augments training labels in order to robustly guarantee training loss convergence and improve training convergence rate. Dynamic label augmentation is proposed within the framework of gradient descent training where the convergence of training loss is controlled. First, we capture the training behavior with the help of empirical Neural Tangent Kernels (NTK) and borrow tools from systems and control theory to analyze both the local and global training dynamics (e.g. stability, reachability). Second, we propose to dynamically alter the gradient descent training mechanism via fictitious labels as control inputs and an optimal state feedback policy. In this way, we enforce locally $\mathcal{H}_2$ optimal and convergent training behavior. The novel algorithm, \textit{Controlled Descent Training} (CDT), guarantees local convergence. CDT unleashes new potentials in the analysis, interpretation, and design of ANN architectures. The applicability of the method is demonstrated on standard regression and classification problems.
On the Interpretability of Regularisation for Neural Networks Through Model Gradient Similarity
May 25, 2022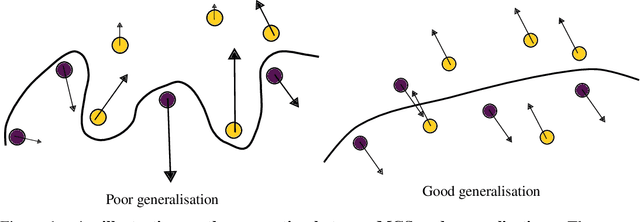

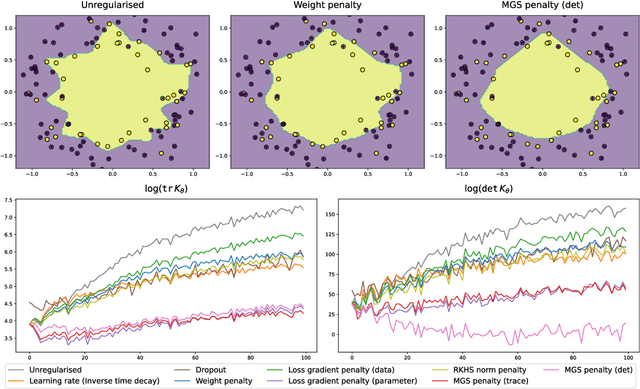
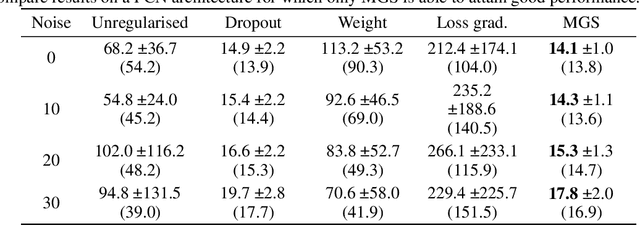
Abstract:Most complex machine learning and modelling techniques are prone to over-fitting and may subsequently generalise poorly to future data. Artificial neural networks are no different in this regard and, despite having a level of implicit regularisation when trained with gradient descent, often require the aid of explicit regularisers. We introduce a new framework, Model Gradient Similarity (MGS), that (1) serves as a metric of regularisation, which can be used to monitor neural network training, (2) adds insight into how explicit regularisers, while derived from widely different principles, operate via the same mechanism underneath by increasing MGS, and (3) provides the basis for a new regularisation scheme which exhibits excellent performance, especially in challenging settings such as high levels of label noise or limited sample sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge