Constrained Policy Gradient Method for Safe and Fast Reinforcement Learning: a Neural Tangent Kernel Based Approach

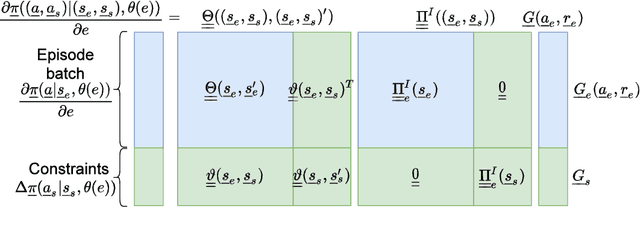
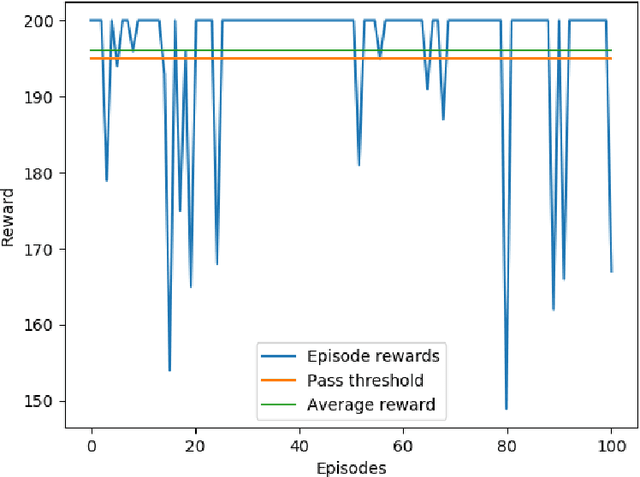
This paper presents a constrained policy gradient algorithm. We introduce constraints for safe learning with the following steps. First, learning is slowed down (lazy learning) so that the episodic policy change can be computed with the help of the policy gradient theorem and the neural tangent kernel. Then, this enables us the evaluation of the policy at arbitrary states too. In the same spirit, learning can be guided, ensuring safety via augmenting episode batches with states where the desired action probabilities are prescribed. Finally, exogenous discounted sum of future rewards (returns) can be computed at these specific state-action pairs such that the policy network satisfies constraints. Computing the returns is based on solving a system of linear equations (equality constraints) or a constrained quadratic program (inequality constraints). Simulation results suggest that adding constraints (external information) to the learning can improve learning in terms of speed and safety reasonably if constraints are appropriately selected. The efficiency of the constrained learning was demonstrated with a shallow and wide ReLU network in the Cartpole and Lunar Lander OpenAI gym environments. The main novelty of the paper is giving a practical use of the neural tangent kernel in reinforcement learning.