Bandwidth Selection for Gaussian Kernel Ridge Regression via Jacobian Control

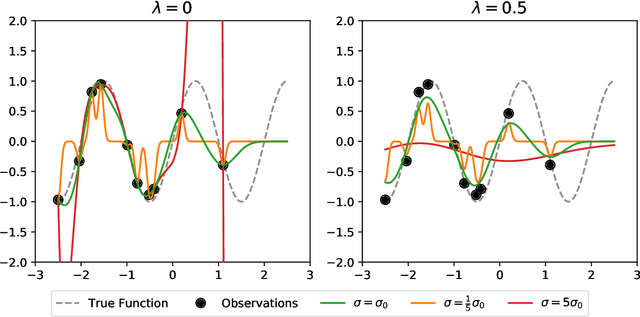
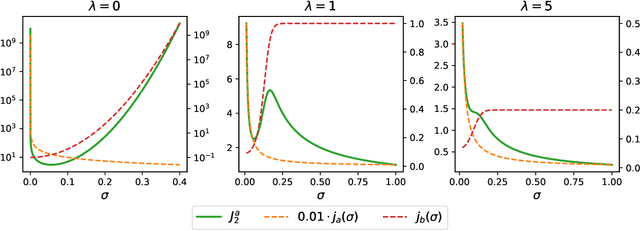
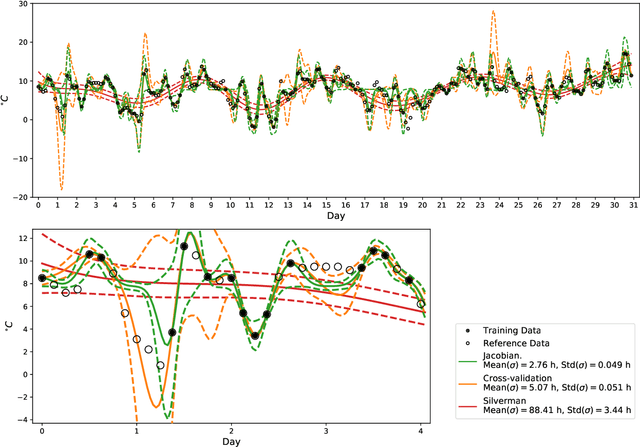
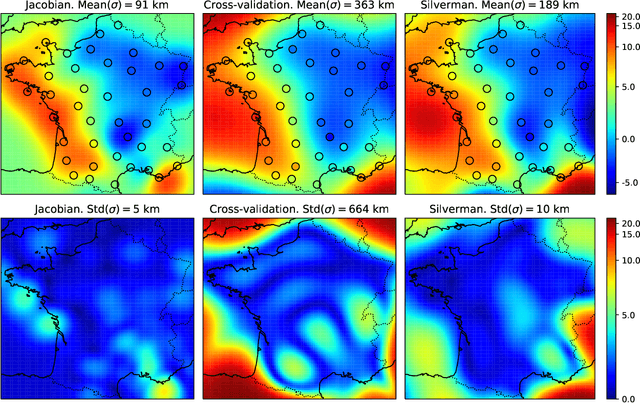
Most machine learning methods depend on the tuning of hyper-parameters. For kernel ridge regression (KRR) with the Gaussian kernel, the hyper-parameter is the bandwidth. The bandwidth specifies the length-scale of the kernel and has to be carefully selected in order to obtain a model with good generalization. The default method for bandwidth selection is cross-validation, which often yields good results, albeit at high computational costs. Furthermore, the estimates provided by cross-validation tend to have very high variance, especially when training data are scarce. Inspired by Jacobian regularization, we formulate how the derivatives of the functions inferred by KRR with the Gaussian kernel depend on the kernel bandwidth. We then use this expression to propose a closed-form, computationally feather-light, bandwidth selection method based on controlling the Jacobian. In addition, the Jacobian expression illuminates how the bandwidth selection is a trade-off between the smoothness of the inferred function, and the conditioning of the training data kernel matrix. We show on real and synthetic data that compared to cross-validation, our method is considerably more stable in terms of bandwidth selection, and, for small data sets, provides better predictions.