Supervised Models Can Generalize Also When Trained on Random Label

The success of unsupervised learning raises the question of whether also supervised models can be trained without using the information in the output $y$. In this paper, we demonstrate that this is indeed possible. The key step is to formulate the model as a smoother, i.e. on the form $\hat{f}=Sy$, and to construct the smoother matrix $S$ independently of $y$, e.g. by training on random labels. We present a simple model selection criterion based on the distribution of the out-of-sample predictions and show that, in contrast to cross-validation, this criterion can be used also without access to $y$. We demonstrate on real and synthetic data that $y$-free trained versions of linear and kernel ridge regression, smoothing splines, and neural networks perform similarly to their standard, $y$-based, versions and, most importantly, significantly better than random guessing.

Solving Kernel Ridge Regression with Gradient Descent for a Non-Constant Kernel

Kernel ridge regression, KRR, is a generalization of linear ridge regression that is non-linear in the data, but linear in the parameters. The solution can be obtained either as a closed-form solution, which includes a matrix inversion, or iteratively through gradient descent. Using the iterative approach opens up for changing the kernel during training, something that is investigated in this paper. We theoretically address the effects this has on model complexity and generalization. Based on our findings, we propose an update scheme for the bandwidth of translational-invariant kernels, where we let the bandwidth decrease to zero during training, thus circumventing the need for hyper-parameter selection. We demonstrate on real and synthetic data how decreasing the bandwidth during training outperforms using a constant bandwidth, selected by cross-validation and marginal likelihood maximization. We also show theoretically and empirically that using a decreasing bandwidth, we are able to achieve both zero training error in combination with good generalization, and a double descent behavior, phenomena that do not occur for KRR with constant bandwidth but are known to appear for neural networks.

Solving Kernel Ridge Regression with Gradient-Based Optimization Methods

Kernel ridge regression, KRR, is a non-linear generalization of linear ridge regression. Here, we introduce an equivalent formulation of the objective function of KRR, opening up both for using other penalties than the ridge penalty and for studying kernel ridge regression from the perspective of gradient descent. Using a continuous-time perspective, we derive a closed-form solution, kernel gradient flow, KGF, with regularization through early stopping, which allows us to theoretically bound the differences between KGF and KRR. We generalize KRR by replacing the ridge penalty with the $\ell_1$ and $\ell_\infty$ penalties and utilize the fact that analogously to the similarities between KGF and KRR, the solutions obtained when using these penalties are very similar to those obtained from forward stagewise regression (also known as coordinate descent) and sign gradient descent in combination with early stopping. Thus the need for computationally heavy proximal gradient descent algorithms can be alleviated. We show theoretically and empirically how these penalties, and corresponding gradient-based optimization algorithms, produce signal-driven and robust regression solutions, respectively. We also investigate kernel gradient descent where the kernel is allowed to change during training, and theoretically address the effects this has on generalization. Based on our findings, we propose an update scheme for the bandwidth of translational-invariant kernels, where we let the bandwidth decrease to zero during training, thus circumventing the need for hyper-parameter selection. We demonstrate on real and synthetic data how decreasing the bandwidth during training outperforms using a constant bandwidth, selected by cross-validation and marginal likelihood maximization. We also show that using a decreasing bandwidth, we are able to achieve both zero training error and a double descent behavior.

Bandwidth Selection for Gaussian Kernel Ridge Regression via Jacobian Control

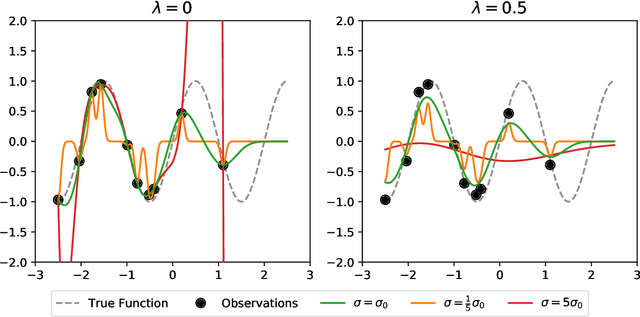
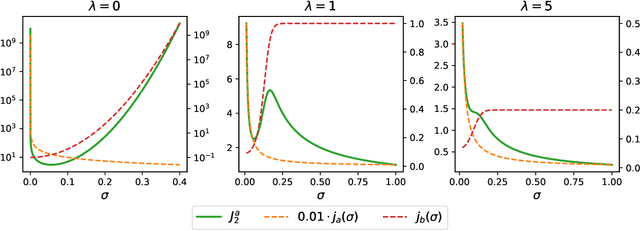
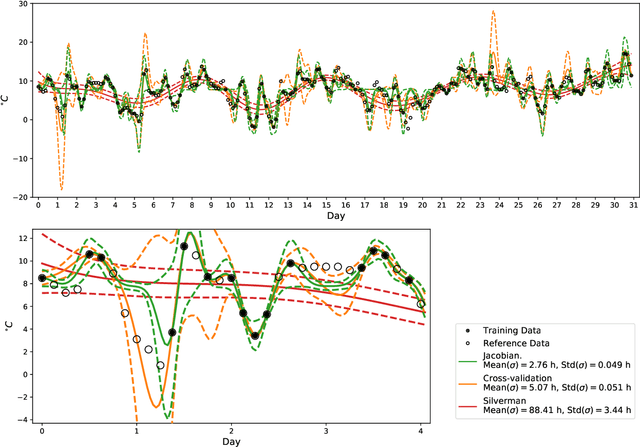
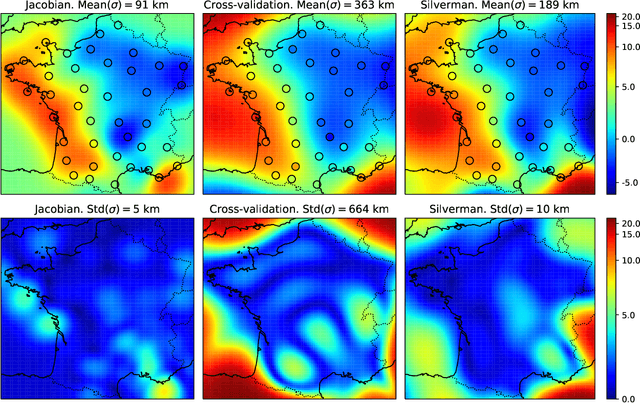
Most machine learning methods depend on the tuning of hyper-parameters. For kernel ridge regression (KRR) with the Gaussian kernel, the hyper-parameter is the bandwidth. The bandwidth specifies the length-scale of the kernel and has to be carefully selected in order to obtain a model with good generalization. The default method for bandwidth selection is cross-validation, which often yields good results, albeit at high computational costs. Furthermore, the estimates provided by cross-validation tend to have very high variance, especially when training data are scarce. Inspired by Jacobian regularization, we formulate how the derivatives of the functions inferred by KRR with the Gaussian kernel depend on the kernel bandwidth. We then use this expression to propose a closed-form, computationally feather-light, bandwidth selection method based on controlling the Jacobian. In addition, the Jacobian expression illuminates how the bandwidth selection is a trade-off between the smoothness of the inferred function, and the conditioning of the training data kernel matrix. We show on real and synthetic data that compared to cross-validation, our method is considerably more stable in terms of bandwidth selection, and, for small data sets, provides better predictions.

Non-linear, Sparse Dimensionality Reduction via Path Lasso Penalized Autoencoders

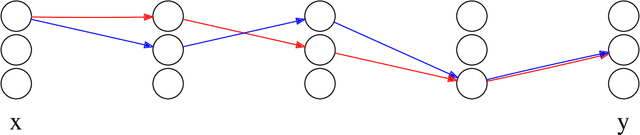
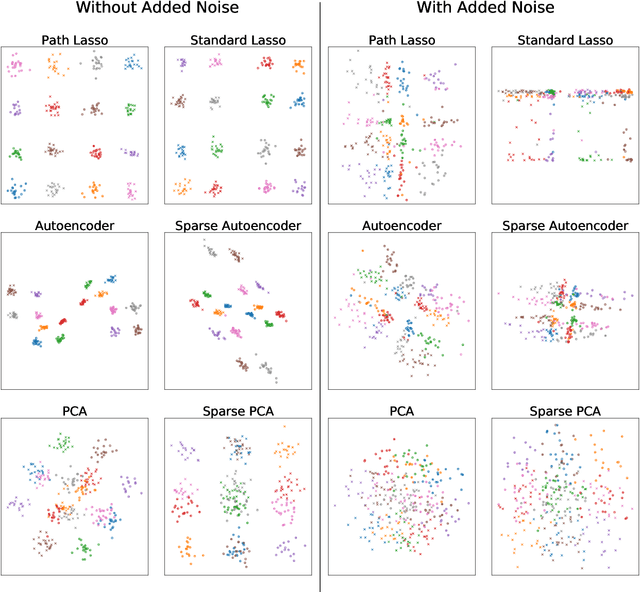
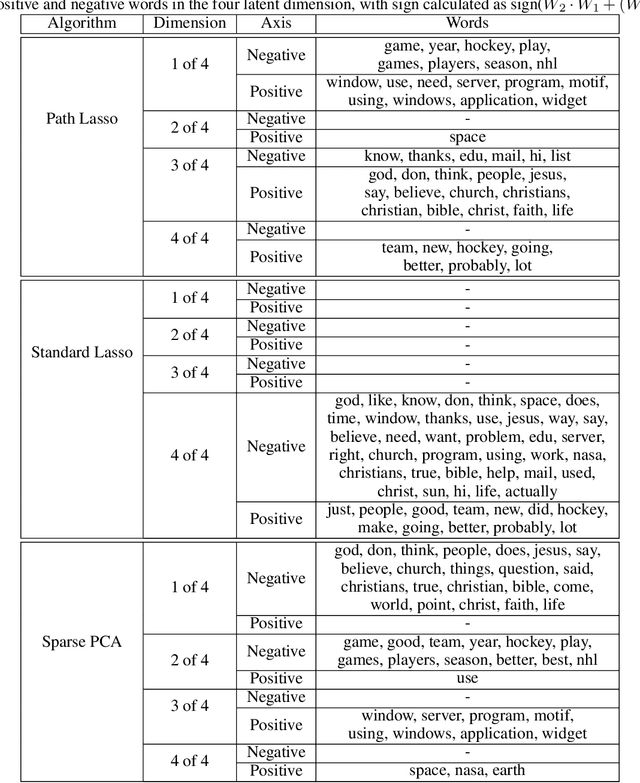
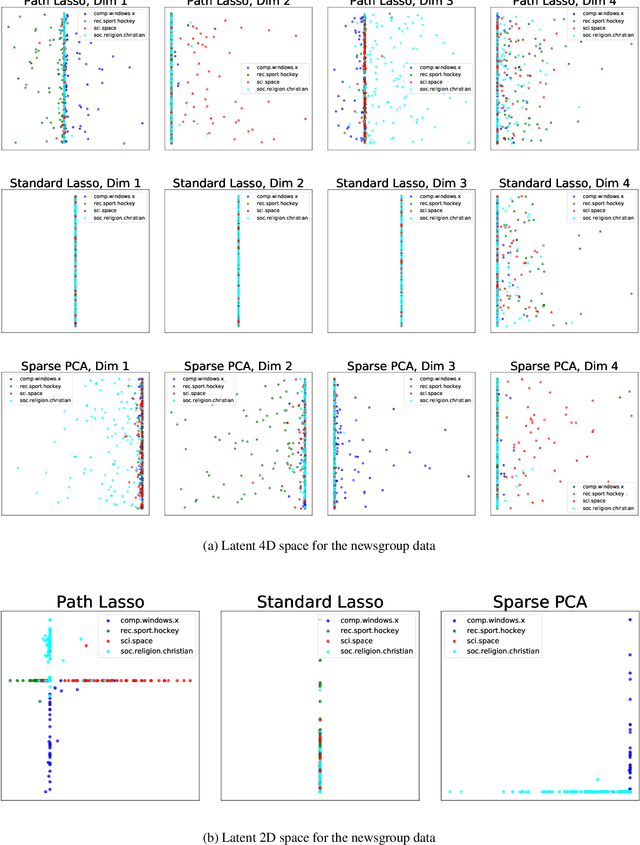
High-dimensional data sets are often analyzed and explored via the construction of a latent low-dimensional space which enables convenient visualization and efficient predictive modeling or clustering. For complex data structures, linear dimensionality reduction techniques like PCA may not be sufficiently flexible to enable low-dimensional representation. Non-linear dimension reduction techniques, like kernel PCA and autoencoders, suffer from loss of interpretability since each latent variable is dependent of all input dimensions. To address this limitation, we here present path lasso penalized autoencoders. This structured regularization enhances interpretability by penalizing each path through the encoder from an input to a latent variable, thus restricting how many input variables are represented in each latent dimension. Our algorithm uses a group lasso penalty and non-negative matrix factorization to construct a sparse, non-linear latent representation. We compare the path lasso regularized autoencoder to PCA, sparse PCA, autoencoders and sparse autoencoders on real and simulated data sets. We show that the algorithm exhibits much lower reconstruction errors than sparse PCA and parameter-wise lasso regularized autoencoders for low-dimensional representations. Moreover, path lasso representations provide a more accurate reconstruction match, i.e. preserved relative distance between objects in the original and reconstructed spaces.

Flexible, Non-parametric Modeling Using Regularized Neural Networks

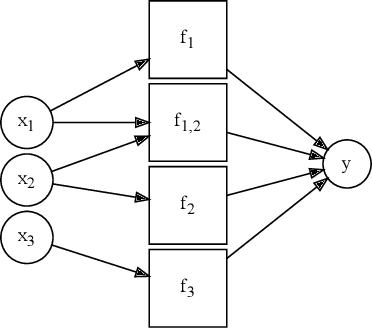
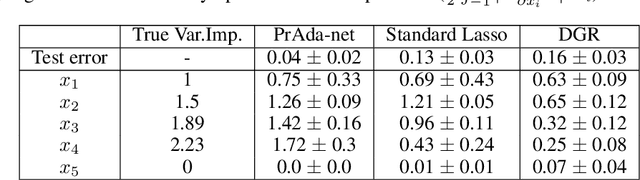
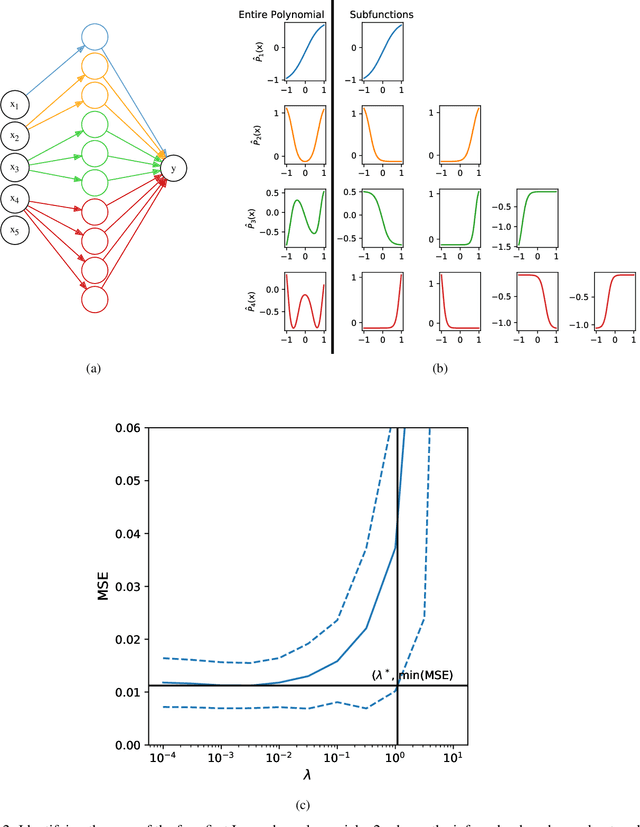
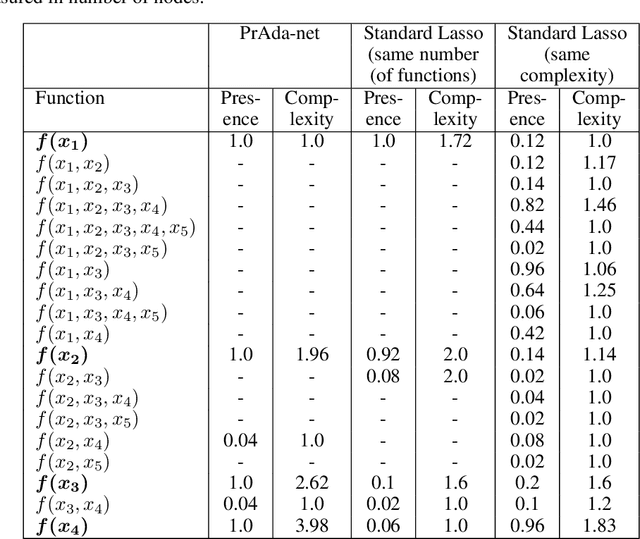
Neural networks excel in terms of predictive performance, with little or no need for manual screening of variables or guided definition of network architecture. However, these flexible and data adaptive models are often difficult to interpret. Here, we propose a new method for enhancing interpretability, that builds on proximal gradient descent and adaptive lasso, PrAda-net. In contrast to other lasso-based algorithms, PrAda-net penalizes all network links individually and, by removing links with smaller weights, automatically adjusts the size of the neural network to capture the complexity of the underlying data generative model, thus increasing interpretability. In addition, the compact network obtained by PrAda-net can be used to identify relevant dependencies in the data, making it suitable for non-parametric statistical modelling with automatic model selection. We demonstrate PrAda-net on simulated data, where we compare the test error performance, variable importance and variable subset identification properties of PrAda-net to other lasso-based approaches. We also apply Prada-net to the massive U.K.\ black smoke data set, to demonstrate the capability of using Prada-net as an alternative to generalized additive models (GAMs), which often require domain knowledge to select the functional forms of the additive components. Prada-net, in contrast, requires no such pre-selection while still resulting in interpretable additive components.