Partial Distribution Matching via Partial Wasserstein Adversarial Networks

This paper studies the problem of distribution matching (DM), which is a fundamental machine learning problem seeking to robustly align two probability distributions. Our approach is established on a relaxed formulation, called partial distribution matching (PDM), which seeks to match a fraction of the distributions instead of matching them completely. We theoretically derive the Kantorovich-Rubinstein duality for the partial Wasserstain-1 (PW) discrepancy, and develop a partial Wasserstein adversarial network (PWAN) that efficiently approximates the PW discrepancy based on this dual form. Partial matching can then be achieved by optimizing the network using gradient descent. Two practical tasks, point set registration and partial domain adaptation are investigated, where the goals are to partially match distributions in 3D space and high-dimensional feature space respectively. The experiment results confirm that the proposed PWAN effectively produces highly robust matching results, performing better or on par with the state-of-the-art methods.

Partial Wasserstein Adversarial Network for Non-rigid Point Set Registration

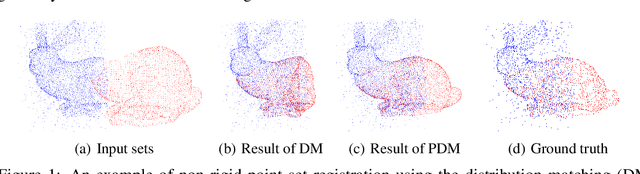
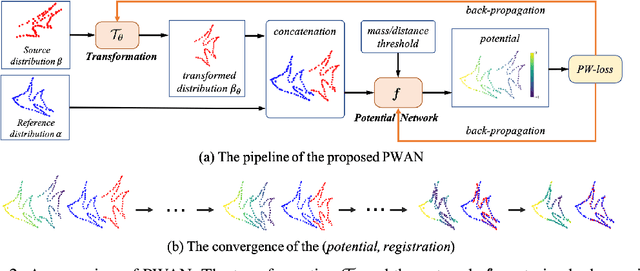
Given two point sets, the problem of registration is to recover a transformation that matches one set to the other. This task is challenging due to the presence of the large number of outliers, the unknown non-rigid deformations and the large sizes of point sets. To obtain strong robustness against outliers, we formulate the registration problem as a partial distribution matching (PDM) problem, where the goal is to partially match the distributions represented by point sets in a metric space. To handle large point sets, we propose a scalable PDM algorithm by utilizing the efficient partial Wasserstein-1 (PW) discrepancy. Specifically, we derive the Kantorovich-Rubinstein duality for the PW discrepancy, and show its gradient can be explicitly computed. Based on these results, we propose a partial Wasserstein adversarial network (PWAN), which is able to approximate the PW discrepancy by a neural network, and minimize it by gradient descent. In addition, it also incorporates an efficient coherence regularizer for non-rigid transformations to avoid unrealistic deformations. We evaluate PWAN on practical point set registration tasks, and show that the proposed PWAN is robust, scalable and performs more favorably than the state-of-the-art methods.