KeyGS: A Keyframe-Centric Gaussian Splatting Method for Monocular Image Sequences

Reconstructing high-quality 3D models from sparse 2D images has garnered significant attention in computer vision. Recently, 3D Gaussian Splatting (3DGS) has gained prominence due to its explicit representation with efficient training speed and real-time rendering capabilities. However, existing methods still heavily depend on accurate camera poses for reconstruction. Although some recent approaches attempt to train 3DGS models without the Structure-from-Motion (SfM) preprocessing from monocular video datasets, these methods suffer from prolonged training times, making them impractical for many applications. In this paper, we present an efficient framework that operates without any depth or matching model. Our approach initially uses SfM to quickly obtain rough camera poses within seconds, and then refines these poses by leveraging the dense representation in 3DGS. This framework effectively addresses the issue of long training times. Additionally, we integrate the densification process with joint refinement and propose a coarse-to-fine frequency-aware densification to reconstruct different levels of details. This approach prevents camera pose estimation from being trapped in local minima or drifting due to high-frequency signals. Our method significantly reduces training time from hours to minutes while achieving more accurate novel view synthesis and camera pose estimation compared to previous methods.

Partial Distribution Matching via Partial Wasserstein Adversarial Networks

This paper studies the problem of distribution matching (DM), which is a fundamental machine learning problem seeking to robustly align two probability distributions. Our approach is established on a relaxed formulation, called partial distribution matching (PDM), which seeks to match a fraction of the distributions instead of matching them completely. We theoretically derive the Kantorovich-Rubinstein duality for the partial Wasserstain-1 (PW) discrepancy, and develop a partial Wasserstein adversarial network (PWAN) that efficiently approximates the PW discrepancy based on this dual form. Partial matching can then be achieved by optimizing the network using gradient descent. Two practical tasks, point set registration and partial domain adaptation are investigated, where the goals are to partially match distributions in 3D space and high-dimensional feature space respectively. The experiment results confirm that the proposed PWAN effectively produces highly robust matching results, performing better or on par with the state-of-the-art methods.

Partial Wasserstein Adversarial Network for Non-rigid Point Set Registration

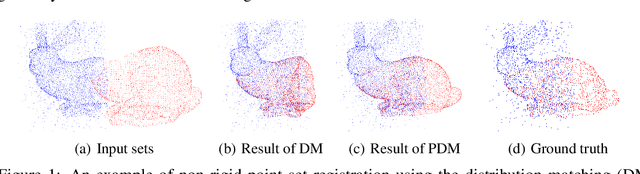
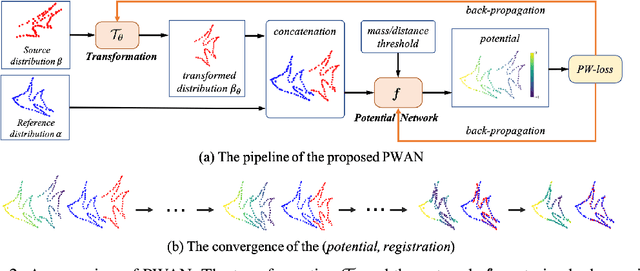
Given two point sets, the problem of registration is to recover a transformation that matches one set to the other. This task is challenging due to the presence of the large number of outliers, the unknown non-rigid deformations and the large sizes of point sets. To obtain strong robustness against outliers, we formulate the registration problem as a partial distribution matching (PDM) problem, where the goal is to partially match the distributions represented by point sets in a metric space. To handle large point sets, we propose a scalable PDM algorithm by utilizing the efficient partial Wasserstein-1 (PW) discrepancy. Specifically, we derive the Kantorovich-Rubinstein duality for the PW discrepancy, and show its gradient can be explicitly computed. Based on these results, we propose a partial Wasserstein adversarial network (PWAN), which is able to approximate the PW discrepancy by a neural network, and minimize it by gradient descent. In addition, it also incorporates an efficient coherence regularizer for non-rigid transformations to avoid unrealistic deformations. We evaluate PWAN on practical point set registration tasks, and show that the proposed PWAN is robust, scalable and performs more favorably than the state-of-the-art methods.

Conditional Generative ConvNets for Exemplar-based Texture Synthesis

The goal of exemplar-based texture synthesis is to generate texture images that are visually similar to a given exemplar. Recently, promising results have been reported by methods relying on convolutional neural networks (ConvNets) pretrained on large-scale image datasets. However, these methods have difficulties in synthesizing image textures with non-local structures and extending to dynamic or sound textures. In this paper, we present a conditional generative ConvNet (cgCNN) model which combines deep statistics and the probabilistic framework of generative ConvNet (gCNN) model. Given a texture exemplar, the cgCNN model defines a conditional distribution using deep statistics of a ConvNet, and synthesize new textures by sampling from the conditional distribution. In contrast to previous deep texture models, the proposed cgCNN dose not rely on pre-trained ConvNets but learns the weights of ConvNets for each input exemplar instead. As a result, the cgCNN model can synthesize high quality dynamic, sound and image textures in a unified manner. We also explore the theoretical connections between our model and other texture models. Further investigations show that the cgCNN model can be easily generalized to texture expansion and inpainting. Extensive experiments demonstrate that our model can achieve better or at least comparable results than the state-of-the-art methods.

Texture Mixing by Interpolating Deep Statistics via Gaussian Models

Recently, enthusiastic studies have devoted to texture synthesis using deep neural networks, because these networks excel at handling complex patterns in images. In these models, second-order statistics, such as Gram matrix, are used to describe textures. Despite the fact that these model have achieved promising results, the structure of their parametric space is still unclear, consequently, it is difficult to use them to mix textures. This paper addresses the texture mixing problem by using a Gaussian scheme to interpolate deep statistics computed from deep neural networks. More precisely, we first reveal that the statistics used in existing deep models can be unified using a stationary Gaussian scheme. We then present a novel algorithm to mix these statistics by interpolating between Gaussian models using optimal transport. We further apply our scheme to Neural Style Transfer, where we can create mixed styles. The experiments demonstrate that our method can achieve state-of-the-art results. Because all the computations are implemented in closed forms, our mixing algorithm adds only negligible time to the original texture synthesis procedure.