SE(3)-bi-equivariant Transformers for Point Cloud Assembly
Paper and Code
Jul 12, 2024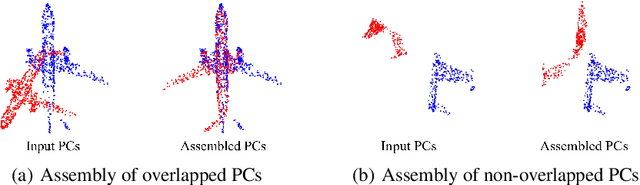

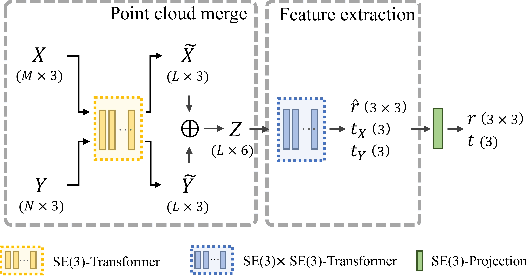
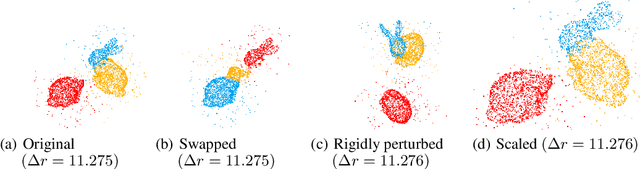
Given a pair of point clouds, the goal of assembly is to recover a rigid transformation that aligns one point cloud to the other. This task is challenging because the point clouds may be non-overlapped, and they may have arbitrary initial positions. To address these difficulties, we propose a method, called SE(3)-bi-equivariant transformer (BITR), based on the SE(3)-bi-equivariance prior of the task: it guarantees that when the inputs are rigidly perturbed, the output will transform accordingly. Due to its equivariance property, BITR can not only handle non-overlapped PCs, but also guarantee robustness against initial positions. Specifically, BITR first extracts features of the inputs using a novel $SE(3) \times SE(3)$-transformer, and then projects the learned feature to group SE(3) as the output. Moreover, we theoretically show that swap and scale equivariances can be incorporated into BITR, thus it further guarantees stable performance under scaling and swapping the inputs. We experimentally show the effectiveness of BITR in practical tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge