Noise Sensitivity and Stability of Deep Neural Networks for Binary Classification

A first step is taken towards understanding often observed non-robustness phenomena of deep neural net (DNN) classifiers. This is done from the perspective of Boolean functions by asking if certain sequences of Boolean functions represented by common DNN models are noise sensitive or noise stable, concepts defined in the Boolean function literature. Due to the natural randomness in DNN models, these concepts are extended to annealed and quenched versions. Here we sort out the relation between these definitions and investigate the properties of two standard DNN architectures, the fully connected and convolutional models, when initiated with Gaussian weights.

Robust Neural Network Classification via Double Regularization

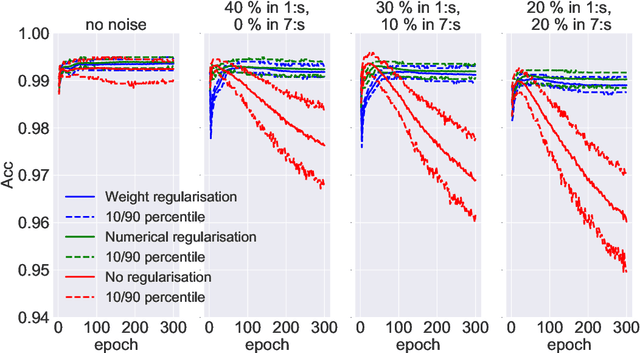
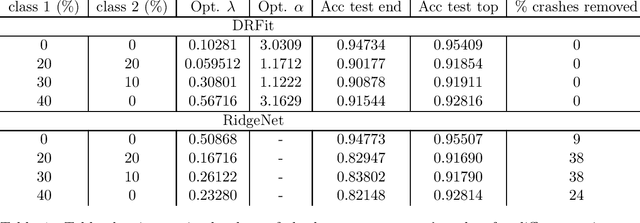
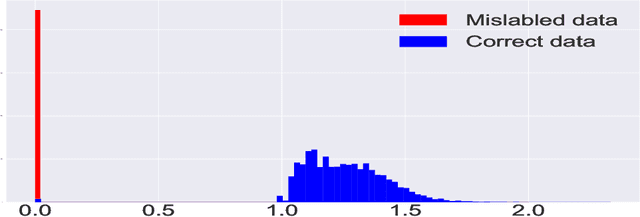
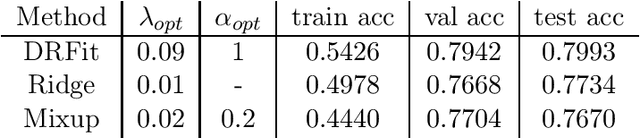
The presence of mislabeled observations in data is a notoriously challenging problem in statistics and machine learning, associated with poor generalization properties for both traditional classifiers and, perhaps even more so, flexible classifiers like neural networks. Here we propose a novel double regularization of the neural network training loss that combines a penalty on the complexity of the classification model and an optimal reweighting of training observations. The combined penalties result in improved generalization properties and strong robustness against overfitting in different settings of mislabeled training data and also against variation in initial parameter values when training. We provide a theoretical justification for our proposed method derived for a simple case of logistic regression. We demonstrate the double regularization model, here denoted by DRFit, for neural net classification of (i) MNIST and (ii) CIFAR-10, in both cases with simulated mislabeling. We also illustrate that DRFit identifies mislabeled data points with very good precision. This provides strong support for DRFit as a practical of-the-shelf classifier, since, without any sacrifice in performance, we get a classifier that simultaneously reduces overfitting against mislabeling and gives an accurate measure of the trustworthiness of the labels.