DiagramIR: An Automatic Pipeline for Educational Math Diagram Evaluation

Large Language Models (LLMs) are increasingly being adopted as tools for learning; however, most tools remain text-only, limiting their usefulness for domains where visualizations are essential, such as mathematics. Recent work shows that LLMs are capable of generating code that compiles to educational figures, but a major bottleneck remains: scalable evaluation of these diagrams. We address this by proposing DiagramIR: an automatic and scalable evaluation pipeline for geometric figures. Our method relies on intermediate representations (IRs) of LaTeX TikZ code. We compare our pipeline to other evaluation baselines such as LLM-as-a-Judge, showing that our approach has higher agreement with human raters. This evaluation approach also enables smaller models like GPT-4.1-Mini to perform comparably to larger models such as GPT-5 at a 10x lower inference cost, which is important for deploying accessible and scalable education technologies.

A Matter of Interest: Understanding Interestingness of Math Problems in Humans and Language Models

The evolution of mathematics has been guided in part by interestingness. From researchers choosing which problems to tackle next, to students deciding which ones to engage with, people's choices are often guided by judgments about how interesting or challenging problems are likely to be. As AI systems, such as LLMs, increasingly participate in mathematics with people -- whether for advanced research or education -- it becomes important to understand how well their judgments align with human ones. Our work examines this alignment through two empirical studies of human and LLM assessment of mathematical interestingness and difficulty, spanning a range of mathematical experience. We study two groups: participants from a crowdsourcing platform and International Math Olympiad competitors. We show that while many LLMs appear to broadly agree with human notions of interestingness, they mostly do not capture the distribution observed in human judgments. Moreover, most LLMs only somewhat align with why humans find certain math problems interesting, showing weak correlation with human-selected interestingness rationales. Together, our findings highlight both the promises and limitations of current LLMs in capturing human interestingness judgments for mathematical AI thought partnerships.

Adaptive Reinforcement Learning for Unobservable Random Delays

In standard Reinforcement Learning (RL) settings, the interaction between the agent and the environment is typically modeled as a Markov Decision Process (MDP), which assumes that the agent observes the system state instantaneously, selects an action without delay, and executes it immediately. In real-world dynamic environments, such as cyber-physical systems, this assumption often breaks down due to delays in the interaction between the agent and the system. These delays can vary stochastically over time and are typically unobservable, meaning they are unknown when deciding on an action. Existing methods deal with this uncertainty conservatively by assuming a known fixed upper bound on the delay, even if the delay is often much lower. In this work, we introduce the interaction layer, a general framework that enables agents to adaptively and seamlessly handle unobservable and time-varying delays. Specifically, the agent generates a matrix of possible future actions to handle both unpredictable delays and lost action packets sent over networks. Building on this framework, we develop a model-based algorithm, Actor-Critic with Delay Adaptation (ACDA), which dynamically adjusts to delay patterns. Our method significantly outperforms state-of-the-art approaches across a wide range of locomotion benchmark environments.

Learning Formal Mathematics From Intrinsic Motivation

How did humanity coax mathematics from the aether? We explore the Platonic view that mathematics can be discovered from its axioms - a game of conjecture and proof. We describe Minimo (Mathematics from Intrinsic Motivation): an agent that jointly learns to pose challenging problems for itself (conjecturing) and solve them (theorem proving). Given a mathematical domain axiomatized in dependent type theory, we first combine methods for constrained decoding and type-directed synthesis to sample valid conjectures from a language model. Our method guarantees well-formed conjectures by construction, even as we start with a randomly initialized model. We use the same model to represent a policy and value function for guiding proof search. Our agent targets generating hard but provable conjectures - a moving target, since its own theorem proving ability also improves as it trains. We propose novel methods for hindsight relabeling on proof search trees to significantly improve the agent's sample efficiency in both tasks. Experiments on 3 axiomatic domains (propositional logic, arithmetic and group theory) demonstrate that our agent can bootstrap from only the axioms, self-improving in generating true and challenging conjectures and in finding proofs.

Optimizing Instructions and Demonstrations for Multi-Stage Language Model Programs

Language Model Programs, i.e. sophisticated pipelines of modular language model (LM) calls, are increasingly advancing NLP tasks, but they require crafting prompts that are jointly effective for all modules. We study prompt optimization for LM programs, i.e. how to update these prompts to maximize a downstream metric without access to module-level labels or gradients. To make this tractable, we factorize our problem into optimizing the free-form instructions and few-shot demonstrations of every module and introduce several strategies to craft task-grounded instructions and navigate credit assignment across modules. Our strategies include (i) program- and data-aware techniques for proposing effective instructions, (ii) a stochastic mini-batch evaluation function for learning a surrogate model of our objective, and (iii) a meta-optimization procedure in which we refine how LMs construct proposals over time. Using these insights we develop MIPRO, a novel optimizer that outperforms baselines on five of six diverse LM programs using a best-in-class open-source model (Llama-3-8B), by as high as 12.9% accuracy. We will release our new optimizers and benchmark in DSPy at https://github.com/stanfordnlp/dspy

Scorch: A Library for Sparse Deep Learning

The rapid growth in the size of deep learning models strains the capabilities of traditional dense computation paradigms. Leveraging sparse computation has become increasingly popular for training and deploying large-scale models, but existing deep learning frameworks lack extensive support for sparse operations. To bridge this gap, we introduce Scorch, a library that seamlessly integrates efficient sparse tensor computation into the PyTorch ecosystem, with an initial focus on inference workloads on CPUs. Scorch provides a flexible and intuitive interface for sparse tensors, supporting diverse sparse data structures. Scorch introduces a compiler stack that automates key optimizations, including automatic loop ordering, tiling, and format inference. Combined with a runtime that adapts its execution to both dense and sparse data, Scorch delivers substantial speedups over hand-written PyTorch Sparse (torch.sparse) operations without sacrificing usability. More importantly, Scorch enables efficient computation of complex sparse operations that lack hand-optimized PyTorch implementations. This flexibility is crucial for exploring novel sparse architectures. We demonstrate Scorch's ease of use and performance gains on diverse deep learning models across multiple domains. With only minimal code changes, Scorch achieves 1.05-5.78x speedups over PyTorch Sparse on end-to-end tasks. Scorch's seamless integration and performance gains make it a valuable addition to the PyTorch ecosystem. We believe Scorch will enable wider exploration of sparsity as a tool for scaling deep learning and inform the development of other sparse libraries.

Delayed Sampling and Automatic Rao-Blackwellization of Probabilistic Programs

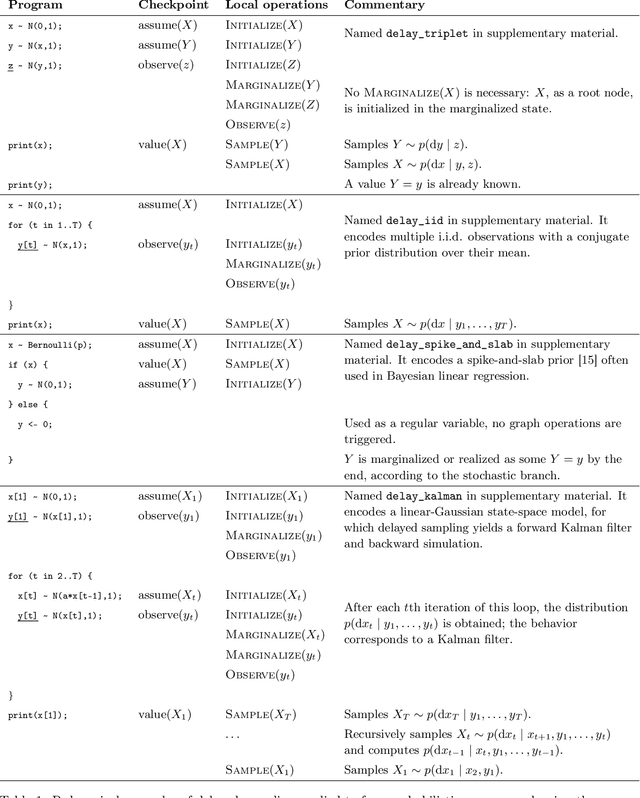
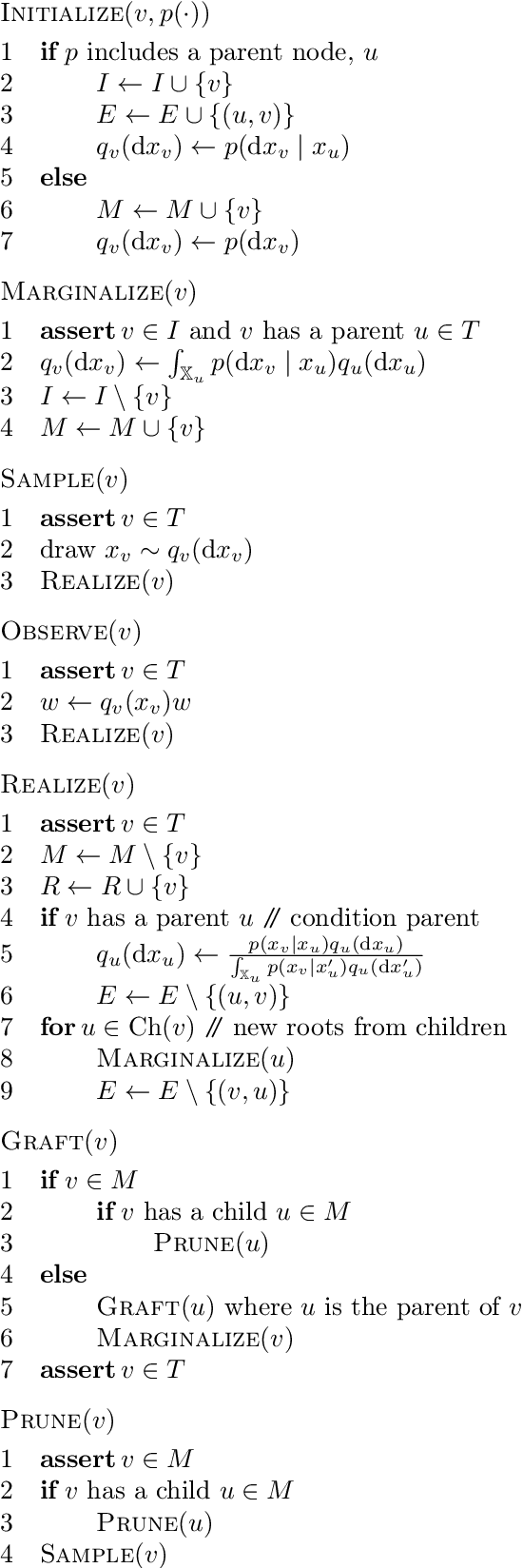
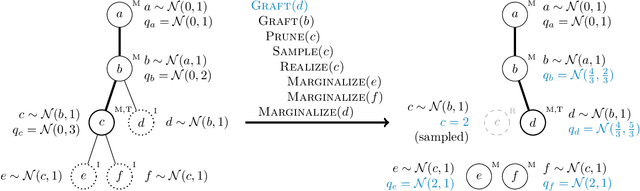
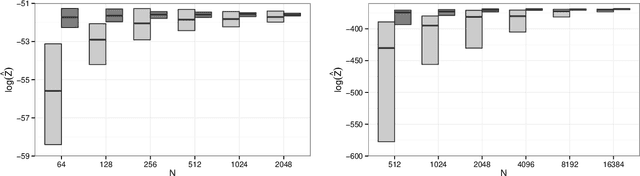
We introduce a dynamic mechanism for the solution of analytically-tractable substructure in probabilistic programs, using conjugate priors and affine transformations to reduce variance in Monte Carlo estimators. For inference with Sequential Monte Carlo, this automatically yields improvements such as locally-optimal proposals and Rao-Blackwellization. The mechanism maintains a directed graph alongside the running program that evolves dynamically as operations are triggered upon it. Nodes of the graph represent random variables, edges the analytically-tractable relationships between them. Random variables remain in the graph for as long as possible, to be sampled only when they are used by the program in a way that cannot be resolved analytically. In the meantime, they are conditioned on as many observations as possible. We demonstrate the mechanism with a few pedagogical examples, as well as a linear-nonlinear state-space model with simulated data, and an epidemiological model with real data of a dengue outbreak in Micronesia. In all cases one or more variables are automatically marginalized out to significantly reduce variance in estimates of the marginal likelihood, in the final case facilitating a random-weight or pseudo-marginal-type importance sampler for parameter estimation. We have implemented the approach in Anglican and a new probabilistic programming language called Birch.

Sparse Partially Collapsed MCMC for Parallel Inference in Topic Models

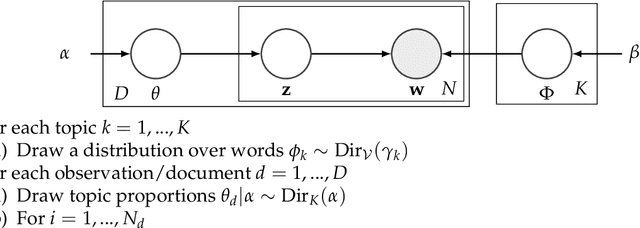
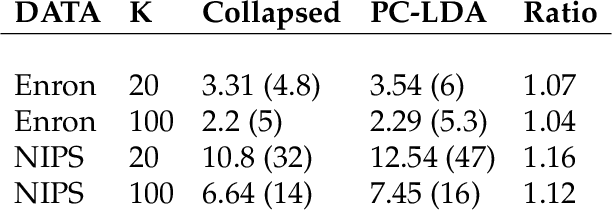
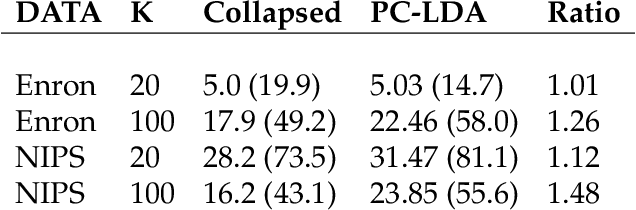
Topic models, and more specifically the class of Latent Dirichlet Allocation (LDA), are widely used for probabilistic modeling of text. MCMC sampling from the posterior distribution is typically performed using a collapsed Gibbs sampler. We propose a parallel sparse partially collapsed Gibbs sampler and compare its speed and efficiency to state-of-the-art samplers for topic models on five well-known text corpora of differing sizes and properties. In particular, we propose and compare two different strategies for sampling the parameter block with latent topic indicators. The experiments show that the increase in statistical inefficiency from only partial collapsing is smaller than commonly assumed, and can be more than compensated by the speedup from parallelization and sparsity on larger corpora. We also prove that the partially collapsed samplers scale well with the size of the corpus. The proposed algorithm is fast, efficient, exact, and can be used in more modeling situations than the ordinary collapsed sampler.