Particle filter with rejection control and unbiased estimator of the marginal likelihood

We consider the combined use of resampling and partial rejection control in sequential Monte Carlo methods, also known as particle filters. While the variance reducing properties of rejection control are known, there has not been (to the best of our knowledge) any work on unbiased estimation of the marginal likelihood (also known as the model evidence or the normalizing constant) in this type of particle filters. Being able to estimate the marginal likelihood without bias is highly relevant for model comparison, computation of interpretable and reliable confidence intervals, and in exact approximation methods, such as particle Markov chain Monte Carlo. In the paper we present a particle filter with rejection control that enables unbiased estimation of the marginal likelihood.

Probabilistic programming for birth-death models of evolution using an alive particle filter with delayed sampling

We consider probabilistic programming for birth-death models of evolution and introduce a new widely-applicable inference method that combines an extension of the alive particle filter (APF) with automatic Rao-Blackwellization via delayed sampling. Birth-death models of evolution are an important family of phylogenetic models of the diversification processes that lead to evolutionary trees. Probabilistic programming languages (PPLs) give phylogeneticists a new and exciting tool: their models can be implemented as probabilistic programs with just a basic knowledge of programming. The general inference methods in PPLs reduce the need for external experts, allow quick prototyping and testing, and accelerate the development and deployment of new models. We show how these birth-death models can be implemented as simple programs in existing PPLs, and demonstrate the usefulness of the proposed inference method for such models. For the popular BiSSE model the method yields an increase of the effective sample size and the conditional acceptance rate by a factor of 30 in comparison with a standard bootstrap particle filter. Although concentrating on phylogenetics, the extended APF is a general inference method that shows its strength in situations where particles are often assigned zero weight. In the case when the weights are always positive, the extra cost of using the APF rather than the bootstrap particle filter is negligible, making our method a suitable drop-in replacement for the bootstrap particle filter in probabilistic programming inference.

Automated learning with a probabilistic programming language: Birch

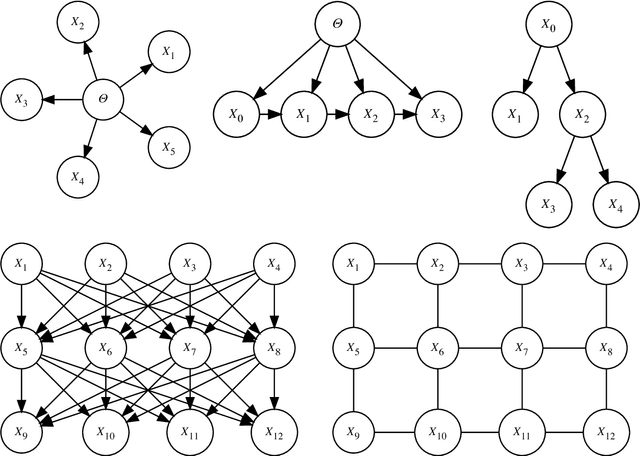
This work offers a broad perspective on probabilistic modeling and inference in light of recent advances in probabilistic programming, in which models are formally expressed in Turing-complete programming languages. We consider a typical workflow and how probabilistic programming languages can help to automate this workflow, especially in the matching of models with inference methods. We focus on two properties of a model that are critical in this matching: its structure---the conditional dependencies between random variables---and its form---the precise mathematical definition of those dependencies. While the structure and form of a probabilistic model are often fixed a priori, it is a curiosity of probabilistic programming that they need not be, and may instead vary according to random choices made during program execution. We introduce a formal description of models expressed as programs, and discuss some of the ways in which probabilistic programming languages can reveal the structure and form of these, in order to tailor inference methods. We demonstrate the ideas with a new probabilistic programming language called Birch, with a multiple object tracking example.

Delayed Sampling and Automatic Rao-Blackwellization of Probabilistic Programs

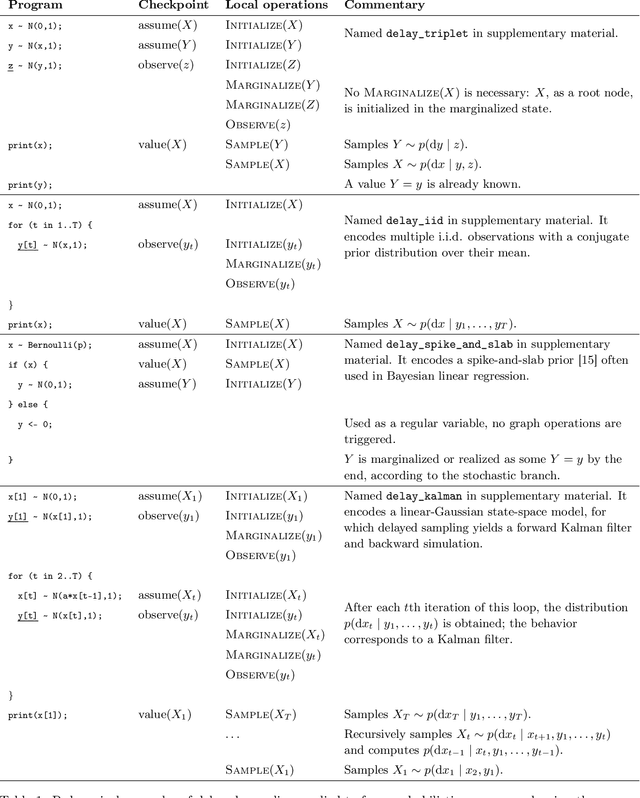
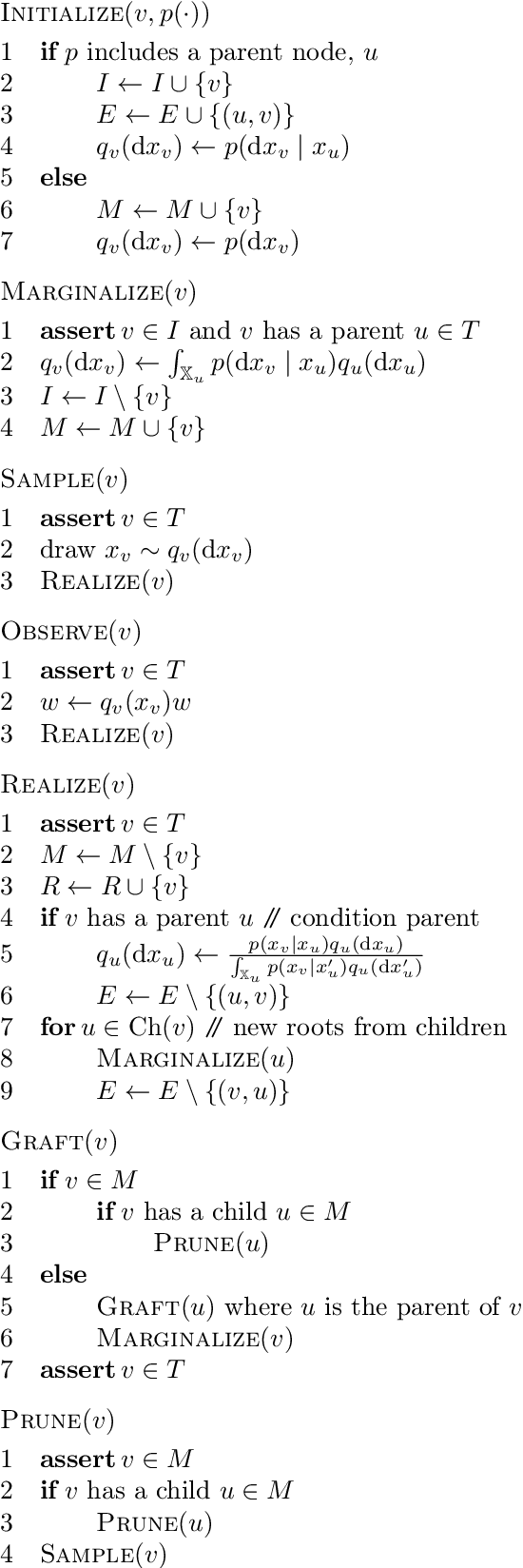
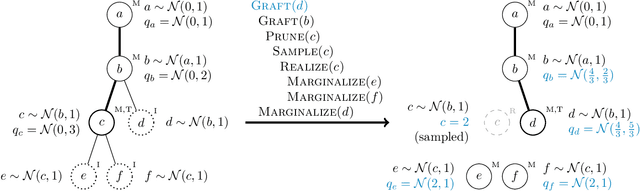
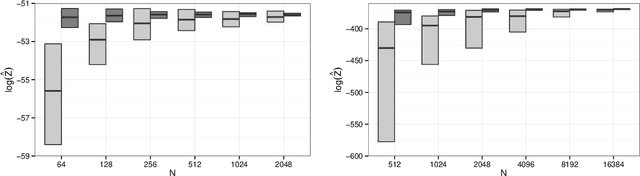
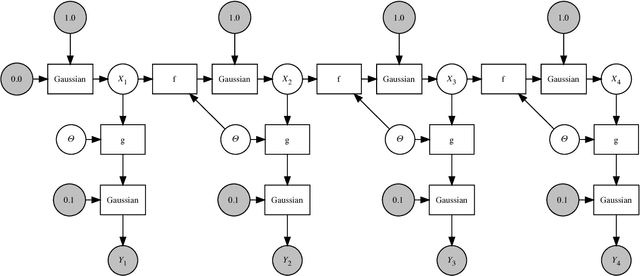
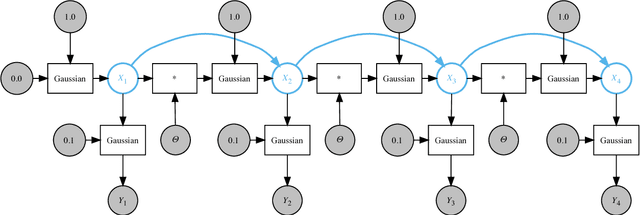
We introduce a dynamic mechanism for the solution of analytically-tractable substructure in probabilistic programs, using conjugate priors and affine transformations to reduce variance in Monte Carlo estimators. For inference with Sequential Monte Carlo, this automatically yields improvements such as locally-optimal proposals and Rao-Blackwellization. The mechanism maintains a directed graph alongside the running program that evolves dynamically as operations are triggered upon it. Nodes of the graph represent random variables, edges the analytically-tractable relationships between them. Random variables remain in the graph for as long as possible, to be sampled only when they are used by the program in a way that cannot be resolved analytically. In the meantime, they are conditioned on as many observations as possible. We demonstrate the mechanism with a few pedagogical examples, as well as a linear-nonlinear state-space model with simulated data, and an epidemiological model with real data of a dengue outbreak in Micronesia. In all cases one or more variables are automatically marginalized out to significantly reduce variance in estimates of the marginal likelihood, in the final case facilitating a random-weight or pseudo-marginal-type importance sampler for parameter estimation. We have implemented the approach in Anglican and a new probabilistic programming language called Birch.

Anytime Monte Carlo

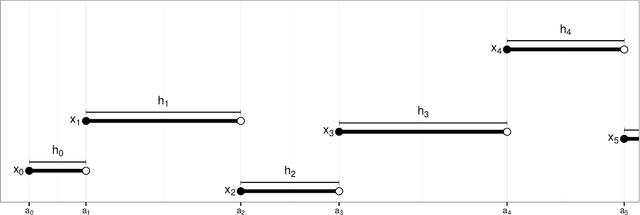
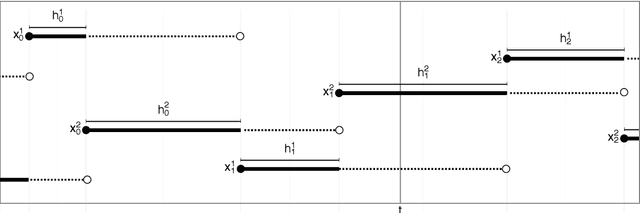
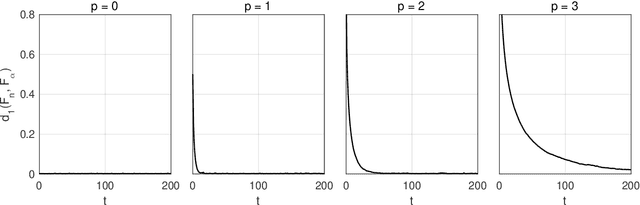
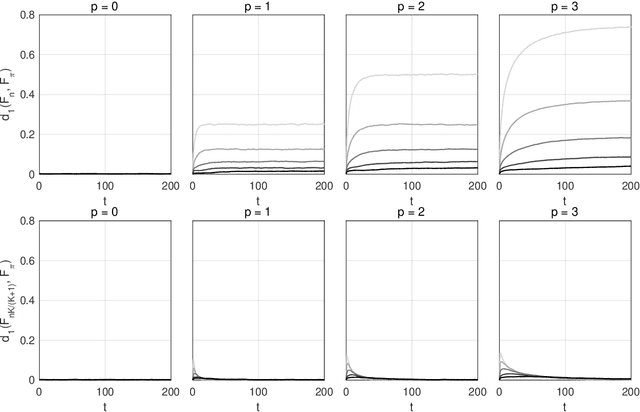
A Monte Carlo algorithm typically simulates some prescribed number of samples, taking some random real time to complete the computations necessary. This work considers the converse: to impose a real-time budget on the computation, so that the number of samples simulated is random. To complicate matters, the real time taken for each simulation may depend on the sample produced, so that the samples themselves are not independent of their number, and a length bias with respect to compute time is apparent. This is especially problematic when a Markov chain Monte Carlo (MCMC) algorithm is used and the final state of the Markov chain---rather than an average over all states---is required. The length bias does not diminish with the compute budget in this case. It occurs, for example, in sequential Monte Carlo (SMC) algorithms. We propose an anytime framework to address the concern, using a continuous-time Markov jump process to study the progress of the computation in real time. We show that the length bias can be eliminated for any MCMC algorithm by using a multiple chain construction. The utility of this construction is demonstrated on a large-scale SMC-squared implementation, using four billion particles distributed across a cluster of 128 graphics processing units on the Amazon EC2 service. The anytime framework imposes a real-time budget on the MCMC move steps within SMC-squared, ensuring that all processors are simultaneously ready for the resampling step, demonstrably reducing wait times and providing substantial control over the total compute budget.