Volume-Independent Music Matching by Frequency Spectrum Comparison

Often, I hear a piece of music and wonder what the name of the piece is. Indeed, there are applications such as Shazam app that provides music matching. However, the limitations of those apps are that the same piece performed by the same musician cannot be identified if it is not the same recording. Shazam identifies the recording of it, not the music. This is because Shazam matches the variation in volume, not the frequencies of the sound. This research attempts to match music the way humans understand it: by the frequency spectrum of music, not the volume variation. Essentially, the idea is to precompute the frequency spectrums of all the music in the database, then take the unknown piece and try to match its frequency spectrum against every segment of every music in the database. I did it by matching the frequency spectrum of the unknown piece to our database by sliding the window by 0.1 seconds and calculating the error by taking Absolute value, normalizing the audio, subtracting the normalized arrays, and taking the sum of absolute differences. The segment that shows the least error is considered the candidate for the match. The matching performance proved to be dependent on the complexity of the music. Matching simple music, such as single note pieces, was successful. However, more complex pieces, such as Chopins Ballade 4, were not successful, that is, the algorithm could not produce low error values in any of the music in the database. I suspect that it has to do with having too many notes: mismatches in the higher harmonics added up to a significant amount of errors, which swamps the calculations.

Comparison of Markov chains via weak Poincaré inequalities with application to pseudo-marginal MCMC

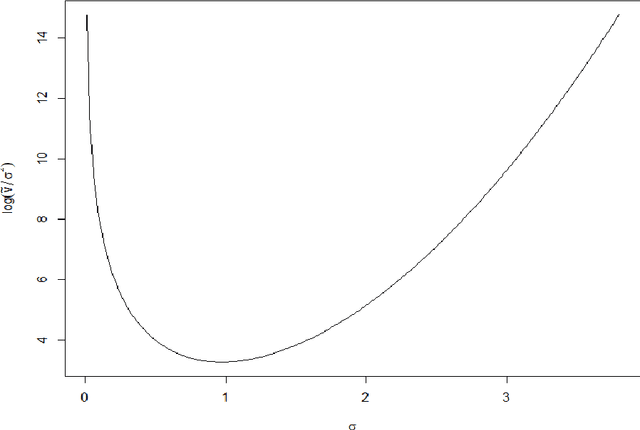
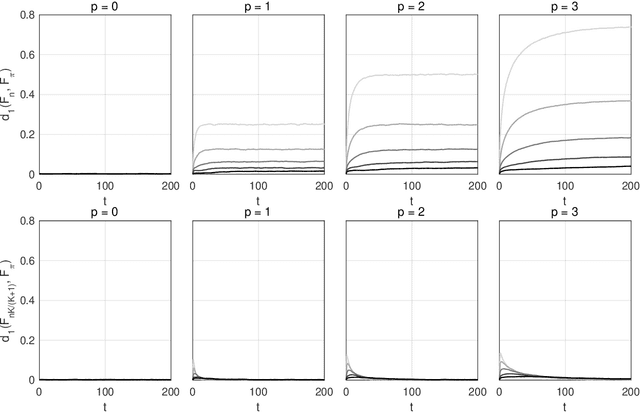
We investigate the use of a certain class of functional inequalities known as weak Poincar\'e inequalities to bound convergence of Markov chains to equilibrium. We show that this enables the straightforward and transparent derivation of subgeometric convergence bounds for methods such as the Independent Metropolis--Hastings sampler and pseudo-marginal methods for intractable likelihoods, the latter being subgeometric in many practical settings. These results rely on novel quantitative comparison theorems between Markov chains. Associated proofs are simpler than those relying on drift/minorization conditions and the tools developed allow us to recover and further extend known results as particular cases. We are then able to provide new insights into the practical use of pseudo-marginal algorithms, analyse the effect of averaging in Approximate Bayesian Computation (ABC) and the use of products of independent averages, and also to study the case of lognormal weights relevant to particle marginal Metropolis--Hastings (PMMH).

Anytime Monte Carlo

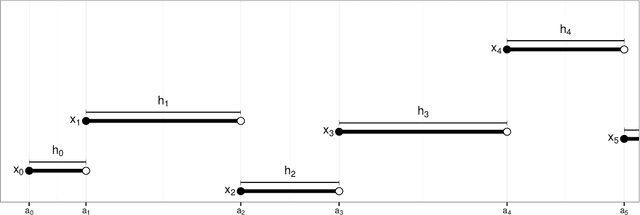
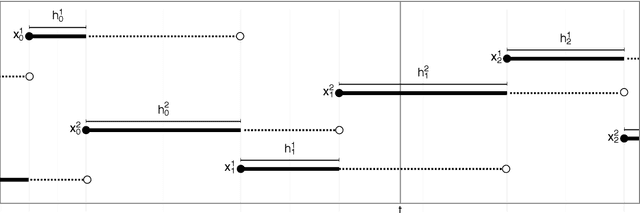
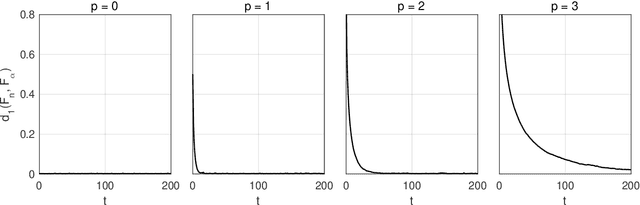
A Monte Carlo algorithm typically simulates some prescribed number of samples, taking some random real time to complete the computations necessary. This work considers the converse: to impose a real-time budget on the computation, so that the number of samples simulated is random. To complicate matters, the real time taken for each simulation may depend on the sample produced, so that the samples themselves are not independent of their number, and a length bias with respect to compute time is apparent. This is especially problematic when a Markov chain Monte Carlo (MCMC) algorithm is used and the final state of the Markov chain---rather than an average over all states---is required. The length bias does not diminish with the compute budget in this case. It occurs, for example, in sequential Monte Carlo (SMC) algorithms. We propose an anytime framework to address the concern, using a continuous-time Markov jump process to study the progress of the computation in real time. We show that the length bias can be eliminated for any MCMC algorithm by using a multiple chain construction. The utility of this construction is demonstrated on a large-scale SMC-squared implementation, using four billion particles distributed across a cluster of 128 graphics processing units on the Amazon EC2 service. The anytime framework imposes a real-time budget on the MCMC move steps within SMC-squared, ensuring that all processors are simultaneously ready for the resampling step, demonstrably reducing wait times and providing substantial control over the total compute budget.