Zack Nado
A Simple Approach to Improve Single-Model Deep Uncertainty via Distance-Awareness
May 01, 2022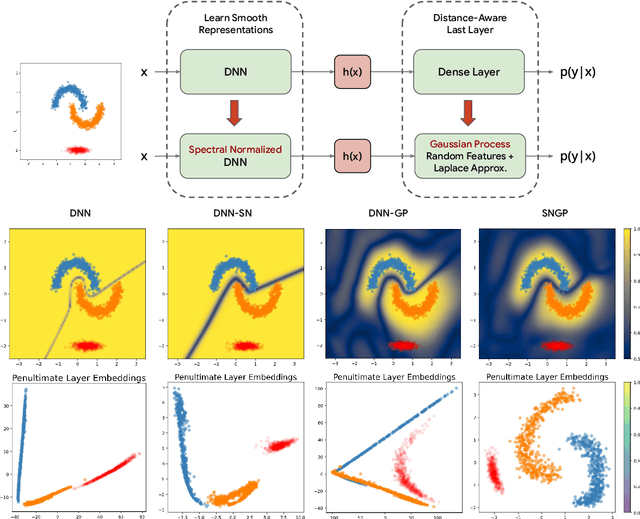
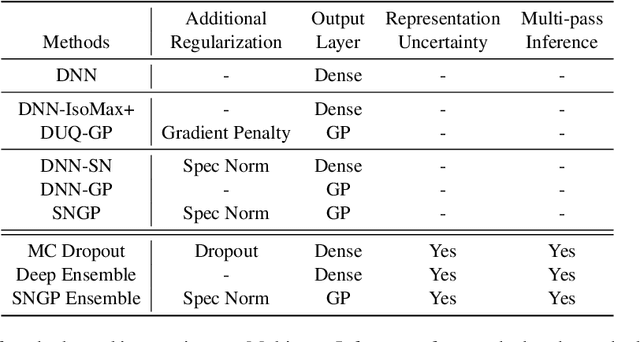
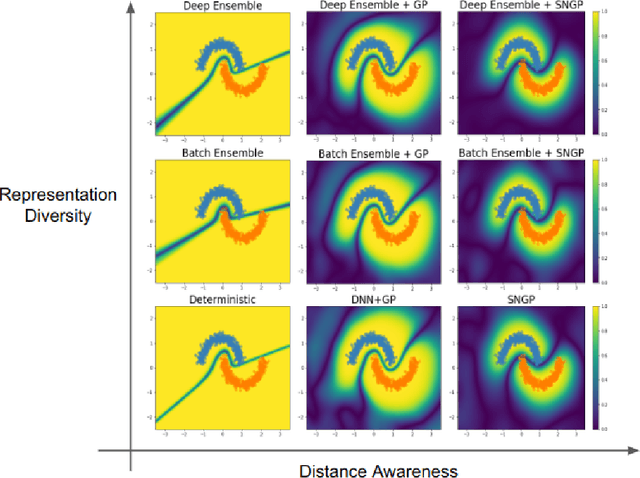
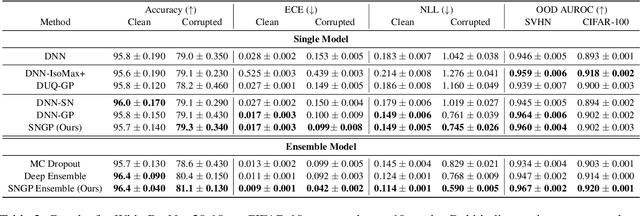
Abstract:Accurate uncertainty quantification is a major challenge in deep learning, as neural networks can make overconfident errors and assign high confidence predictions to out-of-distribution (OOD) inputs. The most popular approaches to estimate predictive uncertainty in deep learning are methods that combine predictions from multiple neural networks, such as Bayesian neural networks (BNNs) and deep ensembles. However their practicality in real-time, industrial-scale applications are limited due to the high memory and computational cost. Furthermore, ensembles and BNNs do not necessarily fix all the issues with the underlying member networks. In this work, we study principled approaches to improve uncertainty property of a single network, based on a single, deterministic representation. By formalizing the uncertainty quantification as a minimax learning problem, we first identify distance awareness, i.e., the model's ability to quantify the distance of a testing example from the training data, as a necessary condition for a DNN to achieve high-quality (i.e., minimax optimal) uncertainty estimation. We then propose Spectral-normalized Neural Gaussian Process (SNGP), a simple method that improves the distance-awareness ability of modern DNNs with two simple changes: (1) applying spectral normalization to hidden weights to enforce bi-Lipschitz smoothness in representations and (2) replacing the last output layer with a Gaussian process layer. On a suite of vision and language understanding benchmarks, SNGP outperforms other single-model approaches in prediction, calibration and out-of-domain detection. Furthermore, SNGP provides complementary benefits to popular techniques such as deep ensembles and data augmentation, making it a simple and scalable building block for probabilistic deep learning. Code is open-sourced at https://github.com/google/uncertainty-baselines
Automatic prior selection for meta Bayesian optimization with a case study on tuning deep neural network optimizers
Sep 16, 2021



Abstract:The performance of deep neural networks can be highly sensitive to the choice of a variety of meta-parameters, such as optimizer parameters and model hyperparameters. Tuning these well, however, often requires extensive and costly experimentation. Bayesian optimization (BO) is a principled approach to solve such expensive hyperparameter tuning problems efficiently. Key to the performance of BO is specifying and refining a distribution over functions, which is used to reason about the optima of the underlying function being optimized. In this work, we consider the scenario where we have data from similar functions that allows us to specify a tighter distribution a priori. Specifically, we focus on the common but potentially costly task of tuning optimizer parameters for training neural networks. Building on the meta BO method from Wang et al. (2018), we develop practical improvements that (a) boost its performance by leveraging tuning results on multiple tasks without requiring observations for the same meta-parameter points across all tasks, and (b) retain its regret bound for a special case of our method. As a result, we provide a coherent BO solution for iterative optimization of continuous optimizer parameters. To verify our approach in realistic model training setups, we collected a large multi-task hyperparameter tuning dataset by training tens of thousands of configurations of near-state-of-the-art models on popular image and text datasets, as well as a protein sequence dataset. Our results show that on average, our method is able to locate good hyperparameters at least 3 times more efficiently than the best competing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge