Towards a Unified Framework for Uncertainty-aware Nonlinear Variable Selection with Theoretical Guarantees

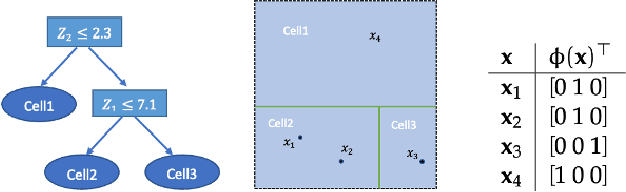
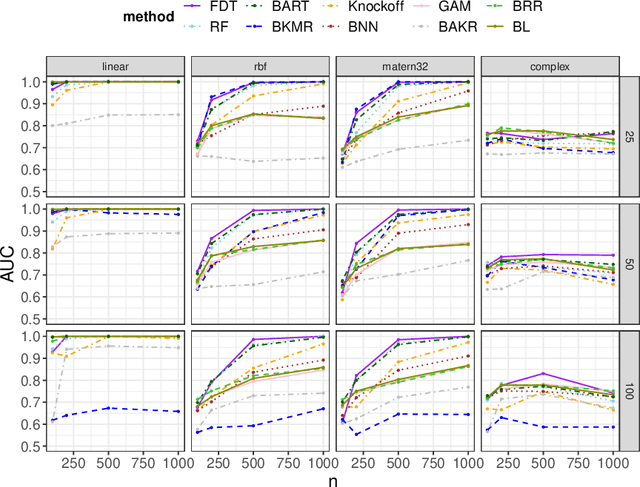
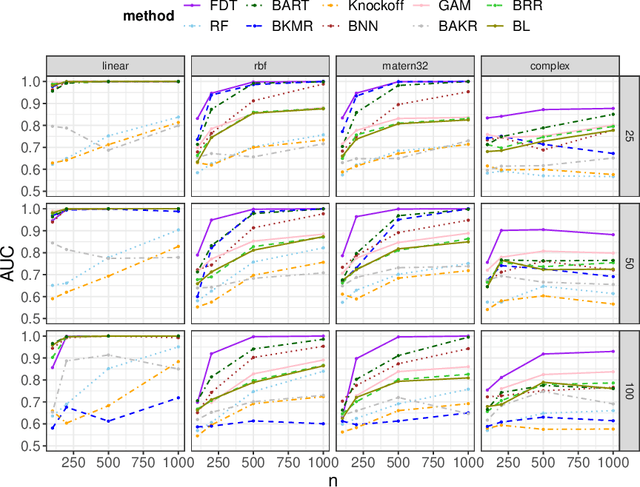
We develop a simple and unified framework for nonlinear variable selection that incorporates model uncertainty and is compatible with a wide range of machine learning models (e.g., tree ensembles, kernel methods and neural network). In particular, for a learned nonlinear model $f(\mathbf{x})$, we consider quantifying the importance of an input variable $\mathbf{x}^j$ using the integrated gradient measure $\psi_j = \Vert \frac{\partial}{\partial \mathbf{x}^j} f(\mathbf{x})\Vert^2_2$. We then (1) provide a principled approach for quantifying variable selection uncertainty by deriving its posterior distribution, and (2) show that the approach is generalizable even to non-differentiable models such as tree ensembles. Rigorous Bayesian nonparametric theorems are derived to guarantee the posterior consistency and asymptotic uncertainty of the proposed approach. Extensive simulation confirms that the proposed algorithm outperforms existing classic and recent variable selection methods.

Adaptive and Calibrated Ensemble Learning with Dependent Tail-free Process

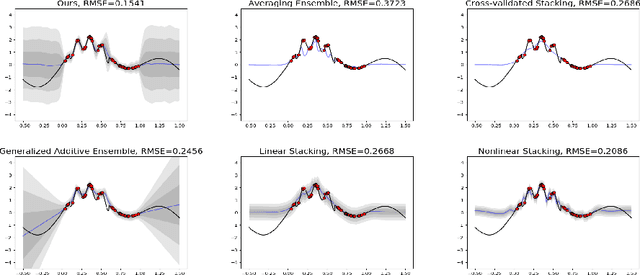
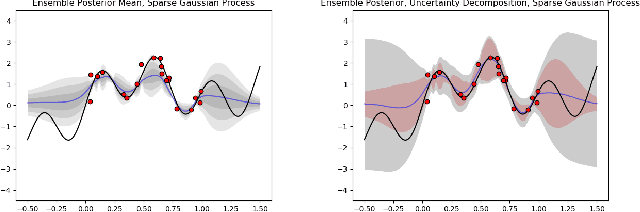
Ensemble learning is a mainstay in modern data science practice. Conventional ensemble algorithms assigns to base models a set of deterministic, constant model weights that (1) do not fully account for variations in base model accuracy across subgroups, nor (2) provide uncertainty estimates for the ensemble prediction, which could result in mis-calibrated (i.e. precise but biased) predictions that could in turn negatively impact the algorithm performance in real-word applications. In this work, we present an adaptive, probabilistic approach to ensemble learning using dependent tail-free process as ensemble weight prior. Given input feature $\mathbf{x}$, our method optimally combines base models based on their predictive accuracy in the feature space $\mathbf{x} \in \mathcal{X}$, and provides interpretable uncertainty estimates both in model selection and in ensemble prediction. To encourage scalable and calibrated inference, we derive a structured variational inference algorithm that jointly minimize KL objective and the model's calibration score (i.e. Continuous Ranked Probability Score (CRPS)). We illustrate the utility of our method on both a synthetic nonlinear function regression task, and on the real-world application of spatio-temporal integration of particle pollution prediction models in New England.