Adaptive and Calibrated Ensemble Learning with Dependent Tail-free Process
Paper and Code
Dec 19, 2018
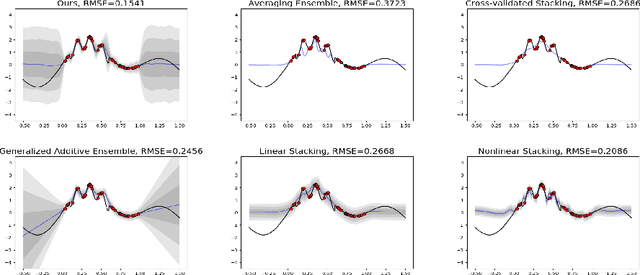

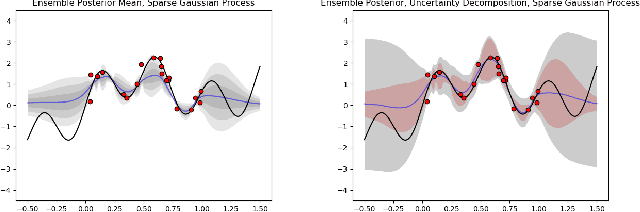
Ensemble learning is a mainstay in modern data science practice. Conventional ensemble algorithms assigns to base models a set of deterministic, constant model weights that (1) do not fully account for variations in base model accuracy across subgroups, nor (2) provide uncertainty estimates for the ensemble prediction, which could result in mis-calibrated (i.e. precise but biased) predictions that could in turn negatively impact the algorithm performance in real-word applications. In this work, we present an adaptive, probabilistic approach to ensemble learning using dependent tail-free process as ensemble weight prior. Given input feature $\mathbf{x}$, our method optimally combines base models based on their predictive accuracy in the feature space $\mathbf{x} \in \mathcal{X}$, and provides interpretable uncertainty estimates both in model selection and in ensemble prediction. To encourage scalable and calibrated inference, we derive a structured variational inference algorithm that jointly minimize KL objective and the model's calibration score (i.e. Continuous Ranked Probability Score (CRPS)). We illustrate the utility of our method on both a synthetic nonlinear function regression task, and on the real-world application of spatio-temporal integration of particle pollution prediction models in New England.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge