Brent Coull
Accurate Uncertainty Estimation and Decomposition in Ensemble Learning
Nov 11, 2019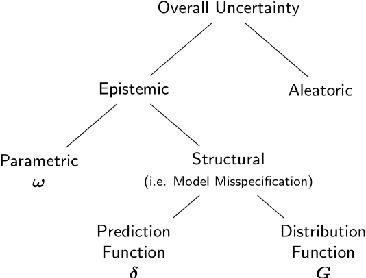
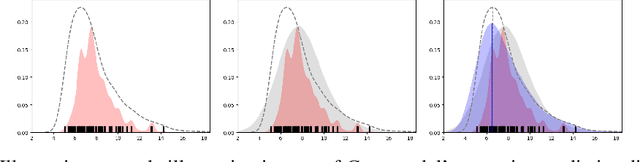
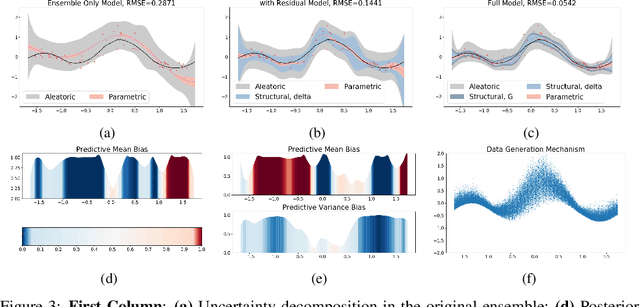
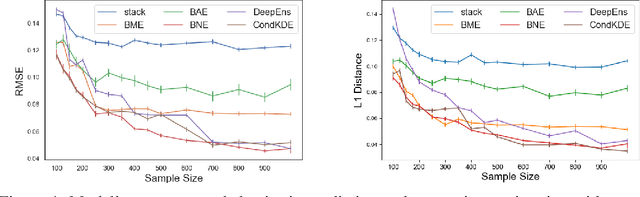
Abstract:Ensemble learning is a standard approach to building machine learning systems that capture complex phenomena in real-world data. An important aspect of these systems is the complete and valid quantification of model uncertainty. We introduce a Bayesian nonparametric ensemble (BNE) approach that augments an existing ensemble model to account for different sources of model uncertainty. BNE augments a model's prediction and distribution functions using Bayesian nonparametric machinery. It has a theoretical guarantee in that it robustly estimates the uncertainty patterns in the data distribution, and can decompose its overall predictive uncertainty into distinct components that are due to different sources of noise and error. We show that our method achieves accurate uncertainty estimates under complex observational noise, and illustrate its real-world utility in terms of uncertainty decomposition and model bias detection for an ensemble in predict air pollution exposures in Eastern Massachusetts, USA.
Robust Hypothesis Test for Nonlinear Effect with Gaussian Processes
Oct 27, 2017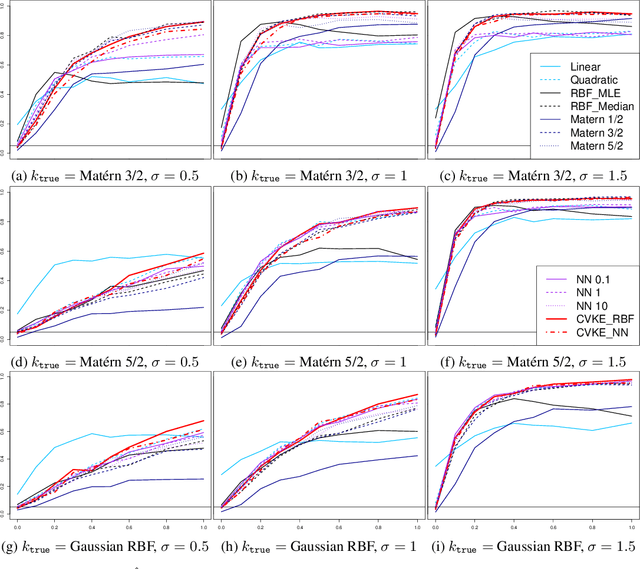
Abstract:This work constructs a hypothesis test for detecting whether an data-generating function $h: R^p \rightarrow R$ belongs to a specific reproducing kernel Hilbert space $\mathcal{H}_0$ , where the structure of $\mathcal{H}_0$ is only partially known. Utilizing the theory of reproducing kernels, we reduce this hypothesis to a simple one-sided score test for a scalar parameter, develop a testing procedure that is robust against the mis-specification of kernel functions, and also propose an ensemble-based estimator for the null model to guarantee test performance in small samples. To demonstrate the utility of the proposed method, we apply our test to the problem of detecting nonlinear interaction between groups of continuous features. We evaluate the finite-sample performance of our test under different data-generating functions and estimation strategies for the null model. Our results reveal interesting connections between notions in machine learning (model underfit/overfit) and those in statistical inference (i.e. Type I error/power of hypothesis test), and also highlight unexpected consequences of common model estimating strategies (e.g. estimating kernel hyperparameters using maximum likelihood estimation) on model inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge