Adaptive Elicitation of Latent Information Using Natural Language

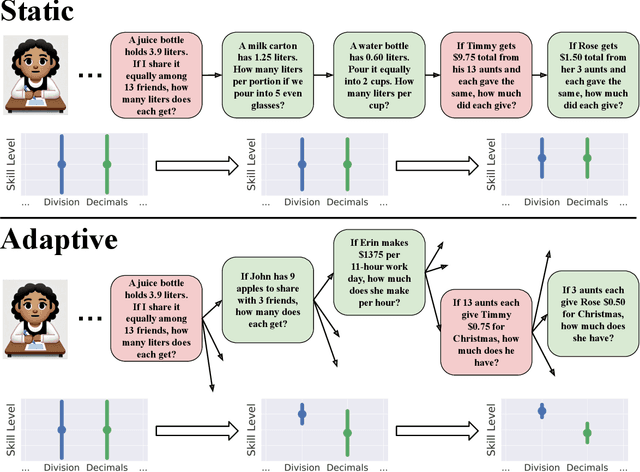
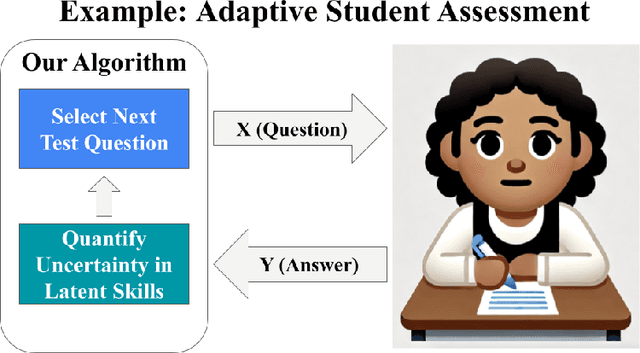
Eliciting information to reduce uncertainty about a latent entity is a critical task in many application domains, e.g., assessing individual student learning outcomes, diagnosing underlying diseases, or learning user preferences. Though natural language is a powerful medium for this purpose, large language models (LLMs) and existing fine-tuning algorithms lack mechanisms for strategically gathering information to refine their own understanding of the latent entity. To harness the generalization power and world knowledge of LLMs in developing effective information-gathering strategies, we propose an adaptive elicitation framework that actively reduces uncertainty on the latent entity. Since probabilistic modeling of an abstract latent entity is difficult, our framework adopts a predictive view of uncertainty, using a meta-learned language model to simulate future observations and enable scalable uncertainty quantification over complex natural language. Through autoregressive forward simulation, our model quantifies how new questions reduce epistemic uncertainty, enabling the development of sophisticated information-gathering strategies to choose the most informative next queries. In experiments on the 20 questions game, dynamic opinion polling, and adaptive student assessment, our method consistently outperforms baselines in identifying critical unknowns and improving downstream predictions, illustrating the promise of strategic information gathering in natural language settings.

Mathematical Programming For Adaptive Experiments

Adaptive experimentation can significantly improve statistical power, but standard algorithms overlook important practical issues including batched and delayed feedback, personalization, non-stationarity, multiple objectives, and constraints. To address these issues, the current algorithm design paradigm crafts tailored methods for each problem instance. Since it is infeasible to devise novel algorithms for every real-world instance, practitioners often have to resort to suboptimal approximations that do not address all of their challenges. Moving away from developing bespoke algorithms for each setting, we present a mathematical programming view of adaptive experimentation that can flexibly incorporate a wide range of objectives, constraints, and statistical procedures. By formulating a dynamic program in the batched limit, our modeling framework enables the use of scalable optimization methods (e.g., SGD and auto-differentiation) to solve for treatment allocations. We evaluate our framework on benchmarks modeled after practical challenges such as non-stationarity, personalization, multi-objectives, and constraints. Unlike bespoke algorithms such as modified variants of Thomson sampling, our mathematical programming approach provides remarkably robust performance across instances.

AExGym: Benchmarks and Environments for Adaptive Experimentation

Innovations across science and industry are evaluated using randomized trials (a.k.a. A/B tests). While simple and robust, such static designs are inefficient or infeasible for testing many hypotheses. Adaptive designs can greatly improve statistical power in theory, but they have seen limited adoption due to their fragility in practice. We present a benchmark for adaptive experimentation based on real-world datasets, highlighting prominent practical challenges to operationalizing adaptivity: non-stationarity, batched/delayed feedback, multiple outcomes and objectives, and external validity. Our benchmark aims to spur methodological development that puts practical performance (e.g., robustness) as a central concern, rather than mathematical guarantees on contrived instances. We release an open source library, AExGym, which is designed with modularity and extensibility in mind to allow experimentation practitioners to develop custom environments and algorithms.

TpopT: Efficient Trainable Template Optimization on Low-Dimensional Manifolds

In scientific and engineering scenarios, a recurring task is the detection of low-dimensional families of signals or patterns. A classic family of approaches, exemplified by template matching, aims to cover the search space with a dense template bank. While simple and highly interpretable, it suffers from poor computational efficiency due to unfavorable scaling in the signal space dimensionality. In this work, we study TpopT (TemPlate OPTimization) as an alternative scalable framework for detecting low-dimensional families of signals which maintains high interpretability. We provide a theoretical analysis of the convergence of Riemannian gradient descent for TpopT, and prove that it has a superior dimension scaling to covering. We also propose a practical TpopT framework for nonparametric signal sets, which incorporates techniques of embedding and kernel interpolation, and is further configurable into a trainable network architecture by unrolled optimization. The proposed trainable TpopT exhibits significantly improved efficiency-accuracy tradeoffs for gravitational wave detection, where matched filtering is currently a method of choice. We further illustrate the general applicability of this approach with experiments on handwritten digit data.