Detecting and Diagnosing Terrestrial Gravitational-Wave Mimics Through Feature Learning

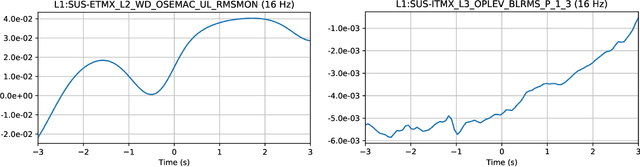
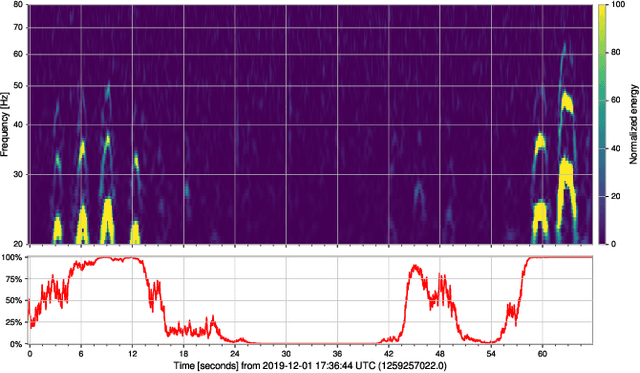
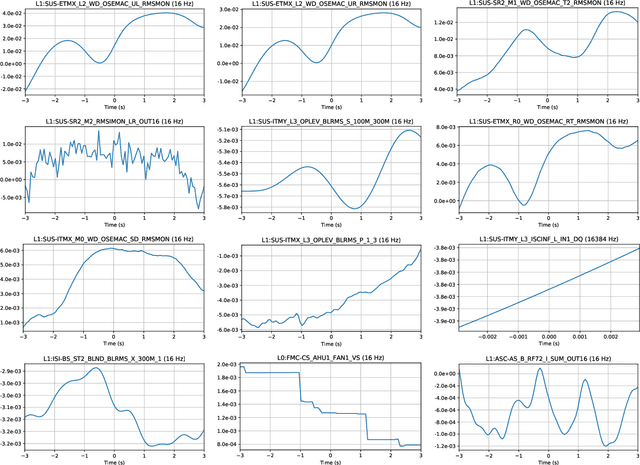
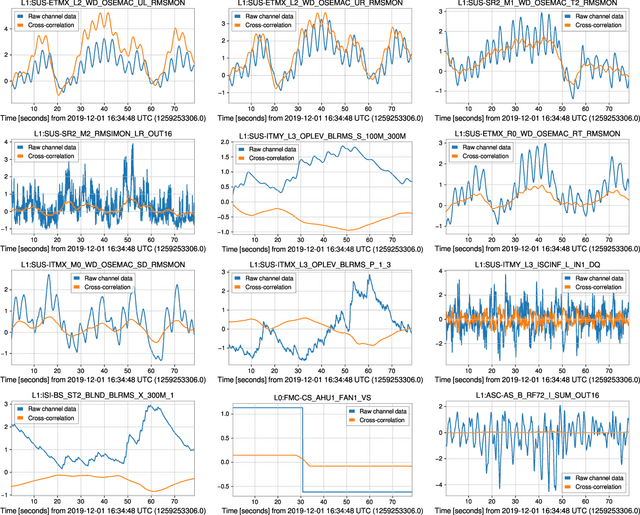
As engineered systems grow in complexity, there is an increasing need for automatic methods that can detect, diagnose, and even correct transient anomalies that inevitably arise and can be difficult or impossible to diagnose and fix manually. Among the most sensitive and complex systems of our civilization are the detectors that search for incredibly small variations in distance caused by gravitational waves -- phenomena originally predicted by Albert Einstein to emerge and propagate through the universe as the result of collisions between black holes and other massive objects in deep space. The extreme complexity and precision of such detectors causes them to be subject to transient noise issues that can significantly limit their sensitivity and effectiveness. In this work, we present a demonstration of a method that can detect and characterize emergent transient anomalies of such massively complex systems. We illustrate the performance, precision, and adaptability of the automated solution via one of the prevalent issues limiting gravitational-wave discoveries: noise artifacts of terrestrial origin that contaminate gravitational wave observatories' highly sensitive measurements and can obscure or even mimic the faint astrophysical signals for which they are listening. Specifically, we demonstrate how a highly interpretable convolutional classifier can automatically learn to detect transient anomalies from auxiliary detector data without needing to observe the anomalies themselves. We also illustrate several other useful features of the model, including how it performs automatic variable selection to reduce tens of thousands of auxiliary data channels to only a few relevant ones; how it identifies behavioral signatures predictive of anomalies in those channels; and how it can be used to investigate individual anomalies and the channels associated with them.

Architectural Optimization and Feature Learning for High-Dimensional Time Series Datasets

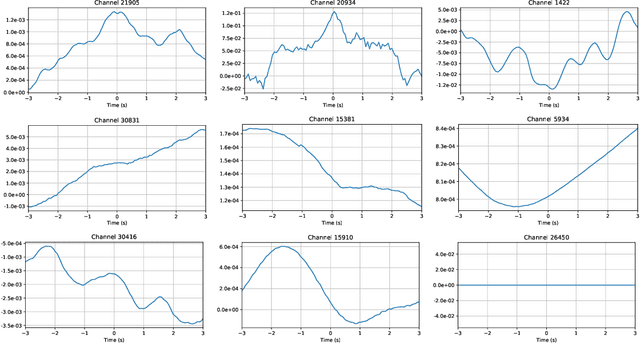
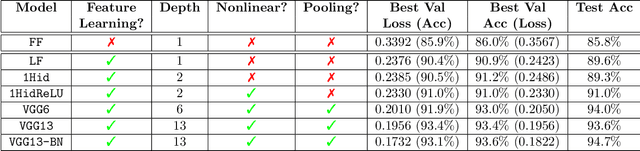
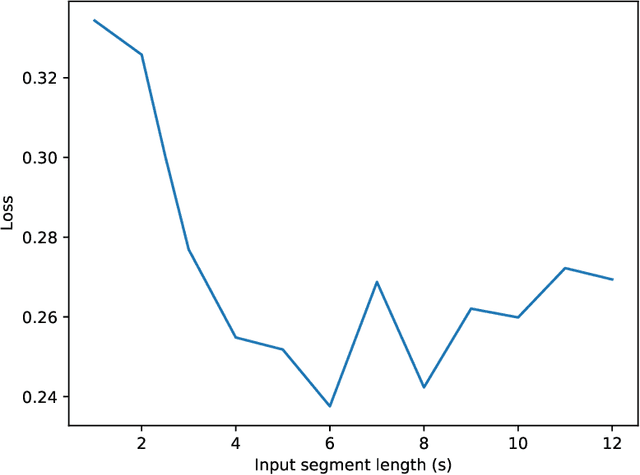
As our ability to sense increases, we are experiencing a transition from data-poor problems, in which the central issue is a lack of relevant data, to data-rich problems, in which the central issue is to identify a few relevant features in a sea of observations. Motivated by applications in gravitational-wave astrophysics, we study the problem of predicting the presence of transient noise artifacts in a gravitational wave detector from a rich collection of measurements from the detector and its environment. We argue that feature learning--in which relevant features are optimized from data--is critical to achieving high accuracy. We introduce models that reduce the error rate by over 60\% compared to the previous state of the art, which used fixed, hand-crafted features. Feature learning is useful not only because it improves performance on prediction tasks; the results provide valuable information about patterns associated with phenomena of interest that would otherwise be undiscoverable. In our application, features found to be associated with transient noise provide diagnostic information about its origin and suggest mitigation strategies. Learning in high-dimensional settings is challenging. Through experiments with a variety of architectures, we identify two key factors in successful models: sparsity, for selecting relevant variables within the high-dimensional observations; and depth, which confers flexibility for handling complex interactions and robustness with respect to temporal variations. We illustrate their significance through systematic experiments on real detector data. Our results provide experimental corroboration of common assumptions in the machine-learning community and have direct applicability to improving our ability to sense gravitational waves, as well as to many other problem settings with similarly high-dimensional, noisy, or partly irrelevant data.

Generalized Approach to Matched Filtering using Neural Networks

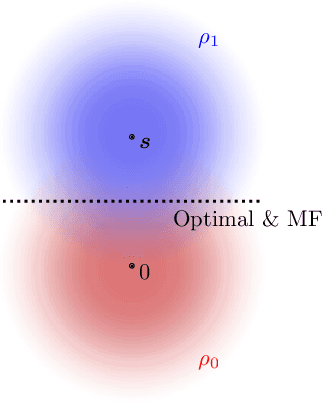
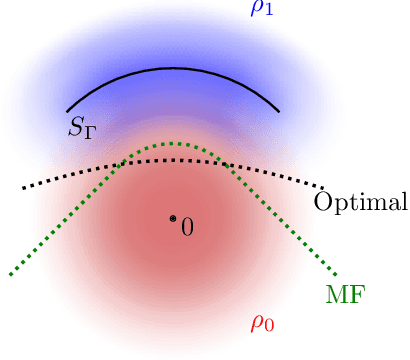
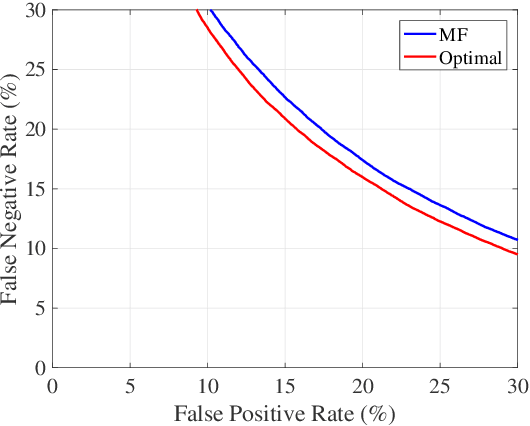
Gravitational wave science is a pioneering field with rapidly evolving data analysis methodology currently assimilating and inventing deep learning techniques. The bulk of the sophisticated flagship searches of the field rely on the time-tested matched filtering principle within their core. In this paper, we make a key observation on the relationship between the emerging deep learning and the traditional techniques: matched filtering is formally equivalent to a particular neural network. This means that a neural network can be constructed analytically to exactly implement matched filtering, and can be further trained on data or boosted with additional complexity for improved performance. This fundamental equivalence allows us to define a "complexity standard candle" allowing us to characterize the relative complexity of the different approaches to gravitational wave signals in a common framework. Additionally it also provides a glimpse of an intriguing symmetry that could provide clues on how neural networks approach the problem of finding signals in overwhelming noise. Moreover, we show that the proposed neural network architecture can outperform matched filtering, both with or without knowledge of a prior on the parameter distribution. When a prior is given, the proposed neural network can approach the statistically optimal performance. We also propose and investigate two different neural network architectures MNet-Shallow and MNet-Deep, both of which implement matched filtering at initialization and can be trained on data. MNet-Shallow has simpler structure, while MNet-Deep is more flexible and can deal with a wider range of distributions. Our theoretical findings are corroborated by experiments using real LIGO data and synthetic injections. Finally, our results suggest new perspectives on the role of deep learning in gravitational wave detection.