Fast, Accurate Manifold Denoising by Tunneling Riemannian Optimization

Learned denoisers play a fundamental role in various signal generation (e.g., diffusion models) and reconstruction (e.g., compressed sensing) architectures, whose success derives from their ability to leverage low-dimensional structure in data. Existing denoising methods, however, either rely on local approximations that require a linear scan of the entire dataset or treat denoising as generic function approximation problems, often sacrificing efficiency and interpretability. We consider the problem of efficiently denoising a new noisy data point sampled from an unknown $d$-dimensional manifold $M \in \mathbb{R}^D$, using only noisy samples. This work proposes a framework for test-time efficient manifold denoising, by framing the concept of "learning-to-denoise" as "learning-to-optimize". We have two technical innovations: (i) online learning methods which learn to optimize over the manifold of clean signals using only noisy data, effectively "growing" an optimizer one sample at a time. (ii) mixed-order methods which guarantee that the learned optimizers achieve global optimality, ensuring both efficiency and near-optimal denoising performance. We corroborate these claims with theoretical analyses of both the complexity and denoising performance of mixed-order traversal. Our experiments on scientific manifolds demonstrate significantly improved complexity-performance tradeoffs compared to nearest neighbor search, which underpins existing provable denoising approaches based on exhaustive search.

Generalized Approach to Matched Filtering using Neural Networks

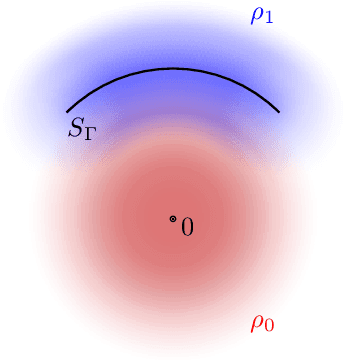
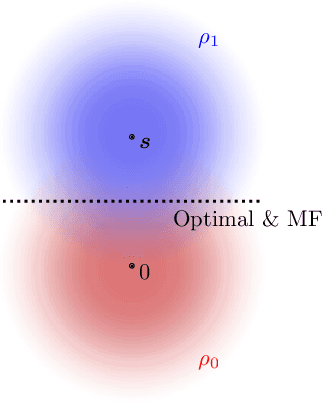
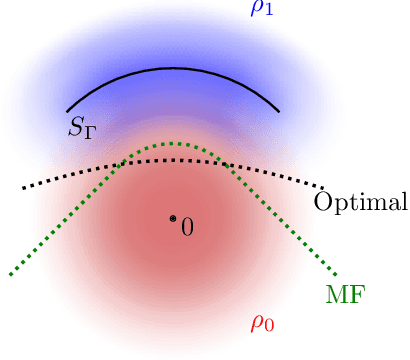
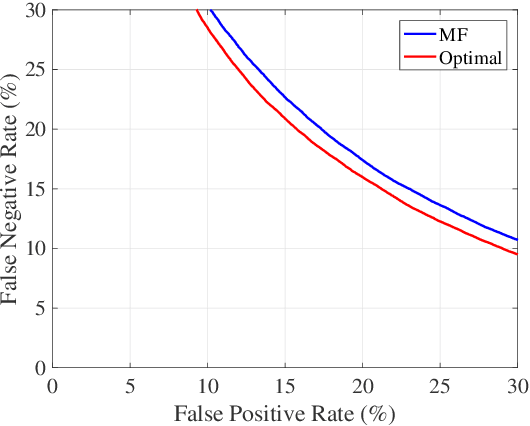
Gravitational wave science is a pioneering field with rapidly evolving data analysis methodology currently assimilating and inventing deep learning techniques. The bulk of the sophisticated flagship searches of the field rely on the time-tested matched filtering principle within their core. In this paper, we make a key observation on the relationship between the emerging deep learning and the traditional techniques: matched filtering is formally equivalent to a particular neural network. This means that a neural network can be constructed analytically to exactly implement matched filtering, and can be further trained on data or boosted with additional complexity for improved performance. This fundamental equivalence allows us to define a "complexity standard candle" allowing us to characterize the relative complexity of the different approaches to gravitational wave signals in a common framework. Additionally it also provides a glimpse of an intriguing symmetry that could provide clues on how neural networks approach the problem of finding signals in overwhelming noise. Moreover, we show that the proposed neural network architecture can outperform matched filtering, both with or without knowledge of a prior on the parameter distribution. When a prior is given, the proposed neural network can approach the statistically optimal performance. We also propose and investigate two different neural network architectures MNet-Shallow and MNet-Deep, both of which implement matched filtering at initialization and can be trained on data. MNet-Shallow has simpler structure, while MNet-Deep is more flexible and can deal with a wider range of distributions. Our theoretical findings are corroborated by experiments using real LIGO data and synthetic injections. Finally, our results suggest new perspectives on the role of deep learning in gravitational wave detection.