SFT Memorizes, RL Generalizes: A Comparative Study of Foundation Model Post-training

Supervised fine-tuning (SFT) and reinforcement learning (RL) are widely used post-training techniques for foundation models. However, their roles in enhancing model generalization capabilities remain unclear. This paper studies the difference between SFT and RL on generalization and memorization, focusing on text-based rule variants and visual variants. We introduce GeneralPoints, an arithmetic reasoning card game, and adopt V-IRL, a real-world navigation environment, to assess how models trained with SFT and RL generalize to unseen variants in both textual and visual domains. We show that RL, especially when trained with an outcome-based reward, generalizes across both rule-based textual and visual variants. SFT, in contrast, tends to memorize training data and struggles to generalize out-of-distribution scenarios. Further analysis reveals that RL improves the model's underlying visual recognition capabilities, contributing to its enhanced generalization in the visual domain. Despite RL's superior generalization, we show that SFT remains essential for effective RL training; SFT stabilizes the model's output format, enabling subsequent RL to achieve its performance gains. These findings demonstrates the capability of RL for acquiring generalizable knowledge in complex, multi-modal tasks.

White-Box Transformers via Sparse Rate Reduction: Compression Is All There Is?

In this paper, we contend that a natural objective of representation learning is to compress and transform the distribution of the data, say sets of tokens, towards a low-dimensional Gaussian mixture supported on incoherent subspaces. The goodness of such a representation can be evaluated by a principled measure, called sparse rate reduction, that simultaneously maximizes the intrinsic information gain and extrinsic sparsity of the learned representation. From this perspective, popular deep network architectures, including transformers, can be viewed as realizing iterative schemes to optimize this measure. Particularly, we derive a transformer block from alternating optimization on parts of this objective: the multi-head self-attention operator compresses the representation by implementing an approximate gradient descent step on the coding rate of the features, and the subsequent multi-layer perceptron sparsifies the features. This leads to a family of white-box transformer-like deep network architectures, named CRATE, which are mathematically fully interpretable. We show, by way of a novel connection between denoising and compression, that the inverse to the aforementioned compressive encoding can be realized by the same class of CRATE architectures. Thus, the so-derived white-box architectures are universal to both encoders and decoders. Experiments show that these networks, despite their simplicity, indeed learn to compress and sparsify representations of large-scale real-world image and text datasets, and achieve performance very close to highly engineered transformer-based models: ViT, MAE, DINO, BERT, and GPT2. We believe the proposed computational framework demonstrates great potential in bridging the gap between theory and practice of deep learning, from a unified perspective of data compression. Code is available at: https://ma-lab-berkeley.github.io/CRATE .

Emergence of Segmentation with Minimalistic White-Box Transformers

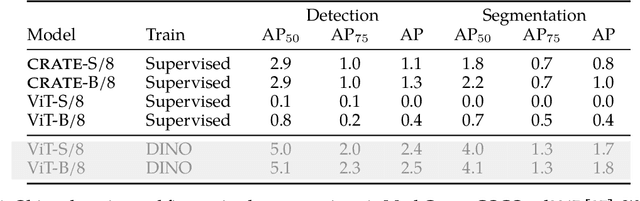
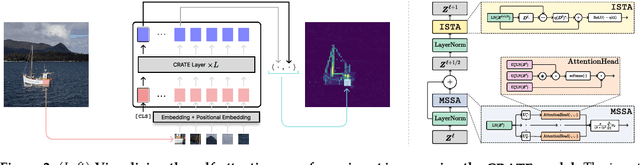
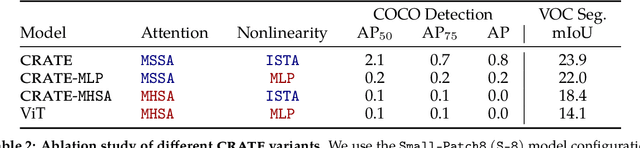
Transformer-like models for vision tasks have recently proven effective for a wide range of downstream applications such as segmentation and detection. Previous works have shown that segmentation properties emerge in vision transformers (ViTs) trained using self-supervised methods such as DINO, but not in those trained on supervised classification tasks. In this study, we probe whether segmentation emerges in transformer-based models solely as a result of intricate self-supervised learning mechanisms, or if the same emergence can be achieved under much broader conditions through proper design of the model architecture. Through extensive experimental results, we demonstrate that when employing a white-box transformer-like architecture known as CRATE, whose design explicitly models and pursues low-dimensional structures in the data distribution, segmentation properties, at both the whole and parts levels, already emerge with a minimalistic supervised training recipe. Layer-wise finer-grained analysis reveals that the emergent properties strongly corroborate the designed mathematical functions of the white-box network. Our results suggest a path to design white-box foundation models that are simultaneously highly performant and mathematically fully interpretable. Code is at \url{https://github.com/Ma-Lab-Berkeley/CRATE}.

Image Clustering via the Principle of Rate Reduction in the Age of Pretrained Models

The advent of large pre-trained models has brought about a paradigm shift in both visual representation learning and natural language processing. However, clustering unlabeled images, as a fundamental and classic machine learning problem, still lacks effective solution, particularly for large-scale datasets. In this paper, we propose a novel image clustering pipeline that leverages the powerful feature representation of large pre-trained models such as CLIP and cluster images effectively and efficiently at scale. We show that the pre-trained features are significantly more structured by further optimizing the rate reduction objective. The resulting features may significantly improve the clustering accuracy, e.g., from 57\% to 66\% on ImageNet-1k. Furthermore, by leveraging CLIP's image-text binding, we show how the new clustering method leads to a simple yet effective self-labeling algorithm that successfully works on unlabeled large datasets such as MS-COCO and LAION-Aesthetics. We will release the code in https://github.com/LeslieTrue/CPP.

White-Box Transformers via Sparse Rate Reduction

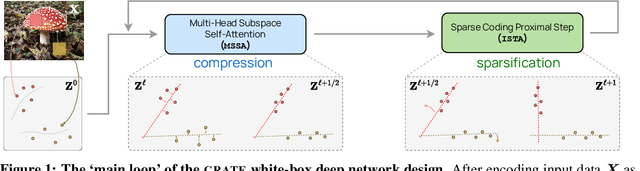
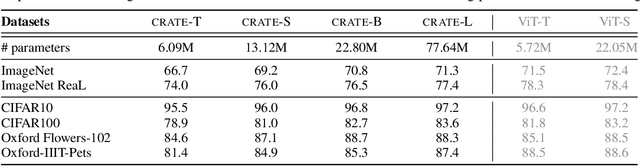
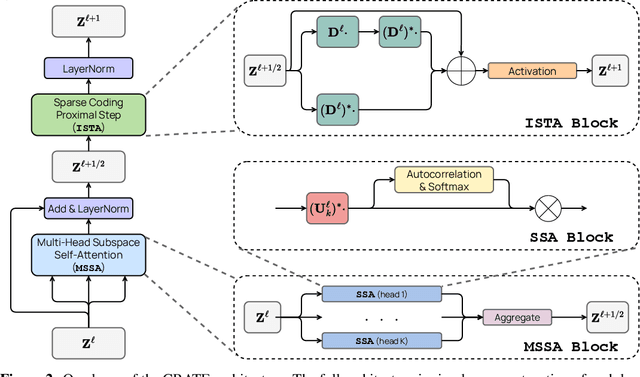
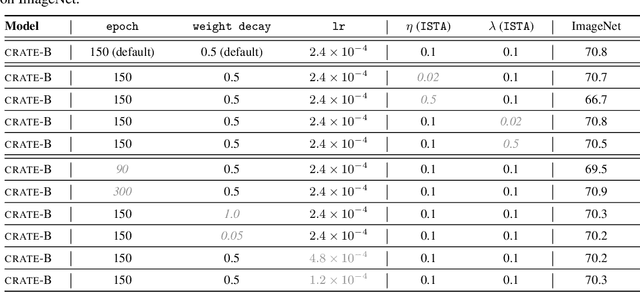
In this paper, we contend that the objective of representation learning is to compress and transform the distribution of the data, say sets of tokens, towards a mixture of low-dimensional Gaussian distributions supported on incoherent subspaces. The quality of the final representation can be measured by a unified objective function called sparse rate reduction. From this perspective, popular deep networks such as transformers can be naturally viewed as realizing iterative schemes to optimize this objective incrementally. Particularly, we show that the standard transformer block can be derived from alternating optimization on complementary parts of this objective: the multi-head self-attention operator can be viewed as a gradient descent step to compress the token sets by minimizing their lossy coding rate, and the subsequent multi-layer perceptron can be viewed as attempting to sparsify the representation of the tokens. This leads to a family of white-box transformer-like deep network architectures which are mathematically fully interpretable. Despite their simplicity, experiments show that these networks indeed learn to optimize the designed objective: they compress and sparsify representations of large-scale real-world vision datasets such as ImageNet, and achieve performance very close to thoroughly engineered transformers such as ViT. Code is at \url{https://github.com/Ma-Lab-Berkeley/CRATE}.