Learned Finite Element-based Regularization of the Inverse Problem in Electrocardiographic Imaging

Electrocardiographic imaging (ECGI) seeks to reconstruct cardiac electrical activity from body-surface potentials noninvasively. However, the associated inverse problem is severely ill-posed and requires robust regularization. While classical approaches primarily employ spatial smoothing, the temporal structure of cardiac dynamics remains underexploited despite its physiological relevance. We introduce a space-time regularization framework that couples spatial regularization with a learned temporal Fields-of-Experts (FoE) prior to capture complex spatiotemporal activation patterns. We derive a finite element discretization on unstructured cardiac surface meshes, prove Mosco-convergence, and develop a scalable optimization algorithm capable of handling the FoE term. Numerical experiments on synthetic epicardial data demonstrate improved denoising and inverse reconstructions compared to handcrafted spatiotemporal methods, yielding solutions that are both robust to noise and physiologically plausible.

Stochastic Siamese MAE Pretraining for Longitudinal Medical Images

Temporally aware image representations are crucial for capturing disease progression in 3D volumes of longitudinal medical datasets. However, recent state-of-the-art self-supervised learning approaches like Masked Autoencoding (MAE), despite their strong representation learning capabilities, lack temporal awareness. In this paper, we propose STAMP (Stochastic Temporal Autoencoder with Masked Pretraining), a Siamese MAE framework that encodes temporal information through a stochastic process by conditioning on the time difference between the 2 input volumes. Unlike deterministic Siamese approaches, which compare scans from different time points but fail to account for the inherent uncertainty in disease evolution, STAMP learns temporal dynamics stochastically by reframing the MAE reconstruction loss as a conditional variational inference objective. We evaluated STAMP on two OCT and one MRI datasets with multiple visits per patient. STAMP pretrained ViT models outperformed both existing temporal MAE methods and foundation models on different late stage Age-Related Macular Degeneration and Alzheimer's Disease progression prediction which require models to learn the underlying non-deterministic temporal dynamics of the diseases.

Efficient MedSAMs: Segment Anything in Medical Images on Laptop

Promptable segmentation foundation models have emerged as a transformative approach to addressing the diverse needs in medical images, but most existing models require expensive computing, posing a big barrier to their adoption in clinical practice. In this work, we organized the first international competition dedicated to promptable medical image segmentation, featuring a large-scale dataset spanning nine common imaging modalities from over 20 different institutions. The top teams developed lightweight segmentation foundation models and implemented an efficient inference pipeline that substantially reduced computational requirements while maintaining state-of-the-art segmentation accuracy. Moreover, the post-challenge phase advanced the algorithms through the design of performance booster and reproducibility tasks, resulting in improved algorithms and validated reproducibility of the winning solution. Furthermore, the best-performing algorithms have been incorporated into the open-source software with a user-friendly interface to facilitate clinical adoption. The data and code are publicly available to foster the further development of medical image segmentation foundation models and pave the way for impactful real-world applications.

Finite element-based space-time total variation-type regularization of the inverse problem in electrocardiographic imaging

Reconstructing cardiac electrical activity from body surface electric potential measurements results in the severely ill-posed inverse problem in electrocardiography. Many different regularization approaches have been proposed to improve numerical results and provide unique results. This work presents a novel approach for reconstructing the epicardial potential from body surface potential maps based on a space-time total variation-type regularization using finite elements, where a first-order primal-dual algorithm solves the underlying convex optimization problem. In several numerical experiments, the superior performance of this method and the benefit of space-time regularization for the reconstruction of epicardial potential on two-dimensional torso data and a three-dimensional rabbit heart compared to state-of-the-art methods are demonstrated.

Gadolinium dose reduction for brain MRI using conditional deep learning

Recently, deep learning (DL)-based methods have been proposed for the computational reduction of gadolinium-based contrast agents (GBCAs) to mitigate adverse side effects while preserving diagnostic value. Currently, the two main challenges for these approaches are the accurate prediction of contrast enhancement and the synthesis of realistic images. In this work, we address both challenges by utilizing the contrast signal encoded in the subtraction images of pre-contrast and post-contrast image pairs. To avoid the synthesis of any noise or artifacts and solely focus on contrast signal extraction and enhancement from low-dose subtraction images, we train our DL model using noise-free standard-dose subtraction images as targets. As a result, our model predicts the contrast enhancement signal only; thereby enabling synthesization of images beyond the standard dose. Furthermore, we adapt the embedding idea of recent diffusion-based models to condition our model on physical parameters affecting the contrast enhancement behavior. We demonstrate the effectiveness of our approach on synthetic and real datasets using various scanners, field strengths, and contrast agents.

Faithful Synthesis of Low-dose Contrast-enhanced Brain MRI Scans using Noise-preserving Conditional GANs

Today Gadolinium-based contrast agents (GBCA) are indispensable in Magnetic Resonance Imaging (MRI) for diagnosing various diseases. However, GBCAs are expensive and may accumulate in patients with potential side effects, thus dose-reduction is recommended. Still, it is unclear to which extent the GBCA dose can be reduced while preserving the diagnostic value -- especially in pathological regions. To address this issue, we collected brain MRI scans at numerous non-standard GBCA dosages and developed a conditional GAN model for synthesizing corresponding images at fractional dose levels. Along with the adversarial loss, we advocate a novel content loss function based on the Wasserstein distance of locally paired patch statistics for the faithful preservation of noise. Our numerical experiments show that conditional GANs are suitable for generating images at different GBCA dose levels and can be used to augment datasets for virtual contrast models. Moreover, our model can be transferred to openly available datasets such as BraTS, where non-standard GBCA dosage images do not exist.

Shared Prior Learning of Energy-Based Models for Image Reconstruction

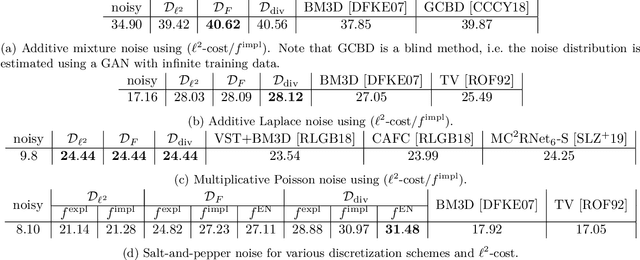
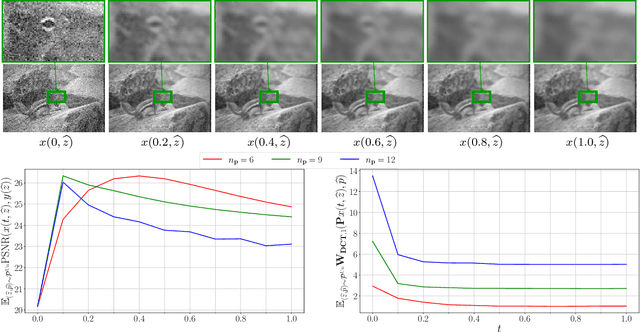
We propose a novel learning-based framework for image reconstruction particularly designed for training without ground truth data, which has three major building blocks: energy-based learning, a patch-based Wasserstein loss functional, and shared prior learning. In energy-based learning, the parameters of an energy functional composed of a learned data fidelity term and a data-driven regularizer are computed in a mean-field optimal control problem. In the absence of ground truth data, we change the loss functional to a patch-based Wasserstein functional, in which local statistics of the output images are compared to uncorrupted reference patches. Finally, in shared prior learning, both aforementioned optimal control problems are optimized simultaneously with shared learned parameters of the regularizer to further enhance unsupervised image reconstruction. We derive several time discretization schemes of the gradient flow and verify their consistency in terms of Mosco convergence. In numerous numerical experiments, we demonstrate that the proposed method generates state-of-the-art results for various image reconstruction applications--even if no ground truth images are available for training.

On the estimation of the Wasserstein distance in generative models

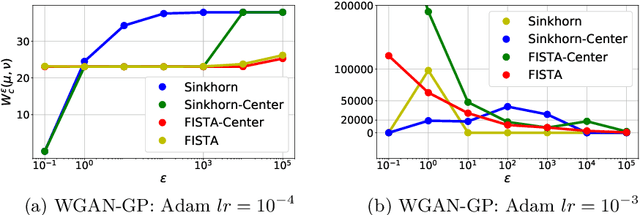
Generative Adversarial Networks (GANs) have been used to model the underlying probability distribution of sample based datasets. GANs are notoriuos for training difficulties and their dependence on arbitrary hyperparameters. One recent improvement in GAN literature is to use the Wasserstein distance as loss function leading to Wasserstein Generative Adversarial Networks (WGANs). Using this as a basis, we show various ways in which the Wasserstein distance is estimated for the task of generative modelling. Additionally, the secrets in training such models are shown and summarized at the end of this work. Where applicable, we extend current works to different algorithms, different cost functions, and different regularization schemes to improve generative models.