On the estimation of the Wasserstein distance in generative models
Paper and Code
Oct 02, 2019

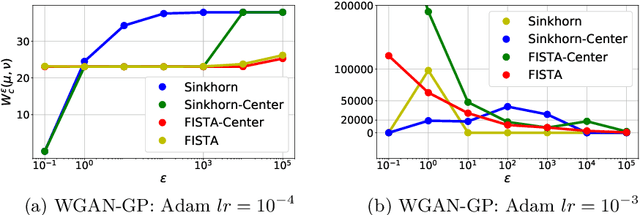

Generative Adversarial Networks (GANs) have been used to model the underlying probability distribution of sample based datasets. GANs are notoriuos for training difficulties and their dependence on arbitrary hyperparameters. One recent improvement in GAN literature is to use the Wasserstein distance as loss function leading to Wasserstein Generative Adversarial Networks (WGANs). Using this as a basis, we show various ways in which the Wasserstein distance is estimated for the task of generative modelling. Additionally, the secrets in training such models are shown and summarized at the end of this work. Where applicable, we extend current works to different algorithms, different cost functions, and different regularization schemes to improve generative models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge