Finite element-based space-time total variation-type regularization of the inverse problem in electrocardiographic imaging

Reconstructing cardiac electrical activity from body surface electric potential measurements results in the severely ill-posed inverse problem in electrocardiography. Many different regularization approaches have been proposed to improve numerical results and provide unique results. This work presents a novel approach for reconstructing the epicardial potential from body surface potential maps based on a space-time total variation-type regularization using finite elements, where a first-order primal-dual algorithm solves the underlying convex optimization problem. In several numerical experiments, the superior performance of this method and the benefit of space-time regularization for the reconstruction of epicardial potential on two-dimensional torso data and a three-dimensional rabbit heart compared to state-of-the-art methods are demonstrated.

Shape of my heart: Cardiac models through learned signed distance functions

The efficient construction of an anatomical model is one of the major challenges of patient-specific in-silico models of the human heart. Current methods frequently rely on linear statistical models, allowing no advanced topological changes, or requiring medical image segmentation followed by a meshing pipeline, which strongly depends on image resolution, quality, and modality. These approaches are therefore limited in their transferability to other imaging domains. In this work, the cardiac shape is reconstructed by means of three-dimensional deep signed distance functions with Lipschitz regularity. For this purpose, the shapes of cardiac MRI reconstructions are learned from public databases to model the spatial relation of multiple chambers in Cartesian space. We demonstrate that this approach is also capable of reconstructing anatomical models from partial data, such as point clouds from a single ventricle, or modalities different from the trained MRI, such as electroanatomical mapping, and in addition, allows us to generate new anatomical shapes by randomly sampling latent vectors.

Digital twinning of cardiac electrophysiology models from the surface ECG: a geodesic backpropagation approach

The eikonal equation has become an indispensable tool for modeling cardiac electrical activation accurately and efficiently. In principle, by matching clinically recorded and eikonal-based electrocardiograms (ECGs), it is possible to build patient-specific models of cardiac electrophysiology in a purely non-invasive manner. Nonetheless, the fitting procedure remains a challenging task. The present study introduces a novel method, Geodesic-BP, to solve the inverse eikonal problem. Geodesic-BP is well-suited for GPU-accelerated machine learning frameworks, allowing us to optimize the parameters of the eikonal equation to reproduce a given ECG. We show that Geodesic-BP can reconstruct a simulated cardiac activation with high accuracy in a synthetic test case, even in the presence of modeling inaccuracies. Furthermore, we apply our algorithm to a publicly available dataset of a rabbit model, with very positive results. Given the future shift towards personalized medicine, Geodesic-BP has the potential to help in future functionalizations of cardiac models meeting clinical time constraints while maintaining the physiological accuracy of state-of-the-art cardiac models.

Physics-informed neural networks to learn cardiac fiber orientation from multiple electroanatomical maps

We propose FiberNet, a method to estimate in-vivo the cardiac fiber architecture of the human atria from multiple catheter recordings of the electrical activation. Cardiac fibers play a central rolein the electro-mechanical function of the heart, yet they aredifficult to determine in-vivo, and hence rarely truly patient-specificin existing cardiac models.FiberNet learns the fibers arrangement by solvingan inverse problem with physics-informed neural networks. The inverse problem amounts to identifyingthe conduction velocity tensor of a cardiac propagation modelfrom a set of sparse activation maps. The use of multiple mapsenables the simultaneous identification of all the componentsof the conduction velocity tensor, including the local fiber angle.We extensively test FiberNet on synthetic 2-D and 3-D examples, diffusion tensor fibers, and a patient-specific case. We show that 3 maps are sufficient to accurately capture the fibers, also in thepresence of noise. With fewer maps, the role of regularization becomesprominent. Moreover, we show that the fitted model can robustlyreproduce unseen activation maps. We envision that FiberNet will help the creation of patient-specific models for personalized medicine.The full code is available at http://github.com/fsahli/FiberNet.

Smoothness and continuity of cost functionals for ECG mismatch computation

The field of cardiac electrophysiology tries to abstract, describe and finally model the electrical characteristics of a heartbeat. With recent advances in cardiac electrophysiology, models have become more powerful and descriptive as ever. However, to advance to the field of inverse electrophysiological modeling, i.e. creating models from electrical measurements such as the ECG, the less investigated field of smoothness of the simulated ECGs w.r.t. model parameters need to be further explored. The present paper discusses smoothness in terms of the whole pipeline which describes how from physiological parameters, we arrive at the simulated ECG. Employing such a pipeline, we create a test-bench of a simplified idealized left ventricle model and demonstrate the most important factors for efficient inverse modeling through smooth cost functionals. Such knowledge will be important for designing and creating inverse models in future optimization and machine learning methods.

Learning atrial fiber orientations and conductivity tensors from intracardiac maps using physics-informed neural networks

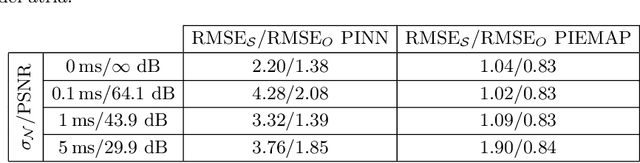
Electroanatomical maps are a key tool in the diagnosis and treatment of atrial fibrillation. Current approaches focus on the activation times recorded. However, more information can be extracted from the available data. The fibers in cardiac tissue conduct the electrical wave faster, and their direction could be inferred from activation times. In this work, we employ a recently developed approach, called physics informed neural networks, to learn the fiber orientations from electroanatomical maps, taking into account the physics of the electrical wave propagation. In particular, we train the neural network to weakly satisfy the anisotropic eikonal equation and to predict the measured activation times. We use a local basis for the anisotropic conductivity tensor, which encodes the fiber orientation. The methodology is tested both in a synthetic example and for patient data. Our approach shows good agreement in both cases and it outperforms a state of the art method in the patient data. The results show a first step towards learning the fiber orientations from electroanatomical maps with physics-informed neural networks.