Gundolf Haase
Non-Intrusive Parametrized-Background Data-Weak Reconstruction of Cardiac Displacement Fields from Sparse MRI-like Observations
Sep 18, 2025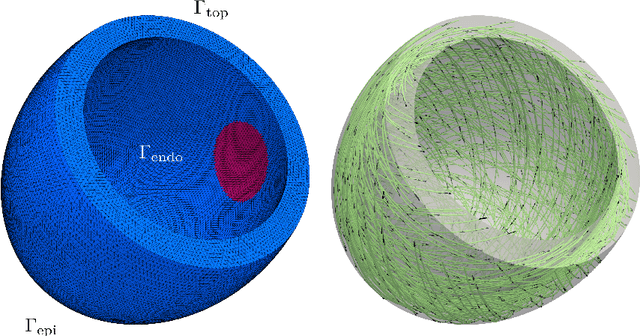
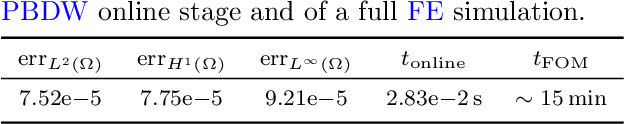
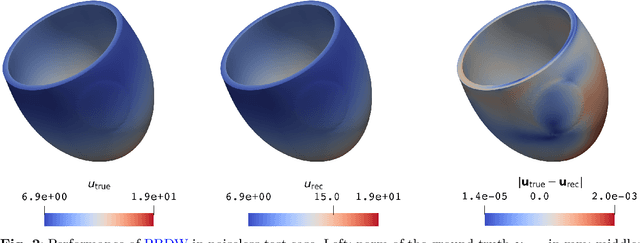
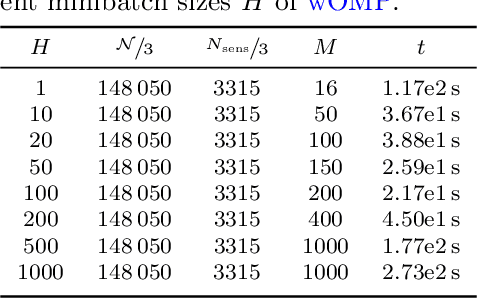
Abstract:Personalized cardiac diagnostics require accurate reconstruction of myocardial displacement fields from sparse clinical imaging data, yet current methods often demand intrusive access to computational models. In this work, we apply the non-intrusive Parametrized-Background Data-Weak (PBDW) approach to three-dimensional (3D) cardiac displacement field reconstruction from limited Magnetic Resonance Image (MRI)-like observations. Our implementation requires only solution snapshots -- no governing equations, assembly routines, or solver access -- enabling immediate deployment across commercial and research codes using different constitutive models. Additionally, we introduce two enhancements: an H-size minibatch worst-case Orthogonal Matching Pursuit (wOMP) algorithm that improves Sensor Selection (SS) computational efficiency while maintaining reconstruction accuracy, and memory optimization techniques exploiting block matrix structures in vectorial problems. We demonstrate the effectiveness of the method through validation on a 3D left ventricular model with simulated scar tissue. Starting with noise-free reconstruction, we systematically incorporate Gaussian noise and spatial sparsity mimicking realistic MRI acquisition protocols. Results show exceptional accuracy in noise-free conditions (relative L2 error of order O(1e-5)), robust performance with 10% noise (relative L2 error of order O(1e-2)), and effective reconstruction from sparse measurements (relative L2 error of order O(1e-2)). The online reconstruction achieves four-order-of-magnitude computational speed-up compared to full Finite Element (FE) simulations, with reconstruction times under one tenth of second for sparse scenarios, demonstrating significant potential for integration into clinical cardiac modeling workflows.
Physics-informed Neural Network Estimation of Material Properties in Soft Tissue Nonlinear Biomechanical Models
Dec 20, 2023Abstract:The development of biophysical models for clinical applications is rapidly advancing in the research community, thanks to their predictive nature and their ability to assist the interpretation of clinical data. However, high-resolution and accurate multi-physics computational models are computationally expensive and their personalisation involves fine calibration of a large number of parameters, which may be space-dependent, challenging their clinical translation. In this work, we propose a new approach which relies on the combination of physics-informed neural networks (PINNs) with three-dimensional soft tissue nonlinear biomechanical models, capable of reconstructing displacement fields and estimating heterogeneous patient-specific biophysical properties. The proposed learning algorithm encodes information from a limited amount of displacement and, in some cases, strain data, that can be routinely acquired in the clinical setting, and combines it with the physics of the problem, represented by a mathematical model based on partial differential equations, to regularise the problem and improve its convergence properties. Several benchmarks are presented to show the accuracy and robustness of the proposed method and its great potential to enable the robust and effective identification of patient-specific, heterogeneous physical properties, s.a. tissue stiffness properties. In particular, we demonstrate the capability of the PINN to detect the presence, location and severity of scar tissue, which is beneficial to develop personalised simulation models for disease diagnosis, especially for cardiac applications.
Shape of my heart: Cardiac models through learned signed distance functions
Sep 05, 2023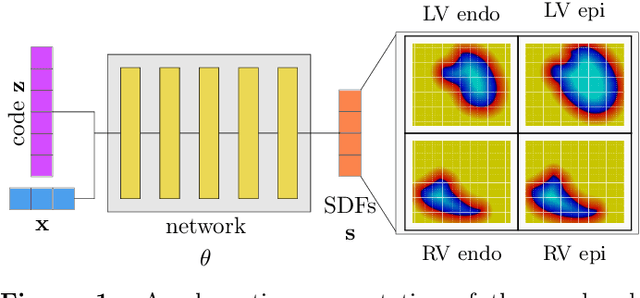
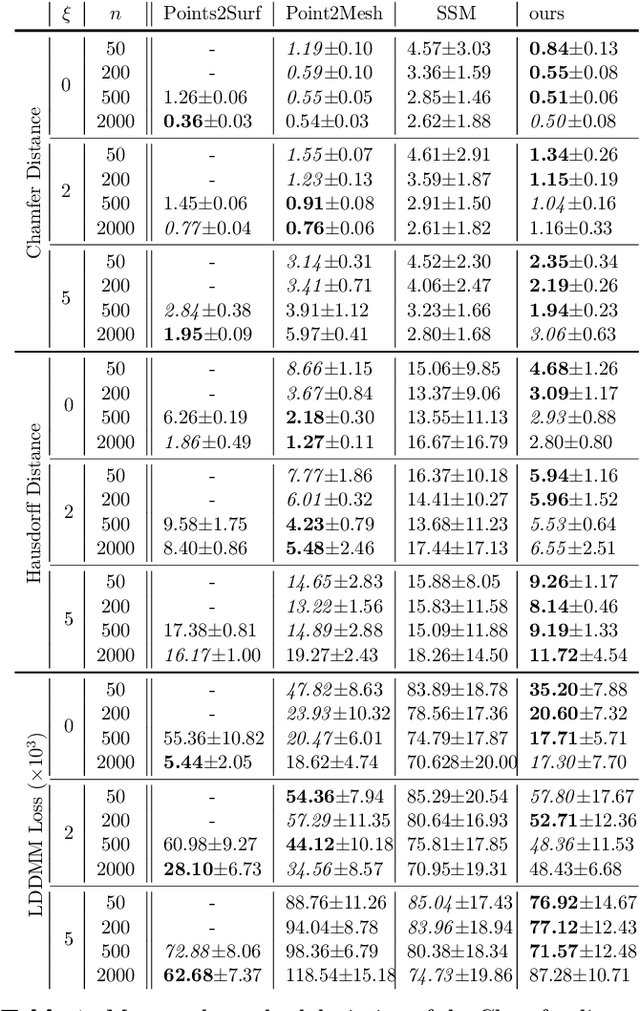
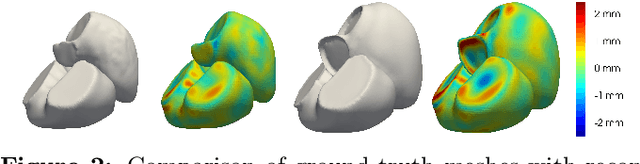
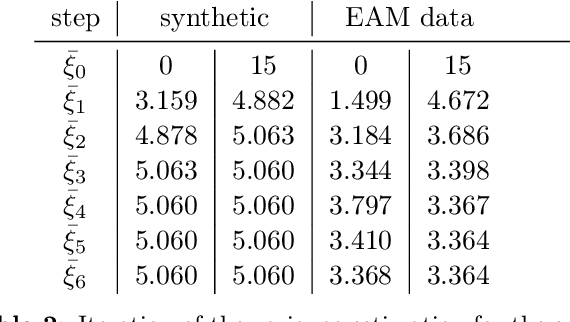
Abstract:The efficient construction of an anatomical model is one of the major challenges of patient-specific in-silico models of the human heart. Current methods frequently rely on linear statistical models, allowing no advanced topological changes, or requiring medical image segmentation followed by a meshing pipeline, which strongly depends on image resolution, quality, and modality. These approaches are therefore limited in their transferability to other imaging domains. In this work, the cardiac shape is reconstructed by means of three-dimensional deep signed distance functions with Lipschitz regularity. For this purpose, the shapes of cardiac MRI reconstructions are learned from public databases to model the spatial relation of multiple chambers in Cartesian space. We demonstrate that this approach is also capable of reconstructing anatomical models from partial data, such as point clouds from a single ventricle, or modalities different from the trained MRI, such as electroanatomical mapping, and in addition, allows us to generate new anatomical shapes by randomly sampling latent vectors.
Digital twinning of cardiac electrophysiology models from the surface ECG: a geodesic backpropagation approach
Aug 16, 2023Abstract:The eikonal equation has become an indispensable tool for modeling cardiac electrical activation accurately and efficiently. In principle, by matching clinically recorded and eikonal-based electrocardiograms (ECGs), it is possible to build patient-specific models of cardiac electrophysiology in a purely non-invasive manner. Nonetheless, the fitting procedure remains a challenging task. The present study introduces a novel method, Geodesic-BP, to solve the inverse eikonal problem. Geodesic-BP is well-suited for GPU-accelerated machine learning frameworks, allowing us to optimize the parameters of the eikonal equation to reproduce a given ECG. We show that Geodesic-BP can reconstruct a simulated cardiac activation with high accuracy in a synthetic test case, even in the presence of modeling inaccuracies. Furthermore, we apply our algorithm to a publicly available dataset of a rabbit model, with very positive results. Given the future shift towards personalized medicine, Geodesic-BP has the potential to help in future functionalizations of cardiac models meeting clinical time constraints while maintaining the physiological accuracy of state-of-the-art cardiac models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge