WarpPINN-fibers: improved cardiac strain estimation from cine-MR with physics-informed neural networks

The contractile motion of the heart is strongly determined by the distribution of the fibers that constitute cardiac tissue. Strain analysis informed with the orientation of fibers allows to describe several pathologies that are typically associated with impaired mechanics of the myocardium, such as cardiovascular disease. Several methods have been developed to estimate strain-derived metrics from traditional imaging techniques. However, the physical models underlying these methods do not include fiber mechanics, restricting their capacity to accurately explain cardiac function. In this work, we introduce WarpPINN-fibers, a physics-informed neural network framework to accurately obtain cardiac motion and strains enhanced by fiber information. We train our neural network to satisfy a hyper-elastic model and promote fiber contraction with the goal to predict the deformation field of the heart from cine magnetic resonance images. For this purpose, we build a loss function composed of three terms: a data-similarity loss between the reference and the warped template images, a regularizer enforcing near-incompressibility of cardiac tissue and a fiber-stretch penalization that controls strain in the direction of synthetically produced fibers. We show that our neural network improves the former WarpPINN model and effectively controls fiber stretch in a synthetic phantom experiment. Then, we demonstrate that WarpPINN-fibers outperforms alternative methodologies in landmark-tracking and strain curve prediction for a cine-MRI benchmark with a cohort of 15 healthy volunteers. We expect that our method will enable a more precise quantification of cardiac strains through accurate deformation fields that are consistent with fiber physiology, without requiring imaging techniques more sophisticated than MRI.

Fully data-driven inverse hyperelasticity with hyper-network neural ODE fields

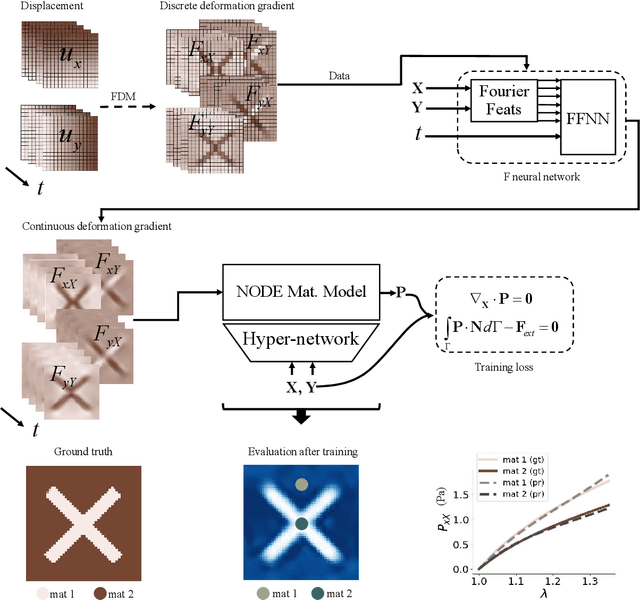
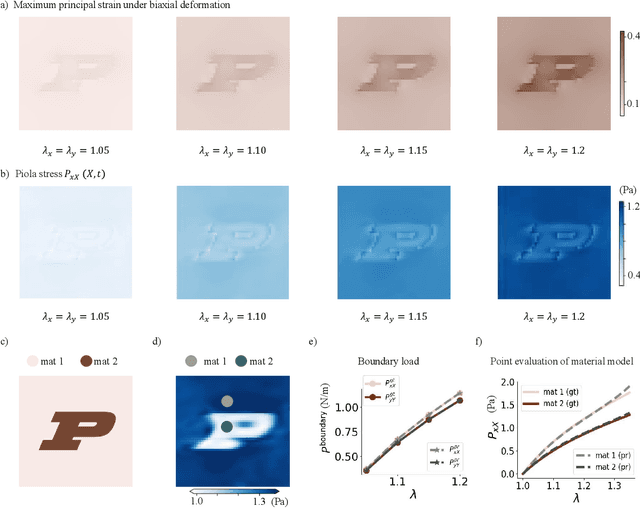
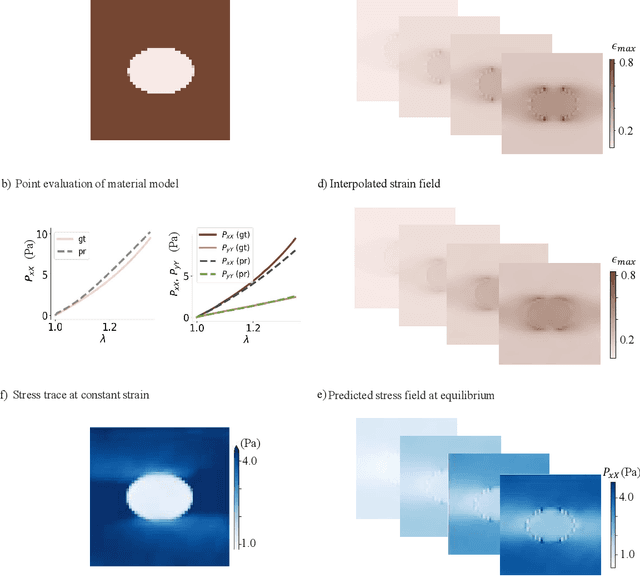
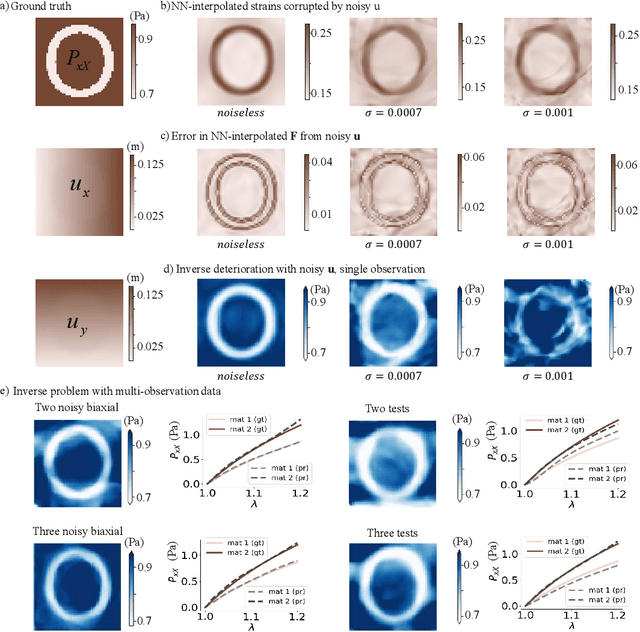
We propose a new framework for identifying mechanical properties of heterogeneous materials without a closed-form constitutive equation. Given a full-field measurement of the displacement field, for instance as obtained from digital image correlation (DIC), a continuous approximation of the strain field is obtained by training a neural network that incorporates Fourier features to effectively capture sharp gradients in the data. A physics-based data-driven method built upon ordinary neural differential equations (NODEs) is employed to discover constitutive equations. The NODE framework can represent arbitrary materials while satisfying constraints in the theory of constitutive equations by default. To account for heterogeneity, a hyper-network is defined, where the input is the material coordinate system, and the output is the NODE-based constitutive equation. The parameters of the hyper-network are optimized by minimizing a multi-objective loss function that includes penalty terms for violations of the strong form of the equilibrium equations of elasticity and the associated Neumann boundary conditions. We showcase the framework with several numerical examples, including heterogeneity arising from variations in material parameters, spatial transitions from isotropy to anisotropy, material identification in the presence of noise, and, ultimately, application to experimental data. As the numerical results suggest, the proposed approach is robust and general in identifying the mechanical properties of heterogeneous materials with very few assumptions, making it a suitable alternative to classical inverse methods.

Image Velocimetry using Direct Displacement Field estimation with Neural Networks for Fluids

An important tool for experimental fluids mechanics research is Particle Image Velocimetry (PIV). Several robust methodologies have been proposed to perform the estimation of velocity field from the images, however, alternative methods are still needed to increase the spatial resolution of the results. This work presents a novel approach for estimating fluid flow fields using neural networks and the optical flow equation to predict displacement vectors between sequential images. The result is a continuous representation of the displacement, that can be evaluated on the full spatial resolution of the image. The methodology was validated on synthetic and experimental images. Accurate results were obtained in terms of the estimation of instantaneous velocity fields, and of the determined time average turbulence quantities and power spectral density. The methodology proposed differs of previous attempts of using machine learning for this task: it does not require any previous training, and could be directly used in any pair of images.

PISCO: Self-Supervised k-Space Regularization for Improved Neural Implicit k-Space Representations of Dynamic MRI

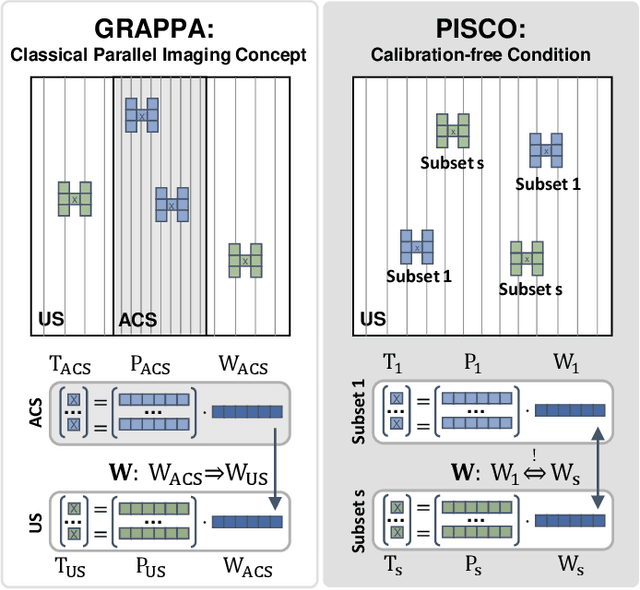
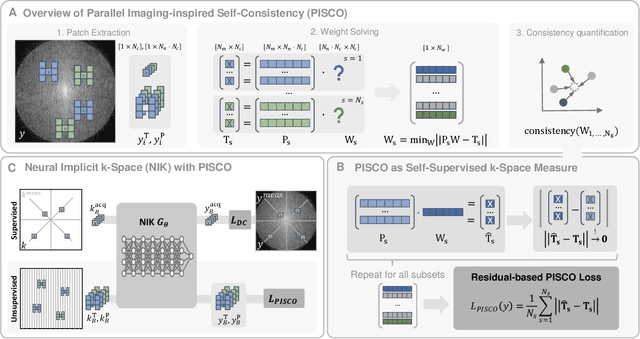
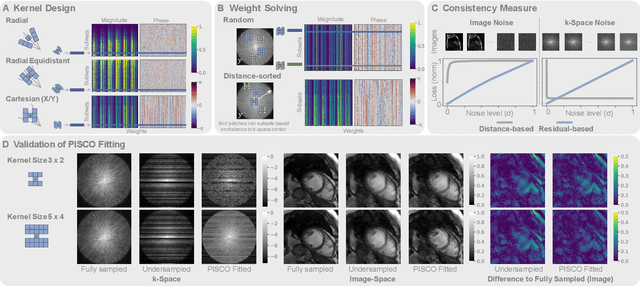
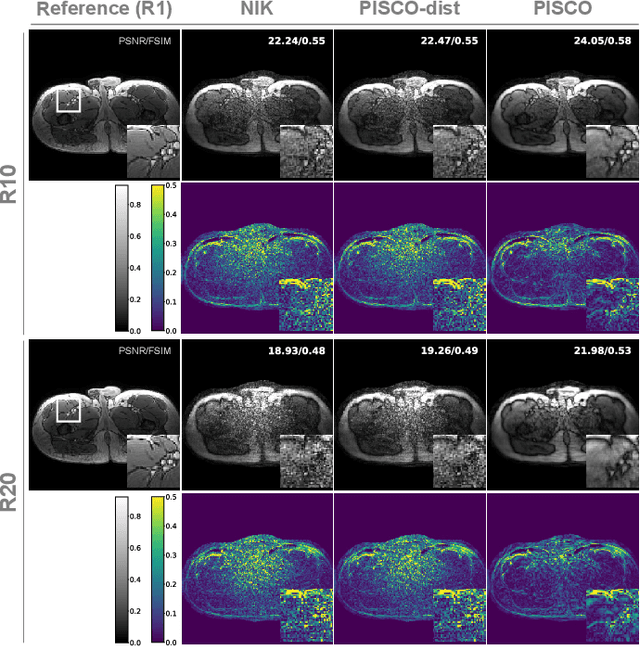
Neural implicit k-space representations (NIK) have shown promising results for dynamic magnetic resonance imaging (MRI) at high temporal resolutions. Yet, reducing acquisition time, and thereby available training data, results in severe performance drops due to overfitting. To address this, we introduce a novel self-supervised k-space loss function $\mathcal{L}_\mathrm{PISCO}$, applicable for regularization of NIK-based reconstructions. The proposed loss function is based on the concept of parallel imaging-inspired self-consistency (PISCO), enforcing a consistent global k-space neighborhood relationship without requiring additional data. Quantitative and qualitative evaluations on static and dynamic MR reconstructions show that integrating PISCO significantly improves NIK representations. Particularly for high acceleration factors (R$\geq$54), NIK with PISCO achieves superior spatio-temporal reconstruction quality compared to state-of-the-art methods. Furthermore, an extensive analysis of the loss assumptions and stability shows PISCO's potential as versatile self-supervised k-space loss function for further applications and architectures. Code is available at: https://github.com/compai-lab/2025-pisco-spieker

Ensemble learning of the atrial fiber orientation with physics-informed neural networks

The anisotropic structure of the myocardium is a key determinant of the cardiac function. To date, there is no imaging modality to assess in-vivo the cardiac fiber structure. We recently proposed Fibernet, a method for the automatic identification of the anisotropic conduction -- and thus fibers -- in the atria from local electrical recordings. Fibernet uses cardiac activation as recorded during electroanatomical mappings to infer local conduction properties using physics-informed neural networks. In this work, we extend Fibernet to cope with the uncertainty in the estimated fiber field. Specifically, we use an ensemble of neural networks to produce multiple samples, all fitting the observed data, and compute posterior statistics. We also introduce a methodology to select the best fiber orientation members and define the input of the neural networks directly on the atrial surface. With these improvements, we outperform the previous methodology in terms of fiber orientation error in 8 different atrial anatomies. Currently, our approach can estimate the fiber orientation and conduction velocities in under 7 minutes with quantified uncertainty, which opens the door to its application in clinical practice. We hope the proposed methodology will enable further personalization of cardiac digital twins for precision medicine.

Understanding the dynamics of the frequency bias in neural networks

Recent works have shown that traditional Neural Network (NN) architectures display a marked frequency bias in the learning process. Namely, the NN first learns the low-frequency features before learning the high-frequency ones. In this study, we rigorously develop a partial differential equation (PDE) that unravels the frequency dynamics of the error for a 2-layer NN in the Neural Tangent Kernel regime. Furthermore, using this insight, we explicitly demonstrate how an appropriate choice of distributions for the initialization weights can eliminate or control the frequency bias. We focus our study on the Fourier Features model, an NN where the first layer has sine and cosine activation functions, with frequencies sampled from a prescribed distribution. In this setup, we experimentally validate our theoretical results and compare the NN dynamics to the solution of the PDE using the finite element method. Finally, we empirically show that the same principle extends to multi-layer NNs.

Self-Supervised k-Space Regularization for Motion-Resolved Abdominal MRI Using Neural Implicit k-Space Representation

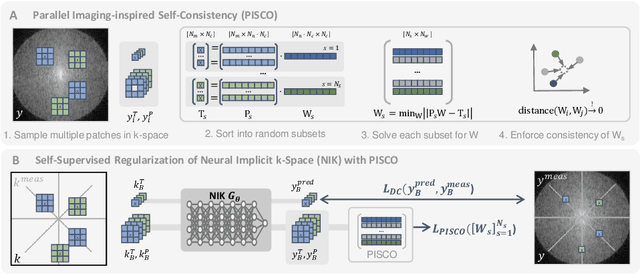
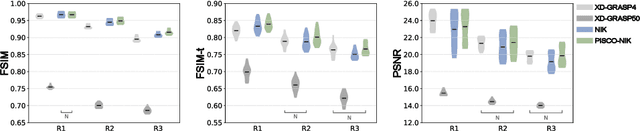
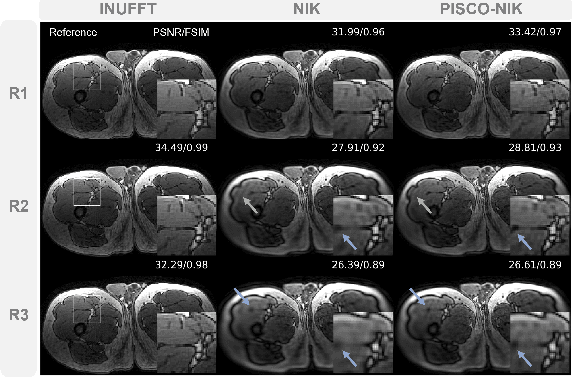
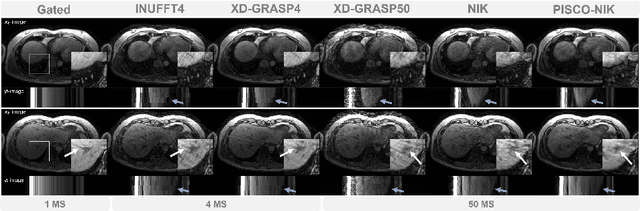
Neural implicit k-space representations have shown promising results for dynamic MRI at high temporal resolutions. Yet, their exclusive training in k-space limits the application of common image regularization methods to improve the final reconstruction. In this work, we introduce the concept of parallel imaging-inspired self-consistency (PISCO), which we incorporate as novel self-supervised k-space regularization enforcing a consistent neighborhood relationship. At no additional data cost, the proposed regularization significantly improves neural implicit k-space reconstructions on simulated data. Abdominal in-vivo reconstructions using PISCO result in enhanced spatio-temporal image quality compared to state-of-the-art methods. Code is available at https://github.com/vjspi/PISCO-NIK.

Probabilistic learning of the Purkinje network from the electrocardiogram

The identification of the Purkinje conduction system in the heart is a challenging task, yet essential for a correct definition of cardiac digital twins for precision cardiology. Here, we propose a probabilistic approach for identifying the Purkinje network from non-invasive clinical data such as the standard electrocardiogram (ECG). We use cardiac imaging to build an anatomically accurate model of the ventricles; we algorithmically generate a rule-based Purkinje network tailored to the anatomy; we simulate physiological electrocardiograms with a fast model; we identify the geometrical and electrical parameters of the Purkinje-ECG model with Bayesian optimization and approximate Bayesian computation. The proposed approach is inherently probabilistic and generates a population of plausible Purkinje networks, all fitting the ECG within a given tolerance. In this way, we can estimate the uncertainty of the parameters, thus providing reliable predictions. We test our methodology in physiological and pathological scenarios, showing that we are able to accurately recover the ECG with our model. We propagate the uncertainty in the Purkinje network parameters in a simulation of conduction system pacing therapy. Our methodology is a step forward in creation of digital twins from non-invasive data in precision medicine. An open source implementation can be found at http://github.com/fsahli/purkinje-learning

Shape of my heart: Cardiac models through learned signed distance functions

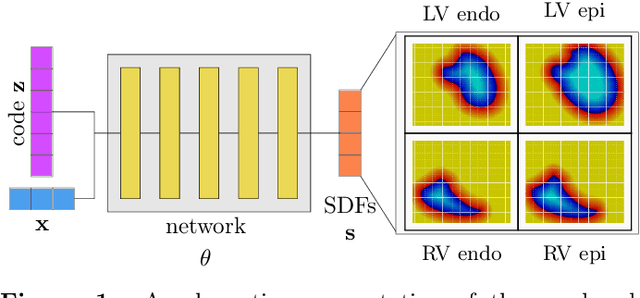
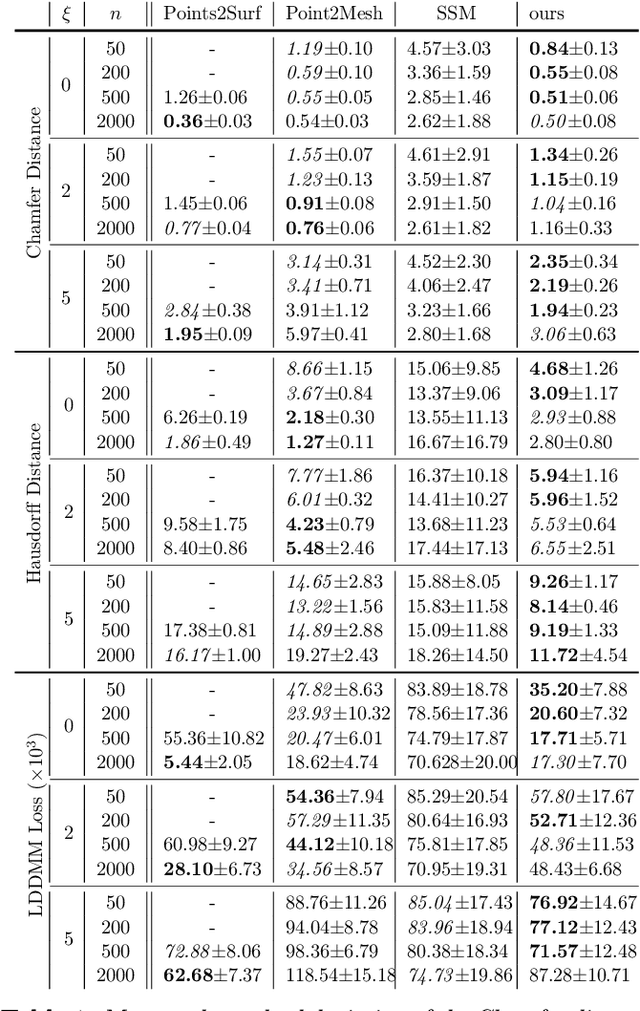
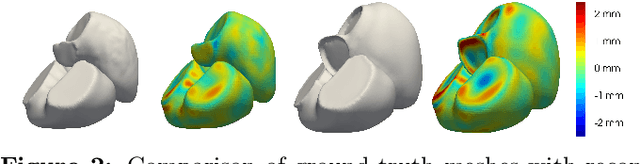
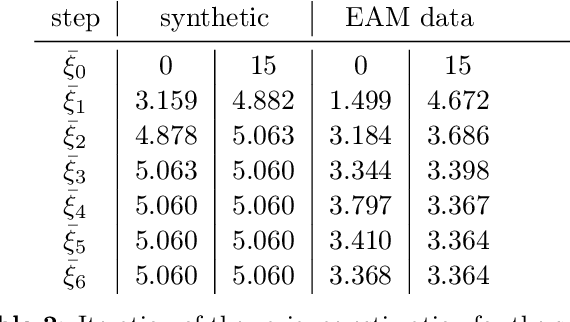
The efficient construction of an anatomical model is one of the major challenges of patient-specific in-silico models of the human heart. Current methods frequently rely on linear statistical models, allowing no advanced topological changes, or requiring medical image segmentation followed by a meshing pipeline, which strongly depends on image resolution, quality, and modality. These approaches are therefore limited in their transferability to other imaging domains. In this work, the cardiac shape is reconstructed by means of three-dimensional deep signed distance functions with Lipschitz regularity. For this purpose, the shapes of cardiac MRI reconstructions are learned from public databases to model the spatial relation of multiple chambers in Cartesian space. We demonstrate that this approach is also capable of reconstructing anatomical models from partial data, such as point clouds from a single ventricle, or modalities different from the trained MRI, such as electroanatomical mapping, and in addition, allows us to generate new anatomical shapes by randomly sampling latent vectors.

Physics-informed neural networks for blood flow inverse problems

Physics-informed neural networks (PINNs) have emerged as a powerful tool for solving inverse problems, especially in cases where no complete information about the system is known and scatter measurements are available. This is especially useful in hemodynamics since the boundary information is often difficult to model, and high-quality blood flow measurements are generally hard to obtain. In this work, we use the PINNs methodology for estimating reduced-order model parameters and the full velocity field from scatter 2D noisy measurements in the ascending aorta. The results show stable and accurate parameter estimations when using the method with simulated data, while the velocity reconstruction shows dependence on the measurement quality and the flow pattern complexity. The method allows for solving clinical-relevant inverse problems in hemodynamics and complex coupled physical systems.