Fully data-driven inverse hyperelasticity with hyper-network neural ODE fields

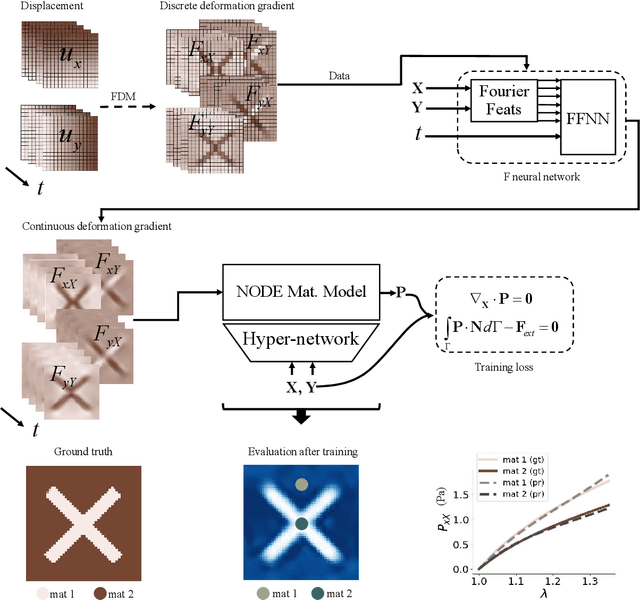
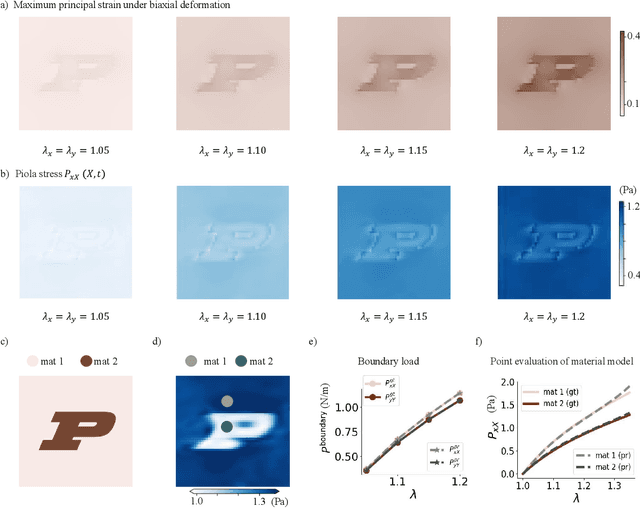
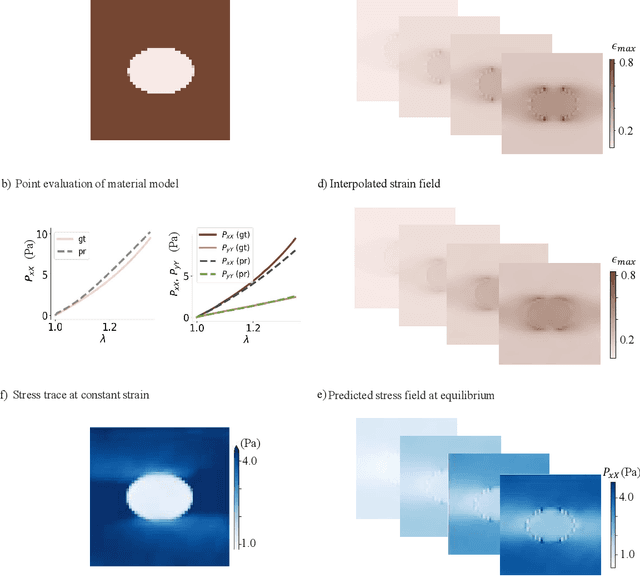
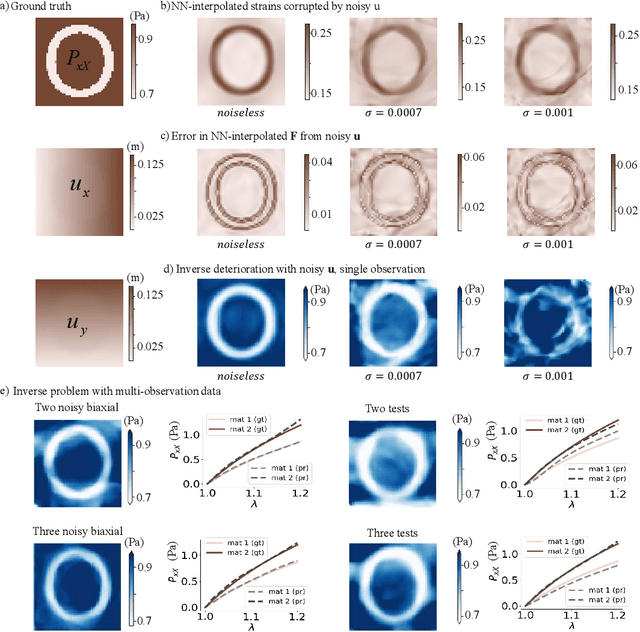
We propose a new framework for identifying mechanical properties of heterogeneous materials without a closed-form constitutive equation. Given a full-field measurement of the displacement field, for instance as obtained from digital image correlation (DIC), a continuous approximation of the strain field is obtained by training a neural network that incorporates Fourier features to effectively capture sharp gradients in the data. A physics-based data-driven method built upon ordinary neural differential equations (NODEs) is employed to discover constitutive equations. The NODE framework can represent arbitrary materials while satisfying constraints in the theory of constitutive equations by default. To account for heterogeneity, a hyper-network is defined, where the input is the material coordinate system, and the output is the NODE-based constitutive equation. The parameters of the hyper-network are optimized by minimizing a multi-objective loss function that includes penalty terms for violations of the strong form of the equilibrium equations of elasticity and the associated Neumann boundary conditions. We showcase the framework with several numerical examples, including heterogeneity arising from variations in material parameters, spatial transitions from isotropy to anisotropy, material identification in the presence of noise, and, ultimately, application to experimental data. As the numerical results suggest, the proposed approach is robust and general in identifying the mechanical properties of heterogeneous materials with very few assumptions, making it a suitable alternative to classical inverse methods.

Automatically Polyconvex Strain Energy Functions using Neural Ordinary Differential Equations

Data-driven methods are becoming an essential part of computational mechanics due to their unique advantages over traditional material modeling. Deep neural networks are able to learn complex material response without the constraints of closed-form approximations. However, imposing the physics-based mathematical requirements that any material model must comply with is not straightforward for data-driven approaches. In this study, we use a novel class of neural networks, known as neural ordinary differential equations (N-ODEs), to develop data-driven material models that automatically satisfy polyconvexity of the strain energy function with respect to the deformation gradient, a condition needed for the existence of minimizers for boundary value problems in elasticity. We take advantage of the properties of ordinary differential equations to create monotonic functions that approximate the derivatives of the strain energy function with respect to the invariants of the right Cauchy-Green deformation tensor. The monotonicity of the derivatives guarantees the convexity of the energy. The N-ODE material model is able to capture synthetic data generated from closed-form material models, and it outperforms conventional models when tested against experimental data on skin, a highly nonlinear and anisotropic material. We also showcase the use of the N-ODE material model in finite element simulations. The framework is general and can be used to model a large class of materials. Here we focus on hyperelasticity, but polyconvex strain energies are a core building block for other problems in elasticity such as viscous and plastic deformations. We therefore expect our methodology to further enable data-driven methods in computational mechanics

Predicting the Mechanical Properties of Fibrin Using Neural Networks Trained on Discrete Fiber Network Data

Fibrin is a structural protein key for processes such as wound healing and thrombus formation. At the macroscale, fibrin forms a gel and has a mechanical response that is dictated by the mechanics of a microscale fiber network. Hence, accurate description of fibrin gels can be achieved using representative volume elements (RVE) that explicitly model the discrete fiber networks of the microscale. These RVE models, however, cannot be efficiently used to model the macroscale due to the challenges and computational demands of multiscale coupling. Here, we propose the use of an artificial, fully connected neural network (FCNN) to efficiently capture the behavior of the RVE models. The FCNN was trained on 1100 fiber networks subjected to 121 biaxial deformations. The stress data from the RVE, together with the total energy on the fibers and the condition of incompressibility of the surrounding matrix, were used to determine the derivatives of an unknown strain energy function with respect to the deformation invariants. During training, the loss function was modified to ensure convexity of the strain energy function and symmetry of its Hessian. A general FCNN model was coded into a user material subroutine (UMAT) in the software Abaqus. The UMAT implementation takes in the structure and parameters of an arbitrary FCNN as material parameters from the input file. The inputs to the FCNN include the first two isochoric invariants of the deformation. The FCNN outputs the derivatives of the strain energy with respect to the isochoric invariants. In this work, the FCNN trained on the discrete fiber network data was used in finite element simulations of fibrin gels using our UMAT. We anticipate that this work will enable further integration of machine learning tools with computational mechanics. It will also improve computational modeling of biological materials characterized by a multiscale structure.

Improving Reconstructive Surgery Design using Gaussian Process Surrogates to Capture Material Behavior Uncertainty

Excessive loads near wounds produce pathological scarring and other complications. Presently, stress cannot easily be measured by surgeons in the operating room. Instead, surgeons rely on intuition and experience. Predictive computational tools are ideal candidates for surgery planning. Finite element (FE) simulations have shown promise in predicting stress fields on large skin patches and complex cases, helping to identify potential regions of complication. Unfortunately, these simulations are computationally expensive and deterministic. However, running a few, well-selected FE simulations allows us to create Gaussian process (GP) surrogate models of local cutaneous flaps that are computationally efficient and able to predict stress and strain for arbitrary material parameters. Here, we create GP surrogates for the advancement, rotation, and transposition flaps. We then use the predictive capability of these surrogates to perform a global sensitivity analysis, ultimately showing that fiber direction has the most significant impact on strain field variations. We then perform an optimization to determine the optimal fiber direction for each flap for three different objectives driven by clinical guidelines. While material properties are not controlled by the surgeon and are actually a source of uncertainty, the surgeon can in fact control the orientation of the flap. Therefore, fiber direction is the only material parameter that can be optimized clinically. The optimization task relies on the efficiency of the GP surrogates to calculate the expected cost of different strategies when the uncertainty of other material parameters is included. We propose optimal flap orientations for the three cost functions and that can help in reducing stress resulting from the surgery and ultimately reduce complications associated with excessive mechanical loading near wounds.