A Causal Graph-Enhanced Gaussian Process Regression for Modeling Engine-out NOx

The stringent regulatory requirements on nitrogen oxides (NOx) emissions from diesel compression ignition engines require accurate and reliable models for real-time monitoring and diagnostics. Although traditional methods such as physical sensors and virtual engine control module (ECM) sensors provide essential data, they are only used for estimation. Ubiquitous literature primarily focuses on deterministic models with little emphasis on capturing the uncertainties due to sensors. The lack of probabilistic frameworks restricts the applicability of these models for robust diagnostics. The objective of this paper is to develop and validate a probabilistic model to predict engine-out NOx emissions using Gaussian process regression. Our approach is as follows. We employ three variants of Gaussian process models: the first with a standard radial basis function kernel with input window, the second incorporating a deep kernel using convolutional neural networks to capture temporal dependencies, and the third enriching the deep kernel with a causal graph derived via graph convolutional networks. The causal graph embeds physics knowledge into the learning process. All models are compared against a virtual ECM sensor using both quantitative and qualitative metrics. We conclude that our model provides an improvement in predictive performance when using an input window and a deep kernel structure. Even more compelling is the further enhancement achieved by the incorporation of a causal graph into the deep kernel. These findings are corroborated across different validation datasets.

Neural information field filter

We introduce neural information field filter, a Bayesian state and parameter estimation method for high-dimensional nonlinear dynamical systems given large measurement datasets. Solving such a problem using traditional methods, such as Kalman and particle filters, is computationally expensive. Information field theory is a Bayesian approach that can efficiently reconstruct dynamical model state paths and calibrate model parameters from noisy measurement data. To apply the method, we parameterize the time evolution state path using the span of a finite linear basis. The existing method has to reparameterize the state path by initial states to satisfy the initial condition. Designing an expressive yet simple linear basis before knowing the true state path is crucial for inference accuracy but challenging. Moreover, reparameterizing the state path using the initial state is easy to perform for a linear basis, but is nontrivial for more complex and expressive function parameterizations, such as neural networks. The objective of this paper is to simplify and enrich the class of state path parameterizations using neural networks for the information field theory approach. To this end, we propose a generalized physics-informed conditional prior using an auxiliary initial state. We show the existing reparameterization is a special case. We parameterize the state path using a residual neural network that consists of a linear basis function and a Fourier encoding fully connected neural network residual function. The residual function aims to correct the error of the linear basis function. To sample from the intractable posterior distribution, we develop an optimization algorithm, nested stochastic variational inference, and a sampling algorithm, nested preconditioned stochastic gradient Langevin dynamics. A series of numerical and experimental examples verify and validate the proposed method.

An information field theory approach to Bayesian state and parameter estimation in dynamical systems

Dynamical system state estimation and parameter calibration problems are ubiquitous across science and engineering. Bayesian approaches to the problem are the gold standard as they allow for the quantification of uncertainties and enable the seamless fusion of different experimental modalities. When the dynamics are discrete and stochastic, one may employ powerful techniques such as Kalman, particle, or variational filters. Practitioners commonly apply these methods to continuous-time, deterministic dynamical systems after discretizing the dynamics and introducing fictitious transition probabilities. However, approaches based on time-discretization suffer from the curse of dimensionality since the number of random variables grows linearly with the number of time-steps. Furthermore, the introduction of fictitious transition probabilities is an unsatisfactory solution because it increases the number of model parameters and may lead to inference bias. To address these drawbacks, the objective of this paper is to develop a scalable Bayesian approach to state and parameter estimation suitable for continuous-time, deterministic dynamical systems. Our methodology builds upon information field theory. Specifically, we construct a physics-informed prior probability measure on the function space of system responses so that functions that satisfy the physics are more likely. This prior allows us to quantify model form errors. We connect the system's response to observations through a probabilistic model of the measurement process. The joint posterior over the system responses and all parameters is given by Bayes' rule. To approximate the intractable posterior, we develop a stochastic variational inference algorithm. In summary, the developed methodology offers a powerful framework for Bayesian estimation in dynamical systems.

Learning to solve Bayesian inverse problems: An amortized variational inference approach

Inverse problems, i.e., estimating parameters of physical models from experimental data, are ubiquitous in science and engineering. The Bayesian formulation is the gold standard because it alleviates ill-posedness issues and quantifies epistemic uncertainty. Since analytical posteriors are not typically available, one resorts to Markov chain Monte Carlo sampling or approximate variational inference. However, inference needs to be rerun from scratch for each new set of data. This drawback limits the applicability of the Bayesian formulation to real-time settings, e.g., health monitoring of engineered systems, and medical diagnosis. The objective of this paper is to develop a methodology that enables real-time inference by learning the Bayesian inverse map, i.e., the map from data to posteriors. Our approach is as follows. We represent the posterior distribution using a parameterization based on deep neural networks. Next, we learn the network parameters by amortized variational inference method which involves maximizing the expectation of evidence lower bound over all possible datasets compatible with the model. We demonstrate our approach by solving examples a set of benchmark problems from science and engineering. Our results show that the posterior estimates of our approach are in agreement with the corresponding ground truth obtained by Markov chain Monte Carlo. Once trained, our approach provides the posterior parameters of observation just at the cost of a forward pass of the neural network.

Physics-informed Information Field Theory for Modeling Physical Systems with Uncertainty Quantification

Data-driven approaches coupled with physical knowledge are powerful techniques to model systems. The goal of such models is to efficiently solve for the underlying field by combining measurements with known physical laws. As many systems contain unknown elements, such as missing parameters, noisy data, or incomplete physical laws, this is widely approached as an uncertainty quantification problem. The common techniques to handle all the variables typically depend on the numerical scheme used to approximate the posterior, and it is desirable to have a method which is independent of any such discretization. Information field theory (IFT) provides the tools necessary to perform statistics over fields that are not necessarily Gaussian. We extend IFT to physics-informed IFT (PIFT) by encoding the functional priors with information about the physical laws which describe the field. The posteriors derived from this PIFT remain independent of any numerical scheme and can capture multiple modes, allowing for the solution of problems which are ill-posed. We demonstrate our approach through an analytical example involving the Klein-Gordon equation. We then develop a variant of stochastic gradient Langevin dynamics to draw samples from the joint posterior over the field and model parameters. We apply our method to numerical examples with various degrees of model-form error and to inverse problems involving nonlinear differential equations. As an addendum, the method is equipped with a metric which allows the posterior to automatically quantify model-form uncertainty. Because of this, our numerical experiments show that the method remains robust to even an incorrect representation of the physics given sufficient data. We numerically demonstrate that the method correctly identifies when the physics cannot be trusted, in which case it automatically treats learning the field as a regression problem.

Physics-informed neural networks for solving parametric magnetostatic problems

The optimal design of magnetic devices becomes intractable using current computational methods when the number of design parameters is high. The emerging physics-informed deep learning framework has the potential to alleviate this curse of dimensionality. The objective of this paper is to investigate the ability of physics-informed neural networks to learn the magnetic field response as a function of design parameters in the context of a two-dimensional (2-D) magnetostatic problem. Our approach is as follows. We derive the variational principle for 2-D parametric magnetostatic problems, and prove the existence and uniqueness of the solution that satisfies the equations of the governing physics, i.e., Maxwell's equations. We use a deep neural network (DNN) to represent the magnetic field as a function of space and a total of ten parameters that describe geometric features and operating point conditions. We train the DNN by minimizing the physics-informed loss function using a variant of stochastic gradient descent. Subsequently, we conduct systematic numerical studies using a parametric EI-core electromagnet problem. In these studies, we vary the DNN architecture trying more than one hundred different possibilities. For each study, we evaluate the accuracy of the DNN by comparing its predictions to those of finite element analysis. In an exhaustive non-parametric study, we observe that sufficiently parameterized dense networks result in relative errors of less than 1%. Residual connections always improve relative errors for the same number of training iterations. Also, we observe that Fourier encoding features aligned with the device geometry do improve the rate of convergence, albeit higher-order harmonics are not necessary. Finally, we demonstrate our approach on a ten-dimensional problem with parameterized geometry.

Bayesian Model Averaging for Data Driven Decision Making when Causality is Partially Known

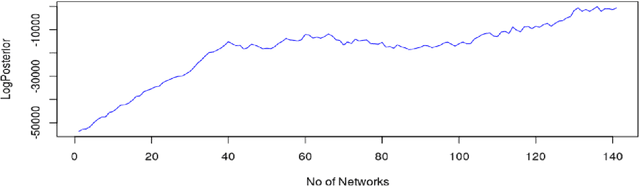
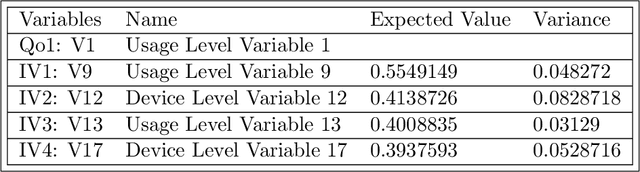
Probabilistic machine learning models are often insufficient to help with decisions on interventions because those models find correlations - not causal relationships. If observational data is only available and experimentation are infeasible, the correct approach to study the impact of an intervention is to invoke Pearl's causality framework. Even that framework assumes that the underlying causal graph is known, which is seldom the case in practice. When the causal structure is not known, one may use out-of-the-box algorithms to find causal dependencies from observational data. However, there exists no method that also accounts for the decision-maker's prior knowledge when developing the causal structure either. The objective of this paper is to develop rational approaches for making decisions from observational data in the presence of causal graph uncertainty and prior knowledge from the decision-maker. We use ensemble methods like Bayesian Model Averaging (BMA) to infer set of causal graphs that can represent the data generation process. We provide decisions by computing the expected value and risk of potential interventions explicitly. We demonstrate our approach by applying them in different example contexts.

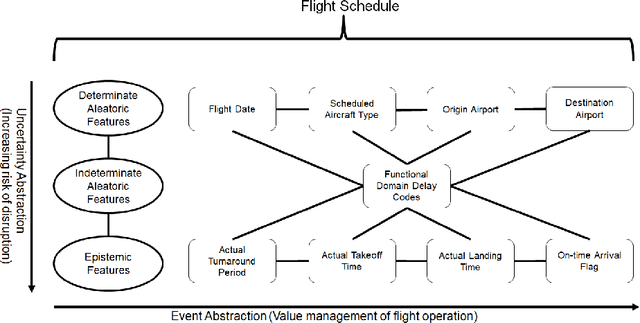
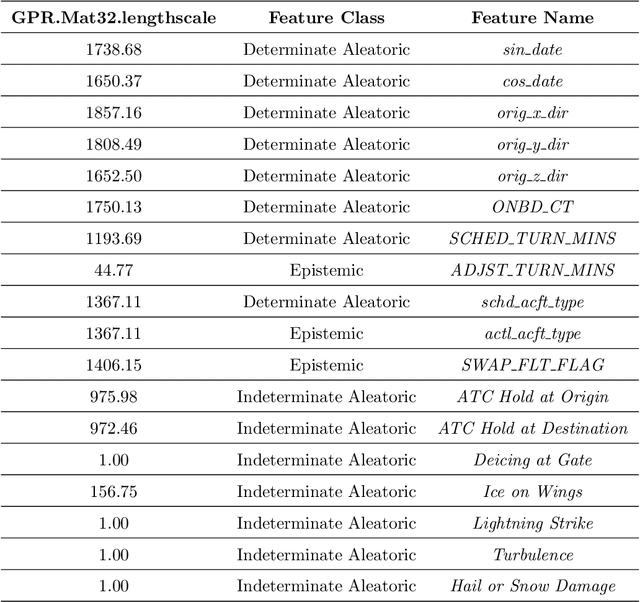
Exploratory Data Analysis for Airline Disruption Management

Reliable platforms for data collation during airline schedule operations have significantly increased the quality and quantity of available information for effectively managing airline schedule disruptions. To that effect, this paper applies macroscopic and microscopic techniques by way of basic statistics and machine learning, respectively, to analyze historical scheduling and operations data from a major airline in the United States. Macroscopic results reveal that majority of irregular operations in airline schedule that occurred over a one-year period stemmed from disruptions due to flight delays, while microscopic results validate different modeling assumptions about key drivers for airline disruption management like turnaround as a Gaussian process.

Improving Reconstructive Surgery Design using Gaussian Process Surrogates to Capture Material Behavior Uncertainty

Excessive loads near wounds produce pathological scarring and other complications. Presently, stress cannot easily be measured by surgeons in the operating room. Instead, surgeons rely on intuition and experience. Predictive computational tools are ideal candidates for surgery planning. Finite element (FE) simulations have shown promise in predicting stress fields on large skin patches and complex cases, helping to identify potential regions of complication. Unfortunately, these simulations are computationally expensive and deterministic. However, running a few, well-selected FE simulations allows us to create Gaussian process (GP) surrogate models of local cutaneous flaps that are computationally efficient and able to predict stress and strain for arbitrary material parameters. Here, we create GP surrogates for the advancement, rotation, and transposition flaps. We then use the predictive capability of these surrogates to perform a global sensitivity analysis, ultimately showing that fiber direction has the most significant impact on strain field variations. We then perform an optimization to determine the optimal fiber direction for each flap for three different objectives driven by clinical guidelines. While material properties are not controlled by the surgeon and are actually a source of uncertainty, the surgeon can in fact control the orientation of the flap. Therefore, fiber direction is the only material parameter that can be optimized clinically. The optimization task relies on the efficiency of the GP surrogates to calculate the expected cost of different strategies when the uncertainty of other material parameters is included. We propose optimal flap orientations for the three cost functions and that can help in reducing stress resulting from the surgery and ultimately reduce complications associated with excessive mechanical loading near wounds.

Learning Arbitrary Quantities of Interest from Expensive Black-Box Functions through Bayesian Sequential Optimal Design

Estimating arbitrary quantities of interest (QoIs) that are non-linear operators of complex, expensive-to-evaluate, black-box functions is a challenging problem due to missing domain knowledge and finite budgets. Bayesian optimal design of experiments (BODE) is a family of methods that identify an optimal design of experiments (DOE) under different contexts, using only in a limited number of function evaluations. Under BODE methods, sequential design of experiments (SDOE) accomplishes this task by selecting an optimal sequence of experiments while using data-driven probabilistic surrogate models instead of the expensive black-box function. Probabilistic predictions from the surrogate model are used to define an information acquisition function (IAF) which quantifies the marginal value contributed or the expected information gained by a hypothetical experiment. The next experiment is selected by maximizing the IAF. A generally applicable IAF is the expected information gain (EIG) about a QoI as captured by the expectation of the Kullback-Leibler divergence between the predictive distribution of the QoI after doing a hypothetical experiment and the current predictive distribution about the same QoI. We model the underlying information source as a fully-Bayesian, non-stationary Gaussian process (FBNSGP), and derive an approximation of the information gain of a hypothetical experiment about an arbitrary QoI conditional on the hyper-parameters The EIG about the same QoI is estimated by sample averages to integrate over the posterior of the hyper-parameters and the potential experimental outcomes. We demonstrate the performance of our method in four numerical examples and a practical engineering problem of steel wire manufacturing. The method is compared to two classic SDOE methods: random sampling and uncertainty sampling.