Learning Arbitrary Quantities of Interest from Expensive Black-Box Functions through Bayesian Sequential Optimal Design

Estimating arbitrary quantities of interest (QoIs) that are non-linear operators of complex, expensive-to-evaluate, black-box functions is a challenging problem due to missing domain knowledge and finite budgets. Bayesian optimal design of experiments (BODE) is a family of methods that identify an optimal design of experiments (DOE) under different contexts, using only in a limited number of function evaluations. Under BODE methods, sequential design of experiments (SDOE) accomplishes this task by selecting an optimal sequence of experiments while using data-driven probabilistic surrogate models instead of the expensive black-box function. Probabilistic predictions from the surrogate model are used to define an information acquisition function (IAF) which quantifies the marginal value contributed or the expected information gained by a hypothetical experiment. The next experiment is selected by maximizing the IAF. A generally applicable IAF is the expected information gain (EIG) about a QoI as captured by the expectation of the Kullback-Leibler divergence between the predictive distribution of the QoI after doing a hypothetical experiment and the current predictive distribution about the same QoI. We model the underlying information source as a fully-Bayesian, non-stationary Gaussian process (FBNSGP), and derive an approximation of the information gain of a hypothetical experiment about an arbitrary QoI conditional on the hyper-parameters The EIG about the same QoI is estimated by sample averages to integrate over the posterior of the hyper-parameters and the potential experimental outcomes. We demonstrate the performance of our method in four numerical examples and a practical engineering problem of steel wire manufacturing. The method is compared to two classic SDOE methods: random sampling and uncertainty sampling.

Learning Personalized Thermal Preferences via Bayesian Active Learning with Unimodality Constraints

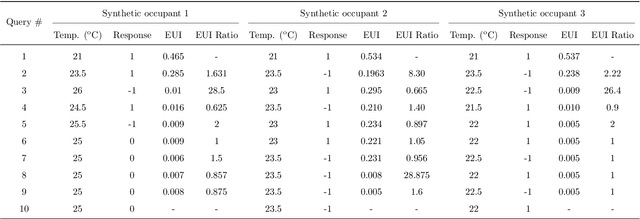
Thermal preferences vary from person to person and may change over time. The main objective of this paper is to sequentially pose intelligent queries to occupants in order to optimally learn the indoor air temperature values which maximize their satisfaction. Our central hypothesis is that an occupant's preference relation over indoor air temperature can be described using a scalar function of these temperatures, which we call the "occupant's thermal utility function". Information about an occupant's preference over these temperatures is available to us through their response to thermal preference queries : "prefer warmer," "prefer cooler" and "satisfied" which we interpret as statements about the derivative of their utility function, i.e. the utility function is "increasing", "decreasing" and "constant" respectively. We model this hidden utility function using a Gaussian process prior with built-in unimodality constraint, i.e., the utility function has a unique maximum, and we train this model using Bayesian inference. This permits an expected improvement based selection of next preference query to pose to the occupant, which takes into account both exploration (sampling from areas of high uncertainty) and exploitation (sampling from areas which are likely to offer an improvement over current best observation). We use this framework to sequentially design experiments and illustrate its benefits by showing that it requires drastically fewer observations to learn the maximally preferred temperature values as compared to other methods. This framework is an important step towards the development of intelligent HVAC systems which would be able to respond to occupants' personalized thermal comfort needs. In order to encourage the use of our PE framework and ensure reproducibility in results, we publish an implementation of our work named GPPrefElicit as an open-source package in Python.