On-Board Vision-Language Models for Personalized Autonomous Vehicle Motion Control: System Design and Real-World Validation

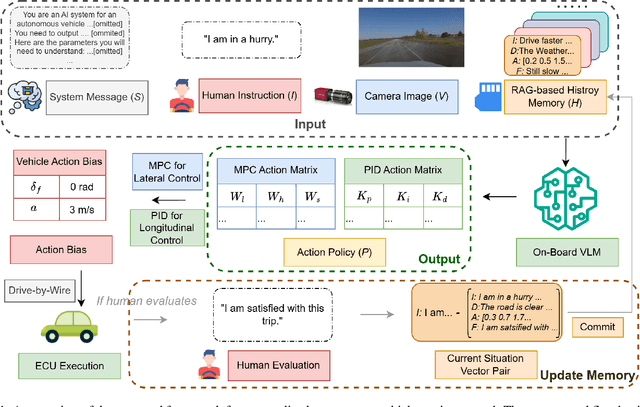
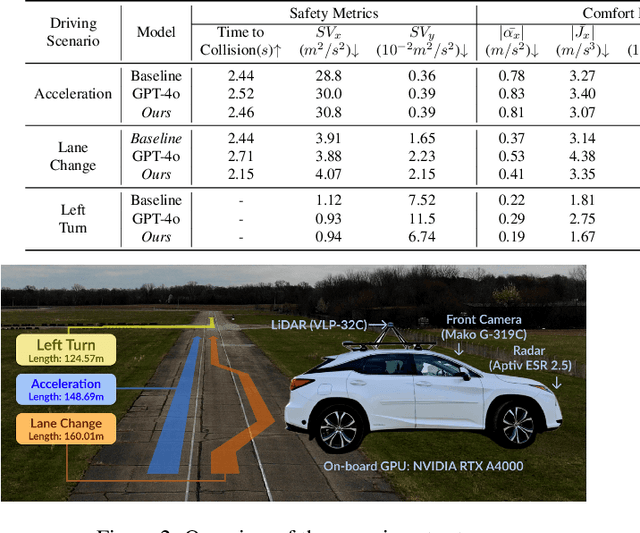
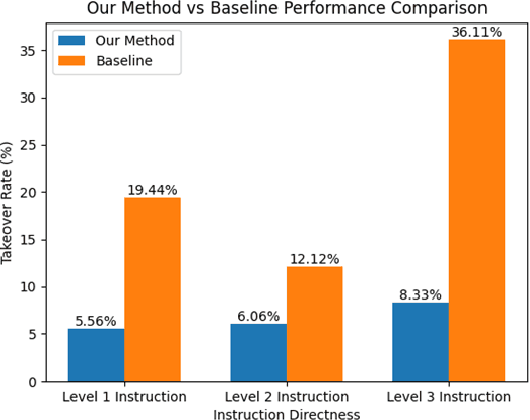
Personalized driving refers to an autonomous vehicle's ability to adapt its driving behavior or control strategies to match individual users' preferences and driving styles while maintaining safety and comfort standards. However, existing works either fail to capture every individual preference precisely or become computationally inefficient as the user base expands. Vision-Language Models (VLMs) offer promising solutions to this front through their natural language understanding and scene reasoning capabilities. In this work, we propose a lightweight yet effective on-board VLM framework that provides low-latency personalized driving performance while maintaining strong reasoning capabilities. Our solution incorporates a Retrieval-Augmented Generation (RAG)-based memory module that enables continuous learning of individual driving preferences through human feedback. Through comprehensive real-world vehicle deployment and experiments, our system has demonstrated the ability to provide safe, comfortable, and personalized driving experiences across various scenarios and significantly reduce takeover rates by up to 76.9%. To the best of our knowledge, this work represents the first end-to-end VLM-based motion control system in real-world autonomous vehicles.

Learning Arbitrary Quantities of Interest from Expensive Black-Box Functions through Bayesian Sequential Optimal Design

Estimating arbitrary quantities of interest (QoIs) that are non-linear operators of complex, expensive-to-evaluate, black-box functions is a challenging problem due to missing domain knowledge and finite budgets. Bayesian optimal design of experiments (BODE) is a family of methods that identify an optimal design of experiments (DOE) under different contexts, using only in a limited number of function evaluations. Under BODE methods, sequential design of experiments (SDOE) accomplishes this task by selecting an optimal sequence of experiments while using data-driven probabilistic surrogate models instead of the expensive black-box function. Probabilistic predictions from the surrogate model are used to define an information acquisition function (IAF) which quantifies the marginal value contributed or the expected information gained by a hypothetical experiment. The next experiment is selected by maximizing the IAF. A generally applicable IAF is the expected information gain (EIG) about a QoI as captured by the expectation of the Kullback-Leibler divergence between the predictive distribution of the QoI after doing a hypothetical experiment and the current predictive distribution about the same QoI. We model the underlying information source as a fully-Bayesian, non-stationary Gaussian process (FBNSGP), and derive an approximation of the information gain of a hypothetical experiment about an arbitrary QoI conditional on the hyper-parameters The EIG about the same QoI is estimated by sample averages to integrate over the posterior of the hyper-parameters and the potential experimental outcomes. We demonstrate the performance of our method in four numerical examples and a practical engineering problem of steel wire manufacturing. The method is compared to two classic SDOE methods: random sampling and uncertainty sampling.

Deriving Information Acquisition Criteria For Sequentially Inferring The Expected Value Of A Black-Box Function

Acquiring information about noisy expensive black-box functions (computer simulations or physical experiments) is a tremendously challenging problem. Finite computational and financial resources restrict the application of traditional methods for design of experiments. The problem is surmounted by hurdles such as numerical errors and stochastic approximations errors, when the quantity of interest (QoI) in a problem depends on an expensive black-box function. Bayesian optimal design of experiments has been reasonably successful in guiding the designer towards the QoI for problems of the above kind. This is usually achieved by sequentially querying the function at designs selected by an infill-sampling criterion compatible with utility theory. However, most current methods are semantically designed to work only on optimizing or inferring the black-box function itself. We aim to construct a heuristic which can unequivocally deal with the above problems irrespective of the QoI. This paper applies the above mentioned heuristic to infer a specific QoI, namely the expectation (expected value) of the function. The Kullback Leibler (KL) divergence is fairly conspicuous among techniques that used to quantify information gain. In this paper, we derive an expression for the expected KL divergence to sequentially infer our QoI. The analytical tractability provided by the Karhunene Loeve expansion around the Gaussian process (GP) representation of the black-box function allows circumvention around numerical issues associated with sample averaging. The proposed methodology can be extended to any QoI, with reasonable assumptions. The proposed method is verified and validated on three synthetic functions with varying levels of complexity and dimensionality. We demonstrate our methodology on a steel wire manufacturing problem.