Heterogenous Multi-Source Data Fusion Through Input Mapping and Latent Variable Gaussian Process

Artificial intelligence and machine learning frameworks have served as computationally efficient mapping between inputs and outputs for engineering problems. These mappings have enabled optimization and analysis routines that have warranted superior designs, ingenious material systems and optimized manufacturing processes. A common occurrence in such modeling endeavors is the existence of multiple source of data, each differentiated by fidelity, operating conditions, experimental conditions, and more. Data fusion frameworks have opened the possibility of combining such differentiated sources into single unified models, enabling improved accuracy and knowledge transfer. However, these frameworks encounter limitations when the different sources are heterogeneous in nature, i.e., not sharing the same input parameter space. These heterogeneous input scenarios can occur when the domains differentiated by complexity, scale, and fidelity require different parametrizations. Towards addressing this void, a heterogeneous multi-source data fusion framework is proposed based on input mapping calibration (IMC) and latent variable Gaussian process (LVGP). In the first stage, the IMC algorithm is utilized to transform the heterogeneous input parameter spaces into a unified reference parameter space. In the second stage, a multi-source data fusion model enabled by LVGP is leveraged to build a single source-aware surrogate model on the transformed reference space. The proposed framework is demonstrated and analyzed on three engineering case studies (design of cantilever beam, design of ellipsoidal void and modeling properties of Ti6Al4V alloy). The results indicate that the proposed framework provides improved predictive accuracy over a single source model and transformed but source unaware model.

Interpretable Multi-Source Data Fusion Through Latent Variable Gaussian Process

With the advent of artificial intelligence (AI) and machine learning (ML), various domains of science and engineering communites has leveraged data-driven surrogates to model complex systems from numerous sources of information (data). The proliferation has led to significant reduction in cost and time involved in development of superior systems designed to perform specific functionalities. A high proposition of such surrogates are built extensively fusing multiple sources of data, may it be published papers, patents, open repositories, or other resources. However, not much attention has been paid to the differences in quality and comprehensiveness of the known and unknown underlying physical parameters of the information sources that could have downstream implications during system optimization. Towards resolving this issue, a multi-source data fusion framework based on Latent Variable Gaussian Process (LVGP) is proposed. The individual data sources are tagged as a characteristic categorical variable that are mapped into a physically interpretable latent space, allowing the development of source-aware data fusion modeling. Additionally, a dissimilarity metric based on the latent variables of LVGP is introduced to study and understand the differences in the sources of data. The proposed approach is demonstrated on and analyzed through two mathematical (representative parabola problem, 2D Ackley function) and two materials science (design of FeCrAl and SmCoFe alloys) case studies. From the case studies, it is observed that compared to using single-source and source unaware ML models, the proposed multi-source data fusion framework can provide better predictions for sparse-data problems, interpretability regarding the sources, and enhanced modeling capabilities by taking advantage of the correlations and relationships among different sources.

Application of probabilistic modeling and automated machine learning framework for high-dimensional stress field

Modern computational methods, involving highly sophisticated mathematical formulations, enable several tasks like modeling complex physical phenomenon, predicting key properties and design optimization. The higher fidelity in these computer models makes it computationally intensive to query them hundreds of times for optimization and one usually relies on a simplified model albeit at the cost of losing predictive accuracy and precision. Towards this, data-driven surrogate modeling methods have shown a lot of promise in emulating the behavior of the expensive computer models. However, a major bottleneck in such methods is the inability to deal with high input dimensionality and the need for relatively large datasets. With such problems, the input and output quantity of interest are tensors of high dimensionality. Commonly used surrogate modeling methods for such problems, suffer from requirements like high number of computational evaluations that precludes one from performing other numerical tasks like uncertainty quantification and statistical analysis. In this work, we propose an end-to-end approach that maps a high-dimensional image like input to an output of high dimensionality or its key statistics. Our approach uses two main framework that perform three steps: a) reduce the input and output from a high-dimensional space to a reduced or low-dimensional space, b) model the input-output relationship in the low-dimensional space, and c) enable the incorporation of domain-specific physical constraints as masks. In order to accomplish the task of reducing input dimensionality we leverage principal component analysis, that is coupled with two surrogate modeling methods namely: a) Bayesian hybrid modeling, and b) DeepHyper's deep neural networks. We demonstrate the applicability of the approach on a problem of a linear elastic stress field data.

Reinforcement Learning based Sequential Batch-sampling for Bayesian Optimal Experimental Design

Engineering problems that are modeled using sophisticated mathematical methods or are characterized by expensive-to-conduct tests or experiments, are encumbered with limited budget or finite computational resources. Moreover, practical scenarios in the industry, impose restrictions, based on logistics and preference, on the manner in which the experiments can be conducted. For example, material supply may enable only a handful of experiments in a single-shot or in the case of computational models one may face significant wait-time based on shared computational resources. In such scenarios, one usually resorts to performing experiments in a manner that allows for maximizing one's state-of-knowledge while satisfying the above mentioned practical constraints. Sequential design of experiments (SDOE) is a popular suite of methods, that has yielded promising results in recent years across different engineering and practical problems. A common strategy, that leverages Bayesian formalism is the Bayesian SDOE, which usually works best in the one-step-ahead or myopic scenario of selecting a single experiment at each step of a sequence of experiments. In this work, we aim to extend the SDOE strategy, to query the experiment or computer code at a batch of inputs. To this end, we leverage deep reinforcement learning (RL) based policy gradient methods, to propose batches of queries that are selected taking into account entire budget in hand. The algorithm retains the sequential nature, inherent in the SDOE, while incorporating elements of reward based on task from the domain of deep RL. A unique capability of the proposed methodology is its ability to be applied to multiple tasks, for example optimization of a function, once its trained. We demonstrate the performance of the proposed algorithm on a synthetic problem, and a challenging high-dimensional engineering problem.

Inverse Aerodynamic Design of Gas Turbine Blades using Probabilistic Machine Learning

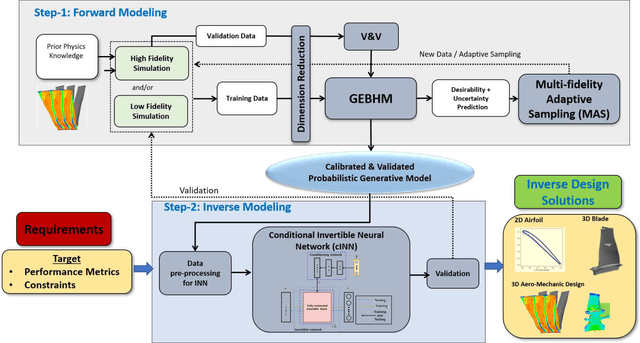
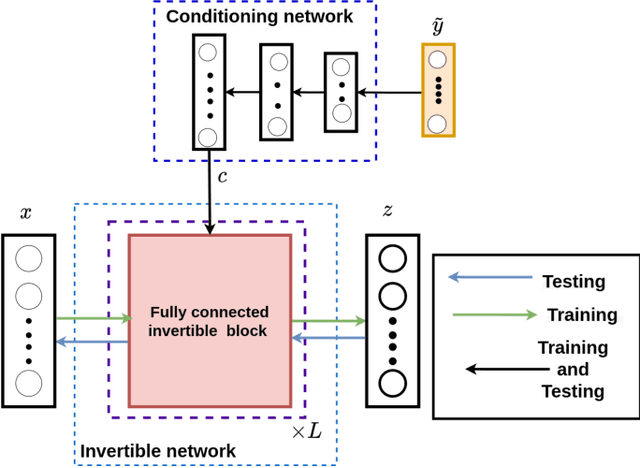
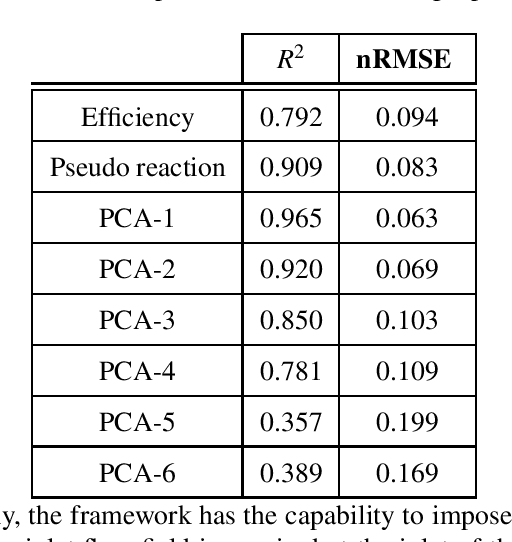
One of the critical components in Industrial Gas Turbines (IGT) is the turbine blade. Design of turbine blades needs to consider multiple aspects like aerodynamic efficiency, durability, safety and manufacturing, which make the design process sequential and iterative.The sequential nature of these iterations forces a long design cycle time, ranging from several months to years. Due to the reactionary nature of these iterations, little effort has been made to accumulate data in a manner that allows for deep exploration and understanding of the total design space. This is exemplified in the process of designing the individual components of the IGT resulting in a potential unrealized efficiency. To overcome the aforementioned challenges, we demonstrate a probabilistic inverse design machine learning framework (PMI), to carry out an explicit inverse design. PMI calculates the design explicitly without excessive costly iteration and overcomes the challenges associated with ill-posed inverse problems. In this work, the framework will be demonstrated on inverse aerodynamic design of three-dimensional turbine blades.

Data-based Discovery of Governing Equations

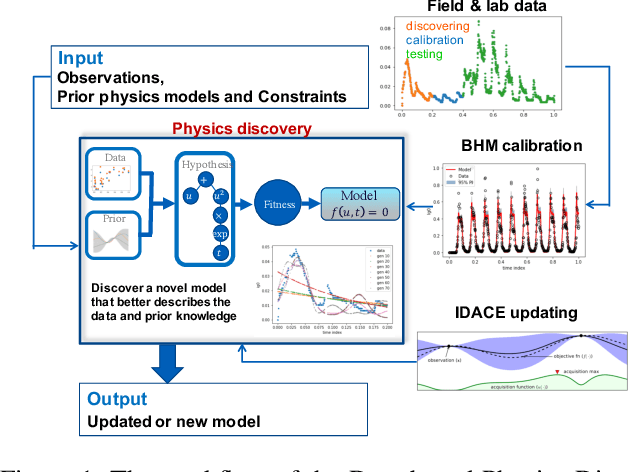
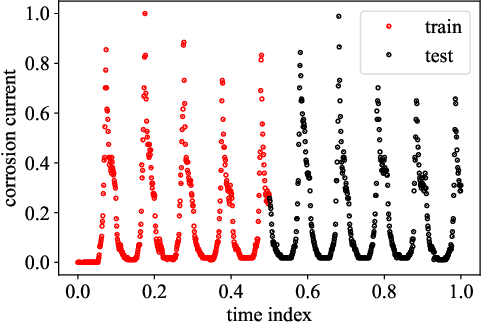
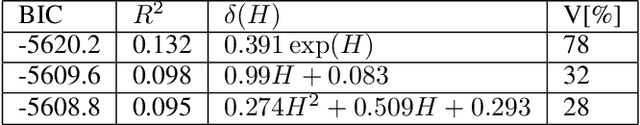
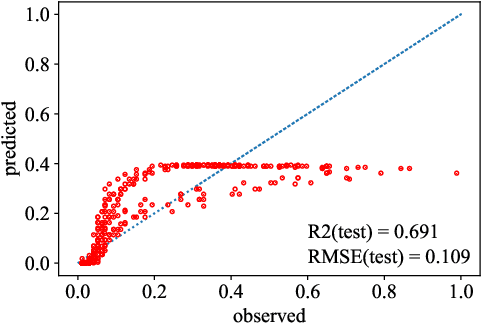
Most common mechanistic models are traditionally presented in mathematical forms to explain a given physical phenomenon. Machine learning algorithms, on the other hand, provide a mechanism to map the input data to output without explicitly describing the underlying physical process that generated the data. We propose a Data-based Physics Discovery (DPD) framework for automatic discovery of governing equations from observed data. Without a prior definition of the model structure, first a free-form of the equation is discovered, and then calibrated and validated against the available data. In addition to the observed data, the DPD framework can utilize available prior physical models, and domain expert feedback. When prior models are available, the DPD framework can discover an additive or multiplicative correction term represented symbolically. The correction term can be a function of the existing input variable to the prior model, or a newly introduced variable. In case a prior model is not available, the DPD framework discovers a new data-based standalone model governing the observations. We demonstrate the performance of the proposed framework on a real-world application in the aerospace industry.

Data-Informed Decomposition for Localized Uncertainty Quantification of Dynamical Systems

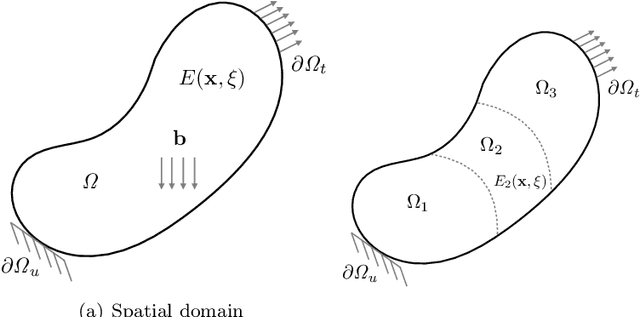
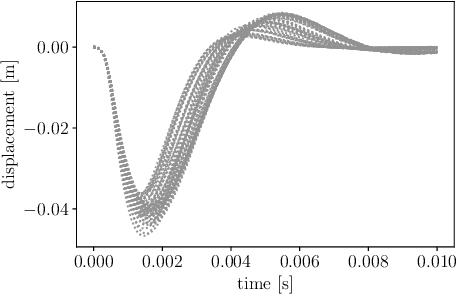
Industrial dynamical systems often exhibit multi-scale response due to material heterogeneities, operation conditions and complex environmental loadings. In such problems, it is the case that the smallest length-scale of the systems dynamics controls the numerical resolution required to effectively resolve the embedded physics. In practice however, high numerical resolutions is only required in a confined region of the system where fast dynamics or localized material variability are exhibited, whereas a coarser discretization can be sufficient in the rest majority of the system. To this end, a unified computational scheme with uniform spatio-temporal resolutions for uncertainty quantification can be very computationally demanding. Partitioning the complex dynamical system into smaller easier-to-solve problems based of the localized dynamics and material variability can reduce the overall computational cost. However, identifying the region of interest for high-resolution and intensive uncertainty quantification can be a problem dependent. The region of interest can be specified based on the localization features of the solution, user interest, and correlation length of the random material properties. For problems where a region of interest is not evident, Bayesian inference can provide a feasible solution. In this work, we employ a Bayesian framework to update our prior knowledge on the localized region of interest using measurements and system response. To address the computational cost of the Bayesian inference, we construct a Gaussian process surrogate for the forward model. Once, the localized region of interest is identified, we use polynomial chaos expansion to propagate the localization uncertainty. We demonstrate our framework through numerical experiments on a three-dimensional elastodynamic problem.

A Fully Bayesian Gradient-Free Supervised Dimension Reduction Method using Gaussian Processes

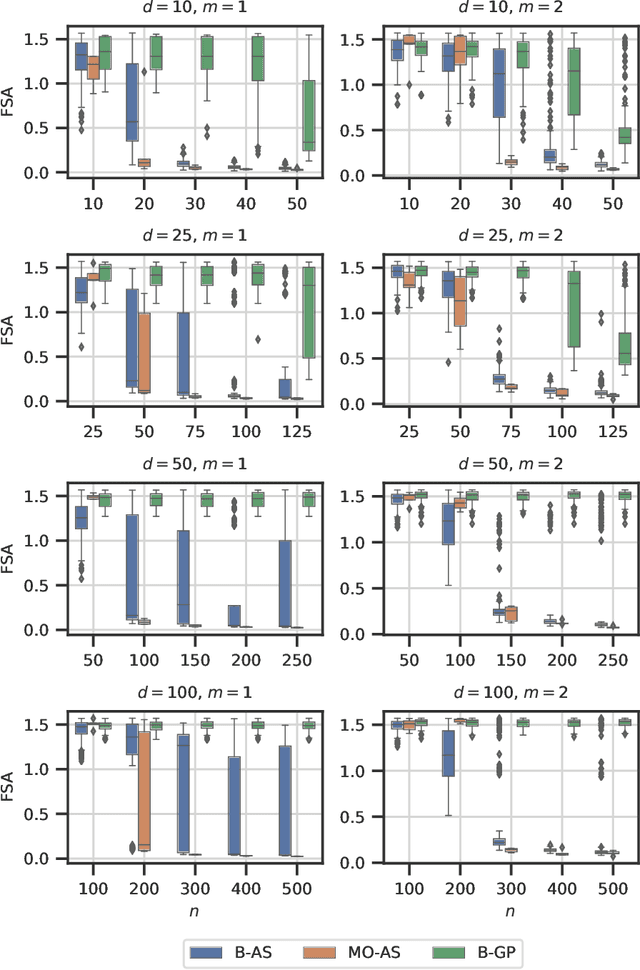
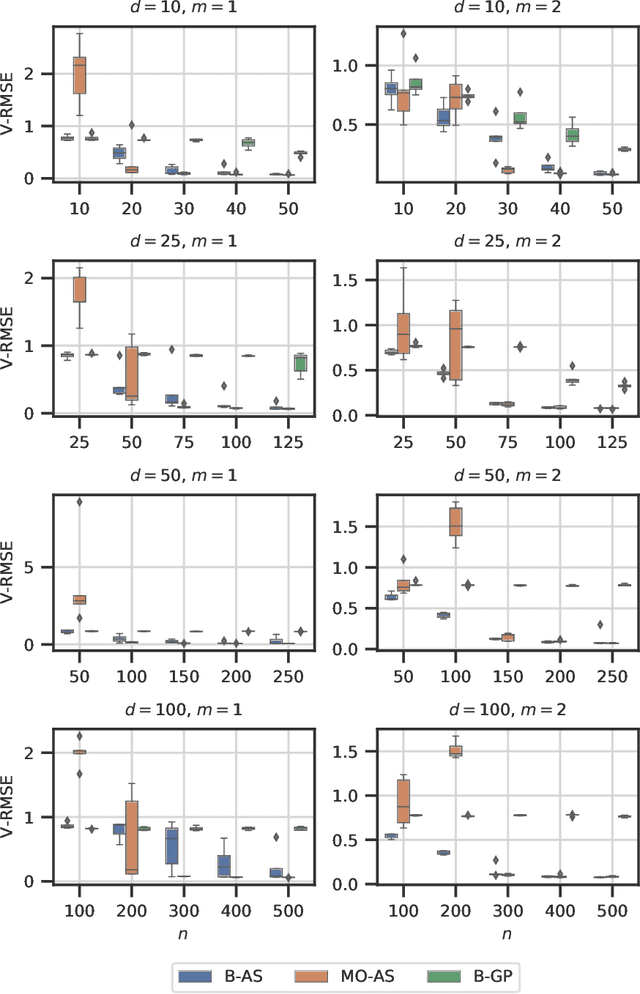
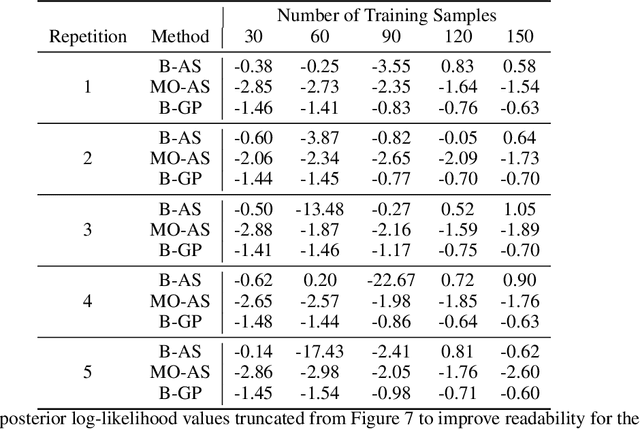
Modern day engineering problems are ubiquitously characterized by sophisticated computer codes that map parameters or inputs to an underlying physical process. In other situations, experimental setups are used to model the physical process in a laboratory, ensuring high precision while being costly in materials and logistics. In both scenarios, only limited amount of data can be generated by querying the expensive information source at a finite number of inputs or designs. This problem is compounded further in the presence of a high-dimensional input space. State-of-the-art parameter space dimension reduction methods, such as active subspace, aim to identify a subspace of the original input space that is sufficient to explain the output response. These methods are restricted by their reliance on gradient evaluations or copious data, making them inadequate to expensive problems without direct access to gradients. The proposed methodology is gradient-free and fully Bayesian, as it quantifies uncertainty in both the low-dimensional subspace and the surrogate model parameters. This enables a full quantification of epistemic uncertainty and robustness to limited data availability. It is validated on multiple datasets from engineering and science and compared to two other state-of-the-art methods based on four aspects: a) recovery of the active subspace, b) deterministic prediction accuracy, c) probabilistic prediction accuracy, and d) training time. The comparison shows that the proposed method improves the active subspace recovery and predictive accuracy, in both the deterministic and probabilistic sense, when only few model observations are available for training, at the cost of increased training time.

Bayesian learning of orthogonal embeddings for multi-fidelity Gaussian Processes

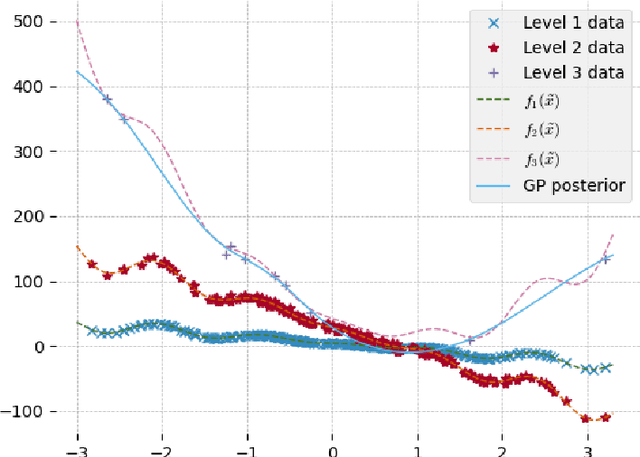
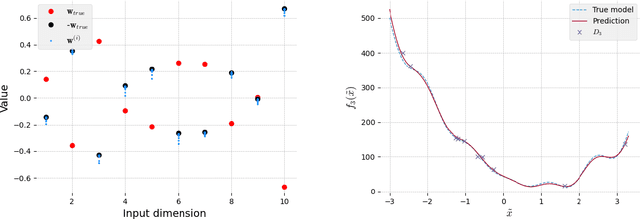
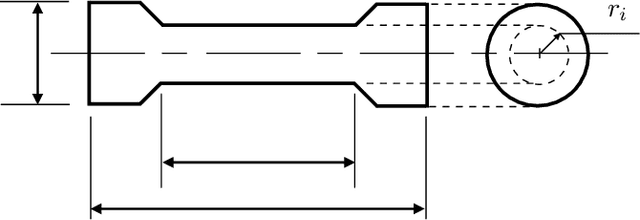
We present a Bayesian approach to identify optimal transformations that map model input points to low dimensional latent variables. The "projection" mapping consists of an orthonormal matrix that is considered a priori unknown and needs to be inferred jointly with the GP parameters, conditioned on the available training data. The proposed Bayesian inference scheme relies on a two-step iterative algorithm that samples from the marginal posteriors of the GP parameters and the projection matrix respectively, both using Markov Chain Monte Carlo (MCMC) sampling. In order to take into account the orthogonality constraints imposed on the orthonormal projection matrix, a Geodesic Monte Carlo sampling algorithm is employed, that is suitable for exploiting probability measures on manifolds. We extend the proposed framework to multi-fidelity models using GPs including the scenarios of training multiple outputs together. We validate our framework on three synthetic problems with a known lower-dimensional subspace. The benefits of our proposed framework, are illustrated on the computationally challenging three-dimensional aerodynamic optimization of a last-stage blade for an industrial gas turbine, where we study the effect of an 85-dimensional airfoil shape parameterization on two output quantities of interest, specifically on the aerodynamic efficiency and the degree of reaction.

Advances in Bayesian Probabilistic Modeling for Industrial Applications

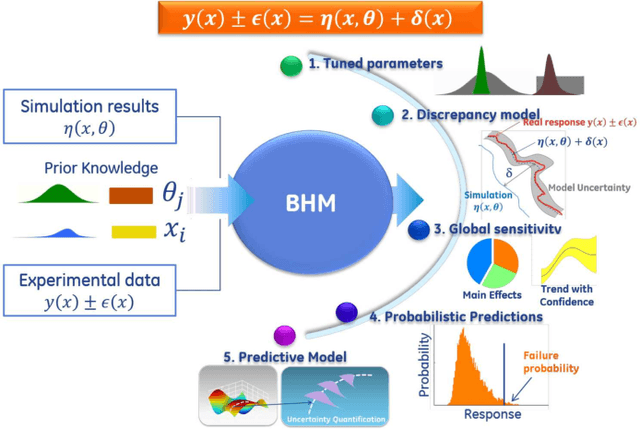
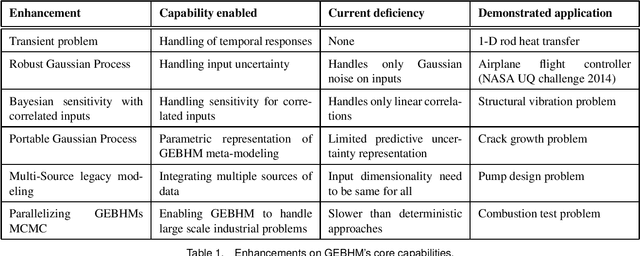
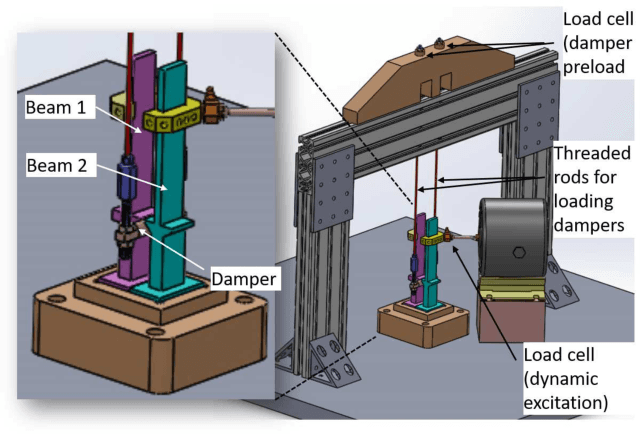
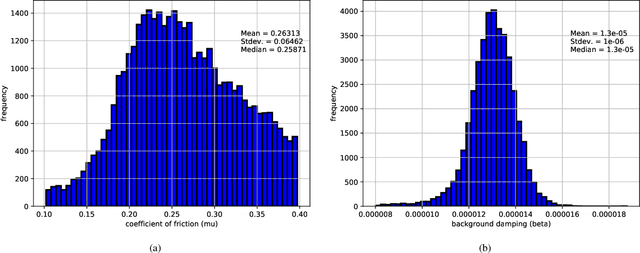
Industrial applications frequently pose a notorious challenge for state-of-the-art methods in the contexts of optimization, designing experiments and modeling unknown physical response. This problem is aggravated by limited availability of clean data, uncertainty in available physics-based models and additional logistic and computational expense associated with experiments. In such a scenario, Bayesian methods have played an impactful role in alleviating the aforementioned obstacles by quantifying uncertainty of different types under limited resources. These methods, usually deployed as a framework, allows decision makers to make informed choices under uncertainty while being able to incorporate information on the the fly, usually in the form of data, from multiple sources while being consistent with the physical intuition about the problem. This is a major advantage that Bayesian methods bring to fruition especially in the industrial context. This paper is a compendium of the Bayesian modeling methodology that is being consistently developed at GE Research. The methodology, called GE's Bayesian Hybrid Modeling (GEBHM), is a probabilistic modeling method, based on the Kennedy and O'Hagan framework, that has been continuously scaled-up and industrialized over several years. In this work, we explain the various advancements in GEBHM's methods and demonstrate their impact on several challenging industrial problems.