Data-based Discovery of Governing Equations

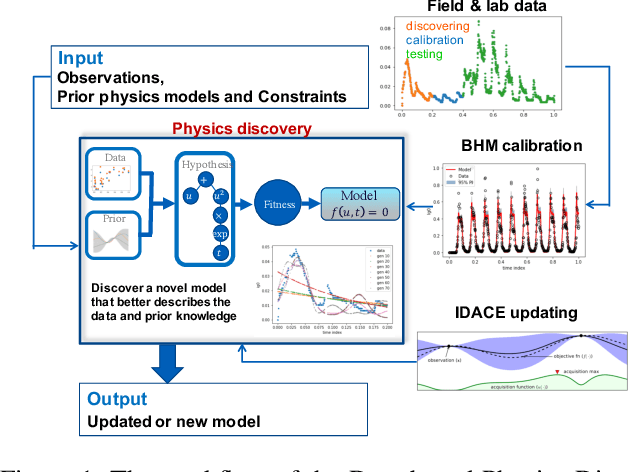
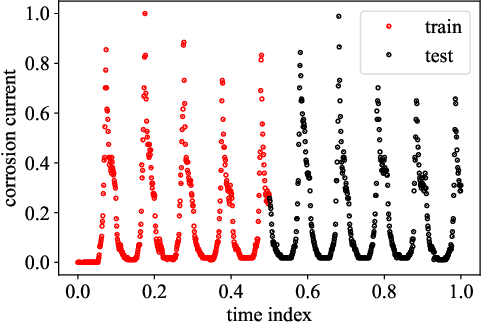
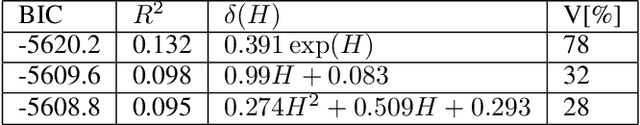
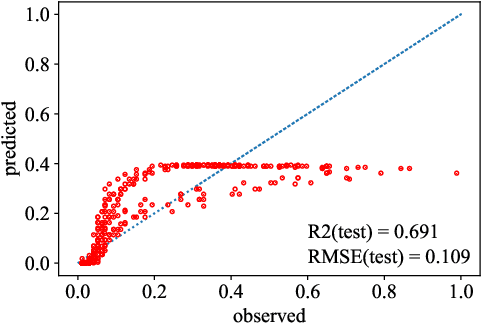
Most common mechanistic models are traditionally presented in mathematical forms to explain a given physical phenomenon. Machine learning algorithms, on the other hand, provide a mechanism to map the input data to output without explicitly describing the underlying physical process that generated the data. We propose a Data-based Physics Discovery (DPD) framework for automatic discovery of governing equations from observed data. Without a prior definition of the model structure, first a free-form of the equation is discovered, and then calibrated and validated against the available data. In addition to the observed data, the DPD framework can utilize available prior physical models, and domain expert feedback. When prior models are available, the DPD framework can discover an additive or multiplicative correction term represented symbolically. The correction term can be a function of the existing input variable to the prior model, or a newly introduced variable. In case a prior model is not available, the DPD framework discovers a new data-based standalone model governing the observations. We demonstrate the performance of the proposed framework on a real-world application in the aerospace industry.

Bayesian task embedding for few-shot Bayesian optimization

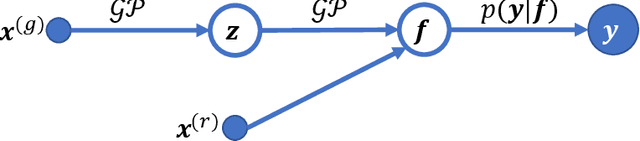
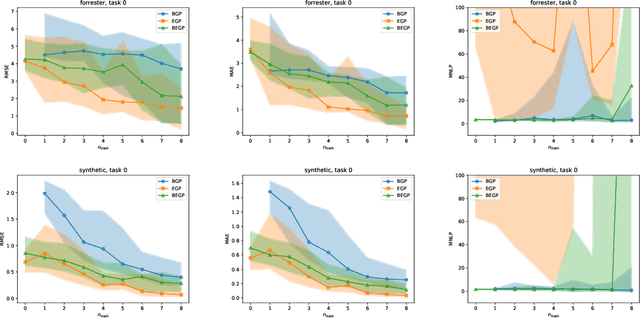
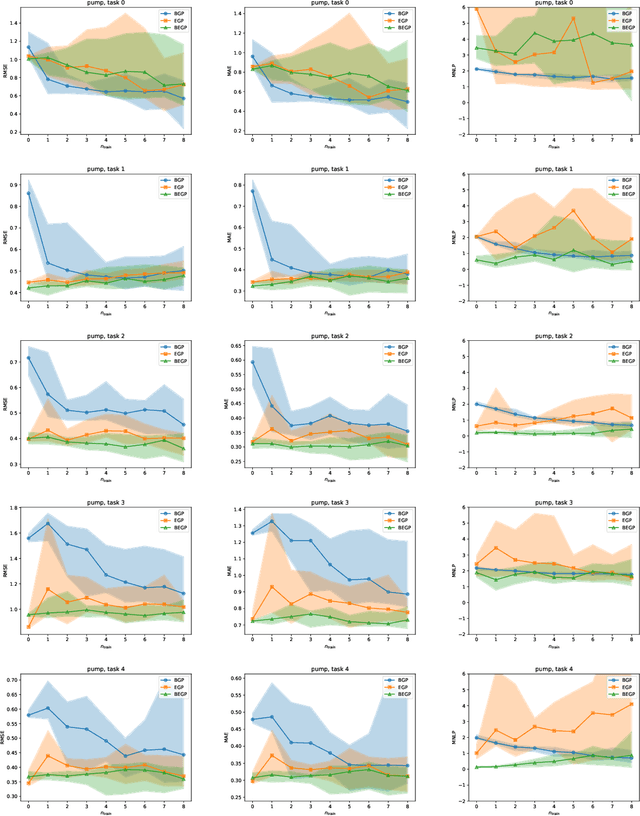
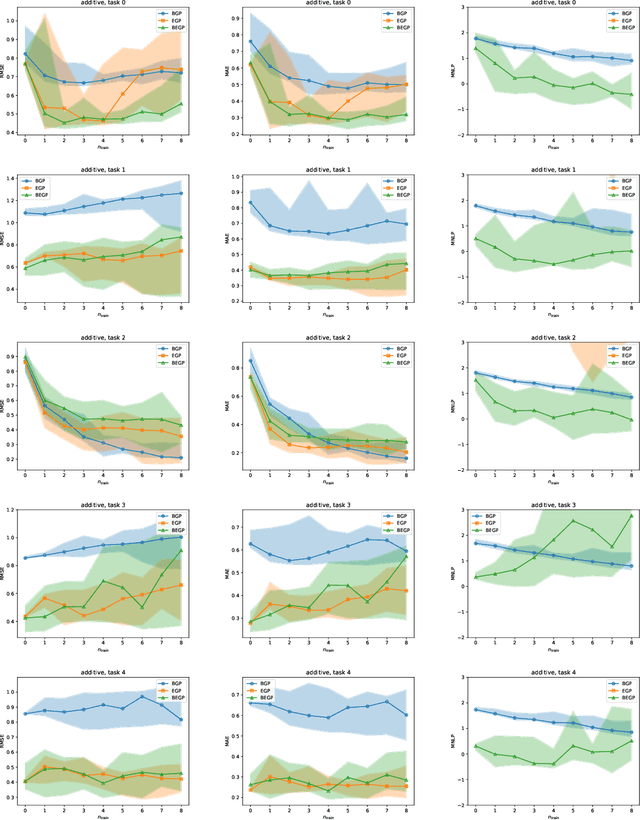
We describe a method for Bayesian optimization by which one may incorporate data from multiple systems whose quantitative interrelationships are unknown a priori. All general (nonreal-valued) features of the systems are associated with continuous latent variables that enter as inputs into a single metamodel that simultaneously learns the response surfaces of all of the systems. Bayesian inference is used to determine appropriate beliefs regarding the latent variables. We explain how the resulting probabilistic metamodel may be used for Bayesian optimization tasks and demonstrate its implementation on a variety of synthetic and real-world examples, comparing its performance under zero-, one-, and few-shot settings against traditional Bayesian optimization, which usually requires substantially more data from the system of interest.

Data-driven discovery of free-form governing differential equations

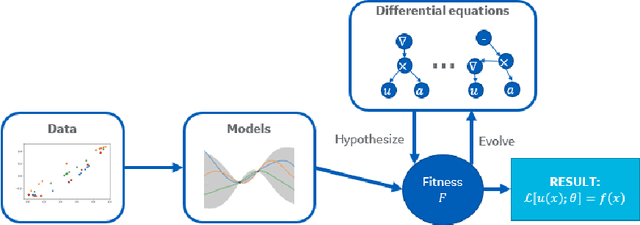
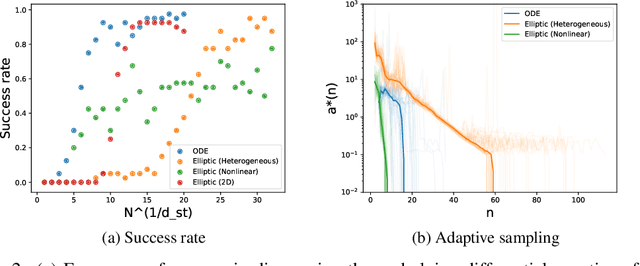
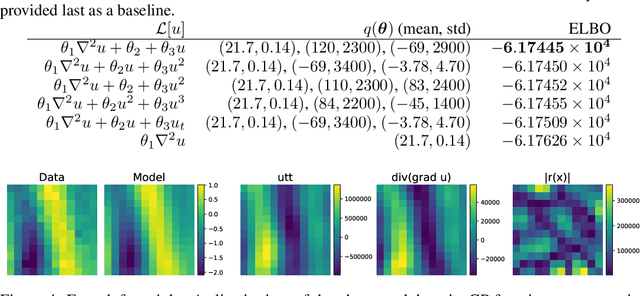
We present a method of discovering governing differential equations from data without the need to specify a priori the terms to appear in the equation. The input to our method is a dataset (or ensemble of datasets) corresponding to a particular solution (or ensemble of particular solutions) of a differential equation. The output is a human-readable differential equation with parameters calibrated to the individual particular solutions provided. The key to our method is to learn differentiable models of the data that subsequently serve as inputs to a genetic programming algorithm in which graphs specify computation over arbitrary compositions of functions, parameters, and (potentially differential) operators on functions. Differential operators are composed and evaluated using recursive application of automatic differentiation, allowing our algorithm to explore arbitrary compositions of operators without the need for human intervention. We also demonstrate an active learning process to identify and remedy deficiencies in the proposed governing equations.