Inverse Aerodynamic Design of Gas Turbine Blades using Probabilistic Machine Learning

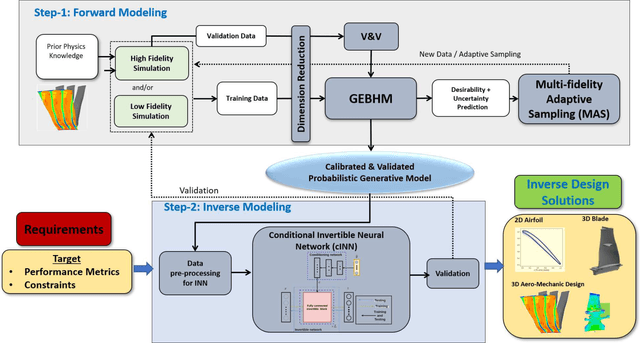
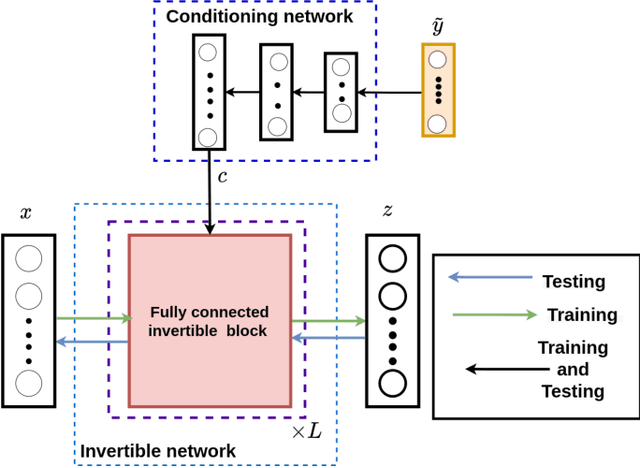
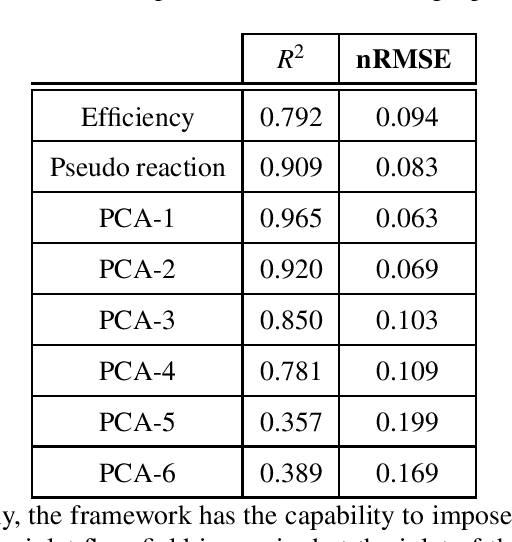
One of the critical components in Industrial Gas Turbines (IGT) is the turbine blade. Design of turbine blades needs to consider multiple aspects like aerodynamic efficiency, durability, safety and manufacturing, which make the design process sequential and iterative.The sequential nature of these iterations forces a long design cycle time, ranging from several months to years. Due to the reactionary nature of these iterations, little effort has been made to accumulate data in a manner that allows for deep exploration and understanding of the total design space. This is exemplified in the process of designing the individual components of the IGT resulting in a potential unrealized efficiency. To overcome the aforementioned challenges, we demonstrate a probabilistic inverse design machine learning framework (PMI), to carry out an explicit inverse design. PMI calculates the design explicitly without excessive costly iteration and overcomes the challenges associated with ill-posed inverse problems. In this work, the framework will be demonstrated on inverse aerodynamic design of three-dimensional turbine blades.

Discovery of Physics and Characterization of Microstructure from Data with Bayesian Hidden Physics Models

There has been a surge in the interest of using machine learning techniques to assist in the scientific process of formulating knowledge to explain observational data. We demonstrate the use of Bayesian Hidden Physics Models to first uncover the physics governing the propagation of acoustic impulses in metallic specimens using data obtained from a pristine sample. We then use the learned physics to characterize the microstructure of a separate specimen with a surface-breaking crack flaw. Remarkably, we find that the physics learned from the first specimen allows us to understand the backscattering observed in the latter sample, a qualitative feature that is wholly absent from the specimen from which the physics were inferred. The backscattering is explained through inhomogeneities of a latent spatial field that can be recognized as the speed of sound in the media.

Bayesian Hidden Physics Models: Uncertainty Quantification for Discovery of Nonlinear Partial Differential Operators from Data

What do data tell us about physics-and what don't they tell us? There has been a surge of interest in using machine learning models to discover governing physical laws such as differential equations from data, but current methods lack uncertainty quantification to communicate their credibility. This work addresses this shortcoming from a Bayesian perspective. We introduce a novel model comprising "leaf" modules that learn to represent distinct experiments' spatiotemporal functional data as neural networks and a single "root" module that expresses a nonparametric distribution over their governing nonlinear differential operator as a Gaussian process. Automatic differentiation is used to compute the required partial derivatives from the leaf functions as inputs to the root. Our approach quantifies the reliability of the learned physics in terms of a posterior distribution over operators and propagates this uncertainty to solutions of novel initial-boundary value problem instances. Numerical experiments demonstrate the method on several nonlinear PDEs.

Advances in Bayesian Probabilistic Modeling for Industrial Applications

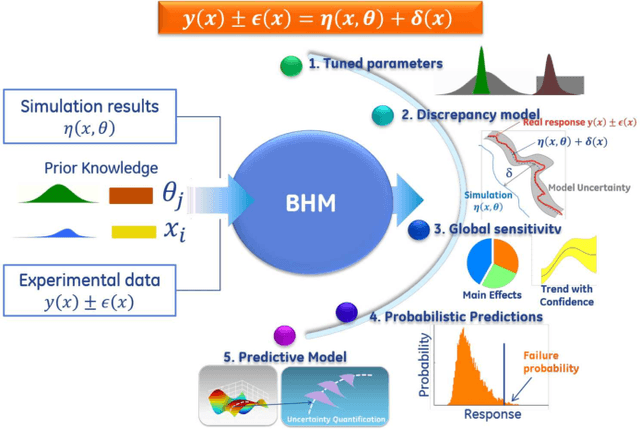
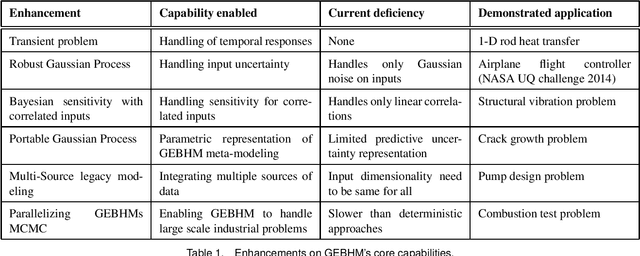
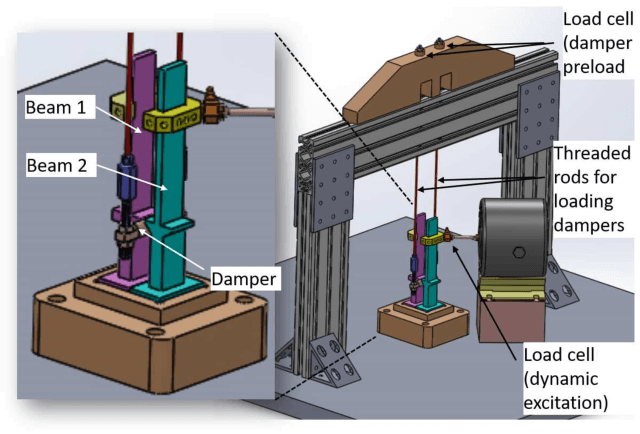
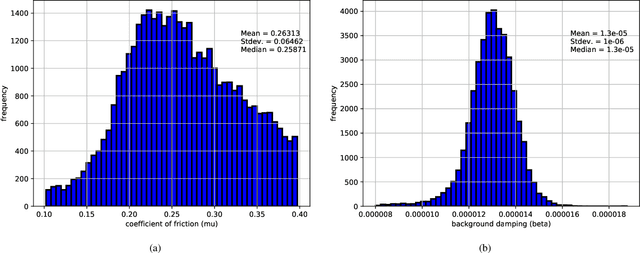
Industrial applications frequently pose a notorious challenge for state-of-the-art methods in the contexts of optimization, designing experiments and modeling unknown physical response. This problem is aggravated by limited availability of clean data, uncertainty in available physics-based models and additional logistic and computational expense associated with experiments. In such a scenario, Bayesian methods have played an impactful role in alleviating the aforementioned obstacles by quantifying uncertainty of different types under limited resources. These methods, usually deployed as a framework, allows decision makers to make informed choices under uncertainty while being able to incorporate information on the the fly, usually in the form of data, from multiple sources while being consistent with the physical intuition about the problem. This is a major advantage that Bayesian methods bring to fruition especially in the industrial context. This paper is a compendium of the Bayesian modeling methodology that is being consistently developed at GE Research. The methodology, called GE's Bayesian Hybrid Modeling (GEBHM), is a probabilistic modeling method, based on the Kennedy and O'Hagan framework, that has been continuously scaled-up and industrialized over several years. In this work, we explain the various advancements in GEBHM's methods and demonstrate their impact on several challenging industrial problems.

Bayesian task embedding for few-shot Bayesian optimization

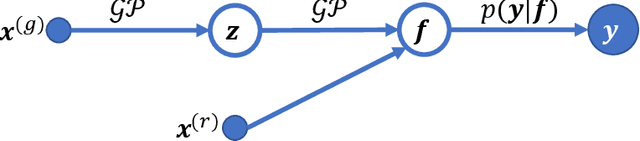
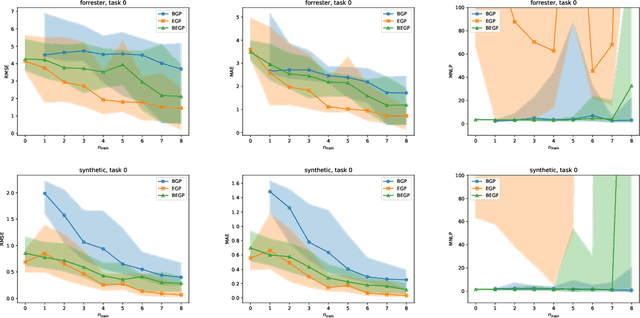
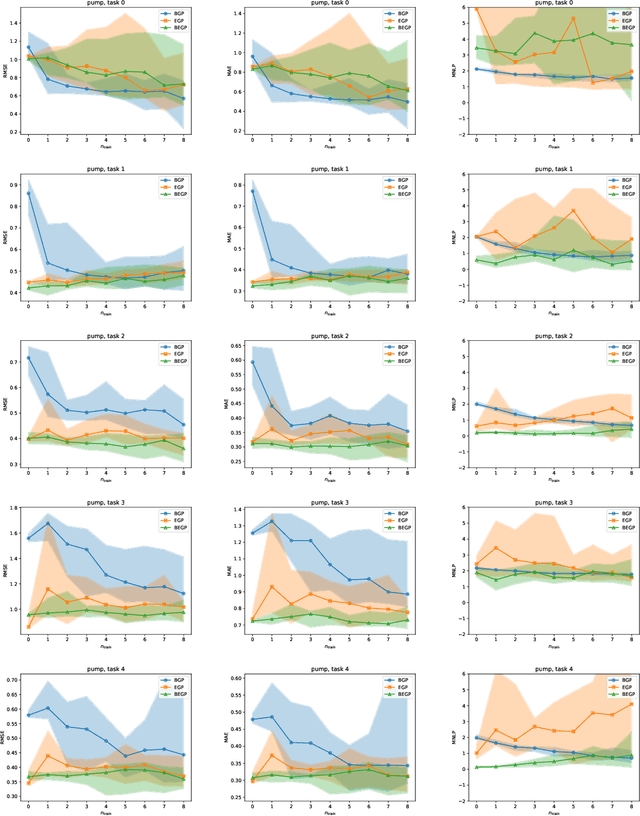
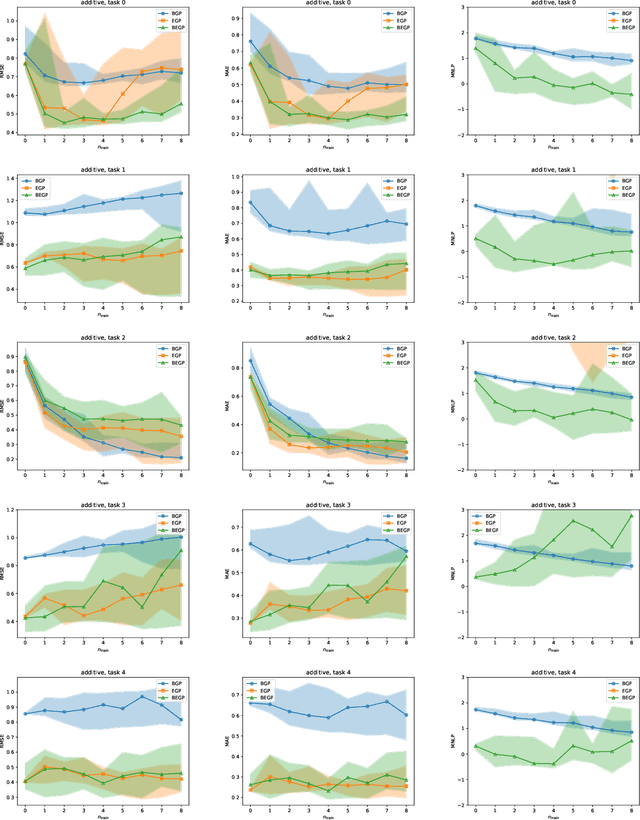
We describe a method for Bayesian optimization by which one may incorporate data from multiple systems whose quantitative interrelationships are unknown a priori. All general (nonreal-valued) features of the systems are associated with continuous latent variables that enter as inputs into a single metamodel that simultaneously learns the response surfaces of all of the systems. Bayesian inference is used to determine appropriate beliefs regarding the latent variables. We explain how the resulting probabilistic metamodel may be used for Bayesian optimization tasks and demonstrate its implementation on a variety of synthetic and real-world examples, comparing its performance under zero-, one-, and few-shot settings against traditional Bayesian optimization, which usually requires substantially more data from the system of interest.

Data-driven discovery of free-form governing differential equations

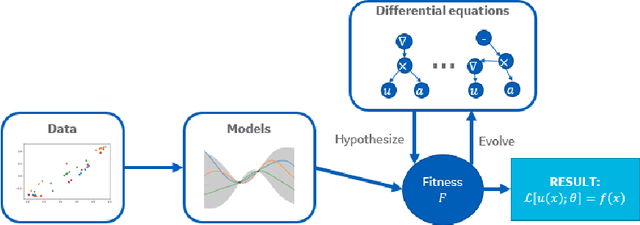
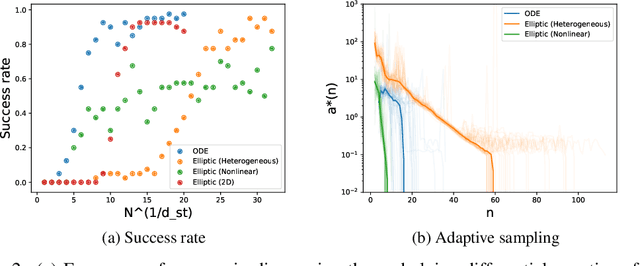
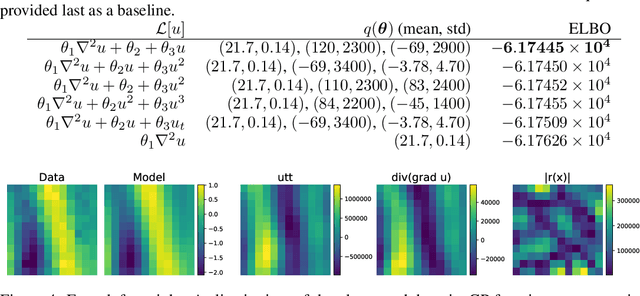
We present a method of discovering governing differential equations from data without the need to specify a priori the terms to appear in the equation. The input to our method is a dataset (or ensemble of datasets) corresponding to a particular solution (or ensemble of particular solutions) of a differential equation. The output is a human-readable differential equation with parameters calibrated to the individual particular solutions provided. The key to our method is to learn differentiable models of the data that subsequently serve as inputs to a genetic programming algorithm in which graphs specify computation over arbitrary compositions of functions, parameters, and (potentially differential) operators on functions. Differential operators are composed and evaluated using recursive application of automatic differentiation, allowing our algorithm to explore arbitrary compositions of operators without the need for human intervention. We also demonstrate an active learning process to identify and remedy deficiencies in the proposed governing equations.

Structured Bayesian Gaussian process latent variable model: applications to data-driven dimensionality reduction and high-dimensional inversion

We introduce a methodology for nonlinear inverse problems using a variational Bayesian approach where the unknown quantity is a spatial field. A structured Bayesian Gaussian process latent variable model is used both to construct a low-dimensional generative model of the sample-based stochastic prior as well as a surrogate for the forward evaluation. Its Bayesian formulation captures epistemic uncertainty introduced by the limited number of input and output examples, automatically selects an appropriate dimensionality for the learned latent representation of the data, and rigorously propagates the uncertainty of the data-driven dimensionality reduction of the stochastic space through the forward model surrogate. The structured Gaussian process model explicitly leverages spatial information for an informative generative prior to improve sample efficiency while achieving computational tractability through Kronecker product decompositions of the relevant kernel matrices. Importantly, the Bayesian inversion is carried out by solving a variational optimization problem, replacing traditional computationally-expensive Monte Carlo sampling. The methodology is demonstrated on an elliptic PDE and is shown to return well-calibrated posteriors and is tractable with latent spaces with over 100 dimensions.

Structured Bayesian Gaussian process latent variable model

We introduce a Bayesian Gaussian process latent variable model that explicitly captures spatial correlations in data using a parameterized spatial kernel and leveraging structure-exploiting algebra on the model covariance matrices for computational tractability. Inference is made tractable through a collapsed variational bound with similar computational complexity to that of the traditional Bayesian GP-LVM. Inference over partially-observed test cases is achieved by optimizing a "partially-collapsed" bound. Modeling high-dimensional time series systems is enabled through use of a dynamical GP latent variable prior. Examples imputing missing data on images and super-resolution imputation of missing video frames demonstrate the model.