Heterogenous Multi-Source Data Fusion Through Input Mapping and Latent Variable Gaussian Process

Artificial intelligence and machine learning frameworks have served as computationally efficient mapping between inputs and outputs for engineering problems. These mappings have enabled optimization and analysis routines that have warranted superior designs, ingenious material systems and optimized manufacturing processes. A common occurrence in such modeling endeavors is the existence of multiple source of data, each differentiated by fidelity, operating conditions, experimental conditions, and more. Data fusion frameworks have opened the possibility of combining such differentiated sources into single unified models, enabling improved accuracy and knowledge transfer. However, these frameworks encounter limitations when the different sources are heterogeneous in nature, i.e., not sharing the same input parameter space. These heterogeneous input scenarios can occur when the domains differentiated by complexity, scale, and fidelity require different parametrizations. Towards addressing this void, a heterogeneous multi-source data fusion framework is proposed based on input mapping calibration (IMC) and latent variable Gaussian process (LVGP). In the first stage, the IMC algorithm is utilized to transform the heterogeneous input parameter spaces into a unified reference parameter space. In the second stage, a multi-source data fusion model enabled by LVGP is leveraged to build a single source-aware surrogate model on the transformed reference space. The proposed framework is demonstrated and analyzed on three engineering case studies (design of cantilever beam, design of ellipsoidal void and modeling properties of Ti6Al4V alloy). The results indicate that the proposed framework provides improved predictive accuracy over a single source model and transformed but source unaware model.

Interpretable Multi-Source Data Fusion Through Latent Variable Gaussian Process

With the advent of artificial intelligence (AI) and machine learning (ML), various domains of science and engineering communites has leveraged data-driven surrogates to model complex systems from numerous sources of information (data). The proliferation has led to significant reduction in cost and time involved in development of superior systems designed to perform specific functionalities. A high proposition of such surrogates are built extensively fusing multiple sources of data, may it be published papers, patents, open repositories, or other resources. However, not much attention has been paid to the differences in quality and comprehensiveness of the known and unknown underlying physical parameters of the information sources that could have downstream implications during system optimization. Towards resolving this issue, a multi-source data fusion framework based on Latent Variable Gaussian Process (LVGP) is proposed. The individual data sources are tagged as a characteristic categorical variable that are mapped into a physically interpretable latent space, allowing the development of source-aware data fusion modeling. Additionally, a dissimilarity metric based on the latent variables of LVGP is introduced to study and understand the differences in the sources of data. The proposed approach is demonstrated on and analyzed through two mathematical (representative parabola problem, 2D Ackley function) and two materials science (design of FeCrAl and SmCoFe alloys) case studies. From the case studies, it is observed that compared to using single-source and source unaware ML models, the proposed multi-source data fusion framework can provide better predictions for sparse-data problems, interpretability regarding the sources, and enhanced modeling capabilities by taking advantage of the correlations and relationships among different sources.

Mixed-Variable Global Sensitivity Analysis For Knowledge Discovery And Efficient Combinatorial Materials Design

Global Sensitivity Analysis (GSA) is the study of the influence of any given inputs on the outputs of a model. In the context of engineering design, GSA has been widely used to understand both individual and collective contributions of design variables on the design objectives. So far, global sensitivity studies have often been limited to design spaces with only quantitative (numerical) design variables. However, many engineering systems also contain, if not only, qualitative (categorical) design variables in addition to quantitative design variables. In this paper, we integrate Latent Variable Gaussian Process (LVGP) with Sobol' analysis to develop the first metamodel-based mixed-variable GSA method. Through numerical case studies, we validate and demonstrate the effectiveness of our proposed method for mixed-variable problems. Furthermore, while the proposed GSA method is general enough to benefit various engineering design applications, we integrate it with multi-objective Bayesian optimization (BO) to create a sensitivity-aware design framework in accelerating the Pareto front design exploration for metal-organic framework (MOF) materials with many-level combinatorial design spaces. Although MOFs are constructed only from qualitative variables that are notoriously difficult to design, our method can utilize sensitivity analysis to navigate the optimization in the many-level large combinatorial design space, greatly expediting the exploration of novel MOF candidates.

A Latent Variable Approach for Non-Hierarchical Multi-Fidelity Adaptive Sampling

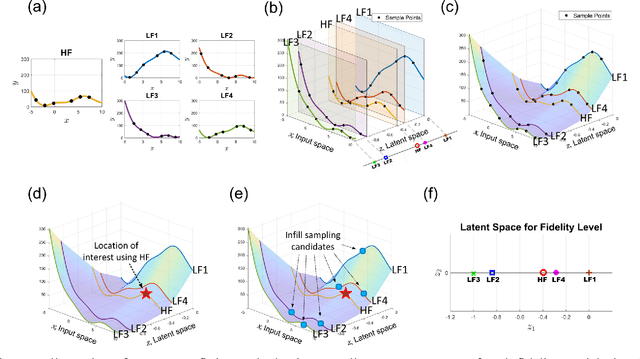
Multi-fidelity (MF) methods are gaining popularity for enhancing surrogate modeling and design optimization by incorporating data from various low-fidelity (LF) models. While most existing MF methods assume a fixed dataset, adaptive sampling methods that dynamically allocate resources among fidelity models can achieve higher efficiency in the exploring and exploiting the design space. However, most existing MF methods rely on the hierarchical assumption of fidelity levels or fail to capture the intercorrelation between multiple fidelity levels and utilize it to quantify the value of the future samples and navigate the adaptive sampling. To address this hurdle, we propose a framework hinged on a latent embedding for different fidelity models and the associated pre-posterior analysis to explicitly utilize their correlation for adaptive sampling. In this framework, each infill sampling iteration includes two steps: We first identify the location of interest with the greatest potential improvement using the high-fidelity (HF) model, then we search for the next sample across all fidelity levels that maximize the improvement per unit cost at the location identified in the first step. This is made possible by a single Latent Variable Gaussian Process (LVGP) model that maps different fidelity models into an interpretable latent space to capture their correlations without assuming hierarchical fidelity levels. The LVGP enables us to assess how LF sampling candidates will affect HF response with pre-posterior analysis and determine the next sample with the best benefit-to-cost ratio. Through test cases, we demonstrate that the proposed method outperforms the benchmark methods in both MF global fitting (GF) and Bayesian Optimization (BO) problems in convergence rate and robustness. Moreover, the method offers the flexibility to switch between GF and BO by simply changing the acquisition function.

Rapid Design of Top-Performing Metal-Organic Frameworks with Qualitative Representations of Building Blocks

Data-driven materials design often encounters challenges where systems require or possess qualitative (categorical) information. Metal-organic frameworks (MOFs) are an example of such material systems. The representation of MOFs through different building blocks makes it a challenge for designers to incorporate qualitative information into design optimization. Furthermore, the large number of potential building blocks leads to a combinatorial challenge, with millions of possible MOFs that could be explored through time consuming physics-based approaches. In this work, we integrated Latent Variable Gaussian Process (LVGP) and Multi-Objective Batch-Bayesian Optimization (MOBBO) to identify top-performing MOFs adaptively, autonomously, and efficiently without any human intervention. Our approach provides three main advantages: (i) no specific physical descriptors are required and only building blocks that construct the MOFs are used in global optimization through qualitative representations, (ii) the method is application and property independent, and (iii) the latent variable approach provides an interpretable model of qualitative building blocks with physical justification. To demonstrate the effectiveness of our method, we considered a design space with more than 47,000 MOF candidates. By searching only ~1% of the design space, LVGP-MOBBO was able to identify all MOFs on the Pareto front and more than 97% of the 50 top-performing designs for the CO$_2$ working capacity and CO$_2$/N$_2$ selectivity properties. Finally, we compared our approach with the Random Forest algorithm and demonstrated its efficiency, interpretability, and robustness.