Adaptive Digital Twin of Sheet Metal Forming via Proper Orthogonal Decomposition-Based Koopman Operator with Model Predictive Control

Digital Twin (DT) technologies are transforming manufacturing by enabling real-time prediction, monitoring, and control of complex processes. Yet, applying DT to deformation-based metal forming remains challenging because of the strongly coupled spatial-temporal behavior and the nonlinear relationship between toolpath and material response. For instance, sheet-metal forming by the English wheel, a highly flexible but artisan-dependent process, still lacks digital counterparts that can autonomously plan and adapt forming strategies. This study presents an adaptive DT framework that integrates Proper Orthogonal Decomposition (POD) for physics-aware dimensionality reduction with a Koopman operator for representing nonlinear system in a linear lifted space for the real-time decision-making via model predictive control (MPC). To accommodate evolving process conditions or material states, an online Recursive Least Squares (RLS) algorithm is introduced to update the operator coefficients in real time, enabling continuous adaptation of the DT model as new deformation data become available. The proposed framework is experimentally demonstrated on a robotic English Wheel sheet metal forming system, where deformation fields are measured and modeled under varying toolpaths. Results show that the adaptive DT is capable of controlling the forming process to achieve the given target shape by effectively capturing non-stationary process behaviors. Beyond this case study, the proposed framework establishes a generalizable approach for interpretable, adaptive, and computationally-efficient DT of nonlinear manufacturing systems, bridging reduced-order physics representations with data-driven adaptability to support autonomous process control and optimization.

An Attention-based Spatio-Temporal Neural Operator for Evolving Physics

In scientific machine learning (SciML), a key challenge is learning unknown, evolving physical processes and making predictions across spatio-temporal scales. For example, in real-world manufacturing problems like additive manufacturing, users adjust known machine settings while unknown environmental parameters simultaneously fluctuate. To make reliable predictions, it is desired for a model to not only capture long-range spatio-temporal interactions from data but also adapt to new and unknown environments; traditional machine learning models excel at the first task but often lack physical interpretability and struggle to generalize under varying environmental conditions. To tackle these challenges, we propose the Attention-based Spatio-Temporal Neural Operator (ASNO), a novel architecture that combines separable attention mechanisms for spatial and temporal interactions and adapts to unseen physical parameters. Inspired by the backward differentiation formula (BDF), ASNO learns a transformer for temporal prediction and extrapolation and an attention-based neural operator for handling varying external loads, enhancing interpretability by isolating historical state contributions and external forces, enabling the discovery of underlying physical laws and generalizability to unseen physical environments. Empirical results on SciML benchmarks demonstrate that ASNO outperforms over existing models, establishing its potential for engineering applications, physics discovery, and interpretable machine learning.

Real-Time Decision-Making for Digital Twin in Additive Manufacturing with Model Predictive Control using Time-Series Deep Neural Networks

Digital Twin-a virtual replica of a physical system enabling real-time monitoring, model updating, prediction, and decision-making-combined with recent advances in machine learning (ML), offers new opportunities for proactive control strategies in autonomous manufacturing. However, achieving real-time decision-making with Digital Twins requires efficient optimization driven by accurate predictions of highly nonlinear manufacturing systems. This paper presents a simultaneous multi-step Model Predictive Control (MPC) framework for real-time decision-making, using a multi-variate deep neural network (DNN), named Time-Series Dense Encoder (TiDE), as the surrogate model. Different from the models in conventional MPC which only provide one-step ahead prediction, TiDE is capable of predicting future states within the prediction horizon in one shot (multi-step), significantly accelerating MPC. Using Directed Energy Deposition additive manufacturing as a case study, we demonstrate the effectiveness of the proposed MPC in achieving melt pool temperature tracking to ensure part quality, while reducing porosity defects by regulating laser power to maintain melt pool depth constraints. In this work, we first show that TiDE is capable of accurately predicting melt pool temperature and depth. Second, we demonstrate that the proposed MPC achieves precise temperature tracking while satisfying melt pool depth constraints within a targeted dilution range (10%-30%), reducing potential porosity defects. Compared to the PID controller, MPC results in smoother and less fluctuating laser power profiles with competitive or superior melt pool temperature control performance. This demonstrates MPC's proactive control capabilities, leveraging time-series prediction and real-time optimization, positioning it as a powerful tool for future Digital Twin applications and real-time process optimization in manufacturing.

A Latent Variable Approach for Non-Hierarchical Multi-Fidelity Adaptive Sampling

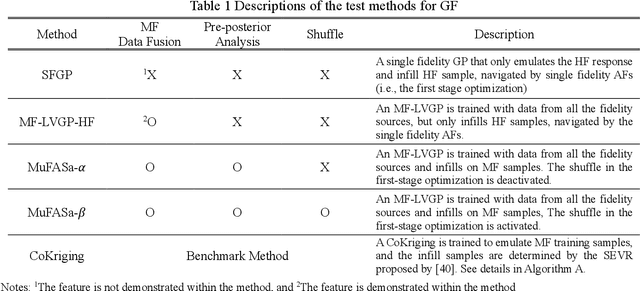
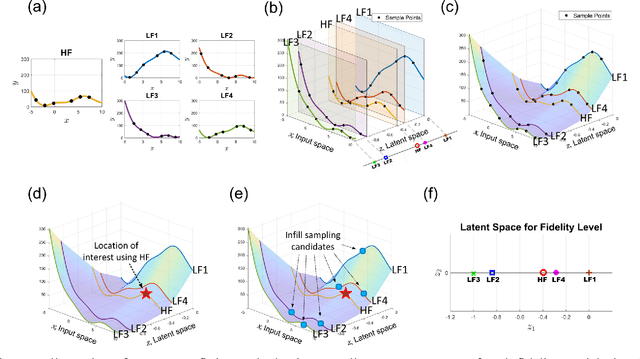
Multi-fidelity (MF) methods are gaining popularity for enhancing surrogate modeling and design optimization by incorporating data from various low-fidelity (LF) models. While most existing MF methods assume a fixed dataset, adaptive sampling methods that dynamically allocate resources among fidelity models can achieve higher efficiency in the exploring and exploiting the design space. However, most existing MF methods rely on the hierarchical assumption of fidelity levels or fail to capture the intercorrelation between multiple fidelity levels and utilize it to quantify the value of the future samples and navigate the adaptive sampling. To address this hurdle, we propose a framework hinged on a latent embedding for different fidelity models and the associated pre-posterior analysis to explicitly utilize their correlation for adaptive sampling. In this framework, each infill sampling iteration includes two steps: We first identify the location of interest with the greatest potential improvement using the high-fidelity (HF) model, then we search for the next sample across all fidelity levels that maximize the improvement per unit cost at the location identified in the first step. This is made possible by a single Latent Variable Gaussian Process (LVGP) model that maps different fidelity models into an interpretable latent space to capture their correlations without assuming hierarchical fidelity levels. The LVGP enables us to assess how LF sampling candidates will affect HF response with pre-posterior analysis and determine the next sample with the best benefit-to-cost ratio. Through test cases, we demonstrate that the proposed method outperforms the benchmark methods in both MF global fitting (GF) and Bayesian Optimization (BO) problems in convergence rate and robustness. Moreover, the method offers the flexibility to switch between GF and BO by simply changing the acquisition function.