Application of probabilistic modeling and automated machine learning framework for high-dimensional stress field

Modern computational methods, involving highly sophisticated mathematical formulations, enable several tasks like modeling complex physical phenomenon, predicting key properties and design optimization. The higher fidelity in these computer models makes it computationally intensive to query them hundreds of times for optimization and one usually relies on a simplified model albeit at the cost of losing predictive accuracy and precision. Towards this, data-driven surrogate modeling methods have shown a lot of promise in emulating the behavior of the expensive computer models. However, a major bottleneck in such methods is the inability to deal with high input dimensionality and the need for relatively large datasets. With such problems, the input and output quantity of interest are tensors of high dimensionality. Commonly used surrogate modeling methods for such problems, suffer from requirements like high number of computational evaluations that precludes one from performing other numerical tasks like uncertainty quantification and statistical analysis. In this work, we propose an end-to-end approach that maps a high-dimensional image like input to an output of high dimensionality or its key statistics. Our approach uses two main framework that perform three steps: a) reduce the input and output from a high-dimensional space to a reduced or low-dimensional space, b) model the input-output relationship in the low-dimensional space, and c) enable the incorporation of domain-specific physical constraints as masks. In order to accomplish the task of reducing input dimensionality we leverage principal component analysis, that is coupled with two surrogate modeling methods namely: a) Bayesian hybrid modeling, and b) DeepHyper's deep neural networks. We demonstrate the applicability of the approach on a problem of a linear elastic stress field data.

Stress field prediction in fiber-reinforced composite materials using a deep learning approach

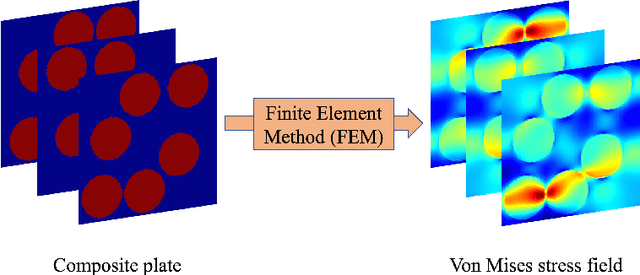
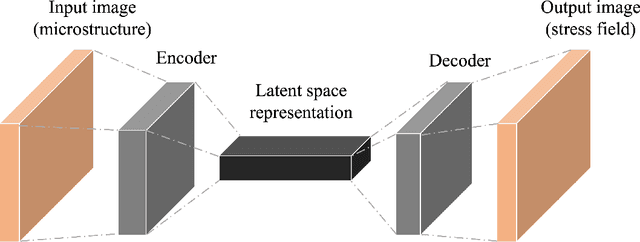
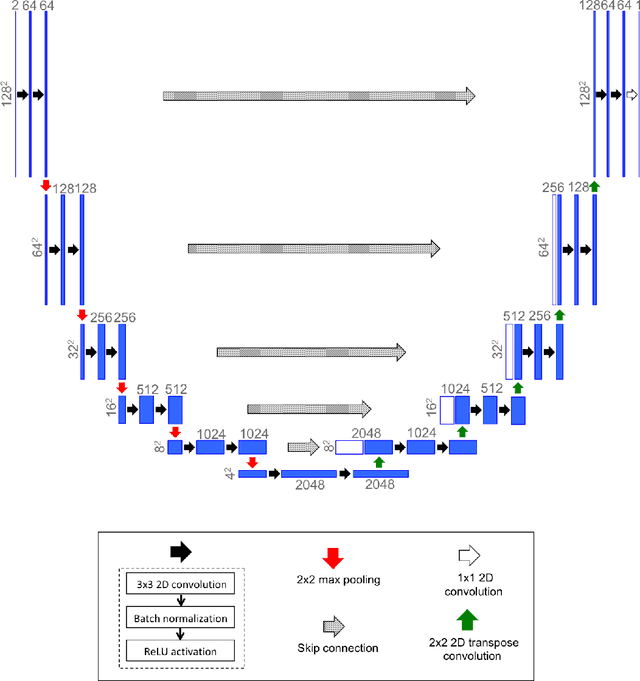
Computational stress analysis is an important step in the design of material systems. Finite element method (FEM) is a standard approach of performing stress analysis of complex material systems. A way to accelerate stress analysis is to replace FEM with a data-driven machine learning based stress analysis approach. In this study, we consider a fiber-reinforced matrix composite material system and we use deep learning tools to find an alternative to the FEM approach for stress field prediction. We first try to predict stress field maps for composite material systems of fixed number of fibers with varying spatial configurations. Specifically, we try to find a mapping between the spatial arrangement of the fibers in the composite material and the corresponding von Mises stress field. This is achieved by using a convolutional neural network (CNN), specifically a U-Net architecture, using true stress maps of systems with same number of fibers as training data. U-Net is a encoder-decoder network which in this study takes in the composite material image as an input and outputs the stress field image which is of the same size as the input image. We perform a robustness analysis by taking different initializations of the training samples to find the sensitivity of the prediction accuracy to the small number of training samples. When the number of fibers in the composite material system is increased for the same volume fraction, a finer finite element mesh discretization is required to represent the geometry accurately. This leads to an increase in the computational cost. Thus, the secondary goal here is to predict the stress field for systems with larger number of fibers with varying spatial configurations using information from the true stress maps of relatively cheaper systems of smaller fiber number.

An efficient optimization based microstructure reconstruction approach with multiple loss functions

Stochastic microstructure reconstruction involves digital generation of microstructures that match key statistics and characteristics of a (set of) target microstructure(s). This process enables computational analyses on ensembles of microstructures without having to perform exhaustive and costly experimental characterizations. Statistical functions-based and deep learning-based methods are among the stochastic microstructure reconstruction approaches applicable to a wide range of material systems. In this paper, we integrate statistical descriptors as well as feature maps from a pre-trained deep neural network into an overall loss function for an optimization based reconstruction procedure. This helps us to achieve significant computational efficiency in reconstructing microstructures that retain the critically important physical properties of the target microstructure. A numerical example for the microstructure reconstruction of bi-phase random porous ceramic material demonstrates the efficiency of the proposed methodology. We further perform a detailed finite element analysis (FEA) of the reconstructed microstructures to calculate effective elastic modulus, effective thermal conductivity and effective hydraulic conductivity, in order to analyse the algorithm's capacity to capture the variability of these material properties with respect to those of the target microstructure. This method provides an economic, efficient and easy-to-use approach for reconstructing random multiphase materials in 2D which has the potential to be extended to 3D structures.

Probabilistic modeling of discrete structural response with application to composite plate penetration models

Discrete response of structures is often a key probabilistic quantity of interest. For example, one may need to identify the probability of a binary event, such as, whether a structure has buckled or not. In this study, an adaptive domain-based decomposition and classification method, combined with sparse grid sampling, is used to develop an efficient classification surrogate modeling algorithm for such discrete outputs. An assumption of monotonic behaviour of the output with respect to all model parameters, based on the physics of the problem, helps to reduce the number of model evaluations and makes the algorithm more efficient. As an application problem, this paper deals with the development of a computational framework for generation of probabilistic penetration response of S-2 glass/SC-15 epoxy composite plates under ballistic impact. This enables the computationally feasible generation of the probabilistic velocity response (PVR) curve or the $V_0-V_{100}$ curve as a function of the impact velocity, and the ballistic limit velocity prediction as a function of the model parameters. The PVR curve incorporates the variability of the model input parameters and describes the probability of penetration of the plate as a function of impact velocity.