Stress field prediction in fiber-reinforced composite materials using a deep learning approach

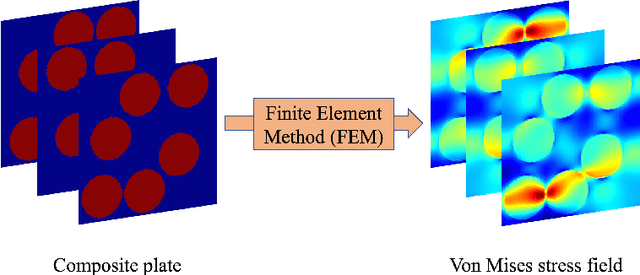
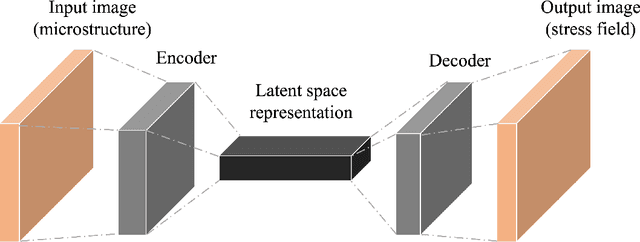
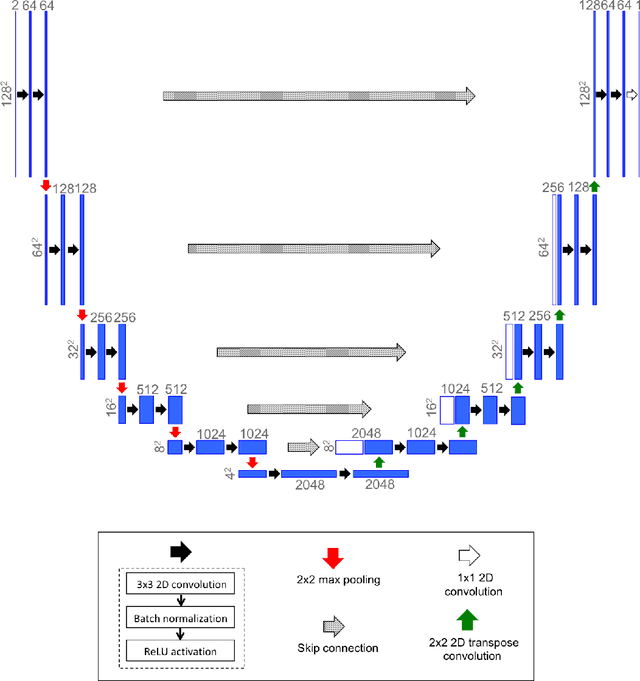
Computational stress analysis is an important step in the design of material systems. Finite element method (FEM) is a standard approach of performing stress analysis of complex material systems. A way to accelerate stress analysis is to replace FEM with a data-driven machine learning based stress analysis approach. In this study, we consider a fiber-reinforced matrix composite material system and we use deep learning tools to find an alternative to the FEM approach for stress field prediction. We first try to predict stress field maps for composite material systems of fixed number of fibers with varying spatial configurations. Specifically, we try to find a mapping between the spatial arrangement of the fibers in the composite material and the corresponding von Mises stress field. This is achieved by using a convolutional neural network (CNN), specifically a U-Net architecture, using true stress maps of systems with same number of fibers as training data. U-Net is a encoder-decoder network which in this study takes in the composite material image as an input and outputs the stress field image which is of the same size as the input image. We perform a robustness analysis by taking different initializations of the training samples to find the sensitivity of the prediction accuracy to the small number of training samples. When the number of fibers in the composite material system is increased for the same volume fraction, a finer finite element mesh discretization is required to represent the geometry accurately. This leads to an increase in the computational cost. Thus, the secondary goal here is to predict the stress field for systems with larger number of fibers with varying spatial configurations using information from the true stress maps of relatively cheaper systems of smaller fiber number.

An efficient optimization based microstructure reconstruction approach with multiple loss functions

Stochastic microstructure reconstruction involves digital generation of microstructures that match key statistics and characteristics of a (set of) target microstructure(s). This process enables computational analyses on ensembles of microstructures without having to perform exhaustive and costly experimental characterizations. Statistical functions-based and deep learning-based methods are among the stochastic microstructure reconstruction approaches applicable to a wide range of material systems. In this paper, we integrate statistical descriptors as well as feature maps from a pre-trained deep neural network into an overall loss function for an optimization based reconstruction procedure. This helps us to achieve significant computational efficiency in reconstructing microstructures that retain the critically important physical properties of the target microstructure. A numerical example for the microstructure reconstruction of bi-phase random porous ceramic material demonstrates the efficiency of the proposed methodology. We further perform a detailed finite element analysis (FEA) of the reconstructed microstructures to calculate effective elastic modulus, effective thermal conductivity and effective hydraulic conductivity, in order to analyse the algorithm's capacity to capture the variability of these material properties with respect to those of the target microstructure. This method provides an economic, efficient and easy-to-use approach for reconstructing random multiphase materials in 2D which has the potential to be extended to 3D structures.