Manifold Alignment-Based Multi-Fidelity Reduced-Order Modeling Applied to Structural Analysis

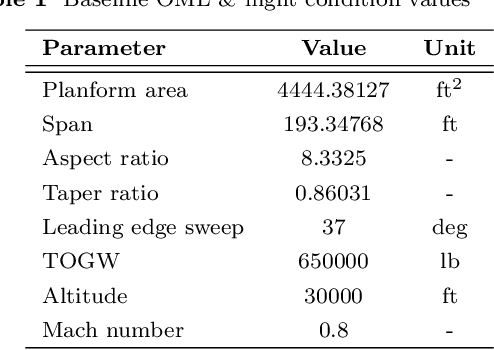
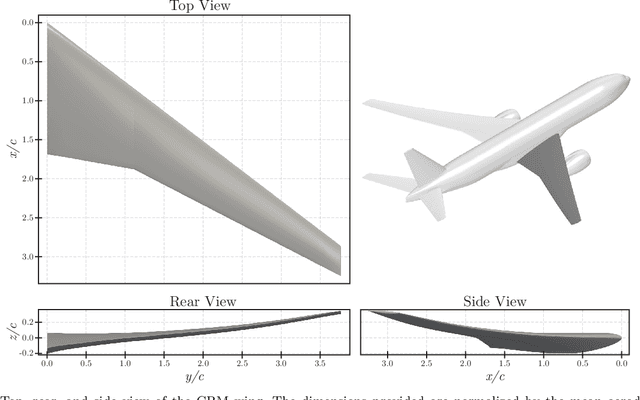
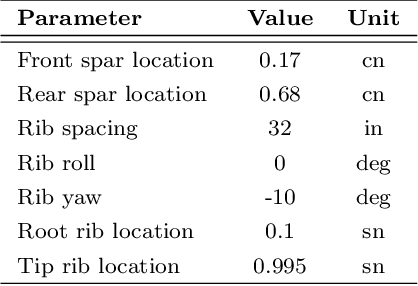
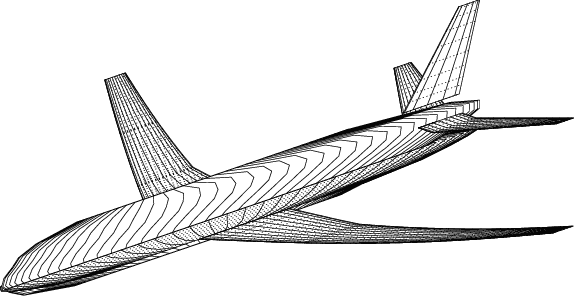
This work presents the application of a recently developed parametric, non-intrusive, and multi-fidelity reduced-order modeling method on high-dimensional displacement and stress fields arising from the structural analysis of geometries that differ in the size of discretization and structural topology.The proposed approach leverages manifold alignment to fuse inconsistent field outputs from high- and low-fidelity simulations by individually projecting their solution onto a common subspace. The effectiveness of the method is demonstrated on two multi-fidelity scenarios involving the structural analysis of a benchmark wing geometry. Results show that outputs from structural simulations using incompatible grids, or related yet different topologies, are easily combined into a single predictive model, thus eliminating the need for additional pre-processing of the data. The new multi-fidelity reduced-order model achieves a relatively higher predictive accuracy at a lower computational cost when compared to a single-fidelity model.

A Fully Bayesian Gradient-Free Supervised Dimension Reduction Method using Gaussian Processes

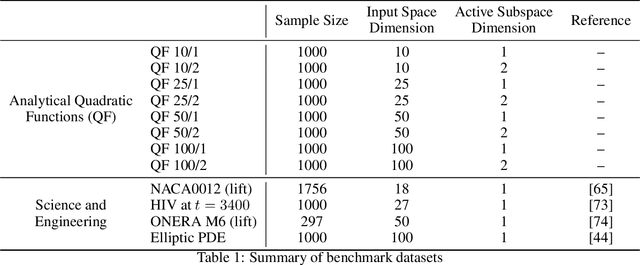
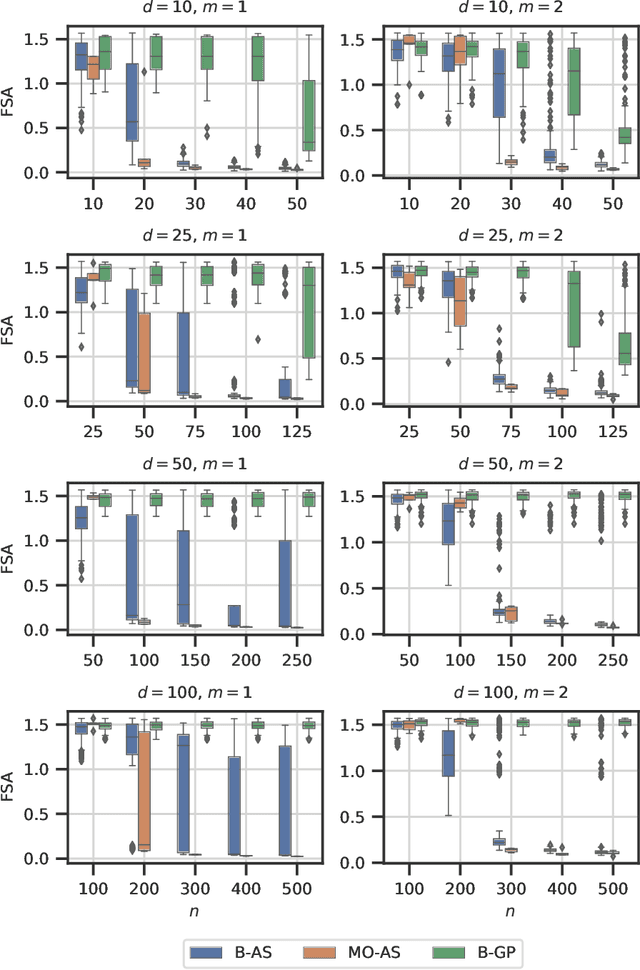
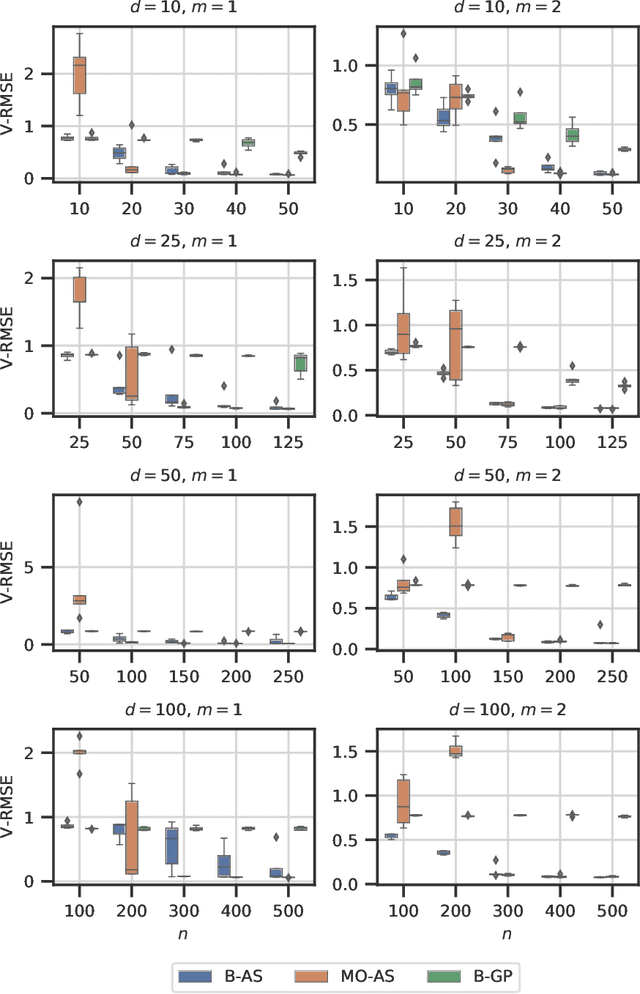
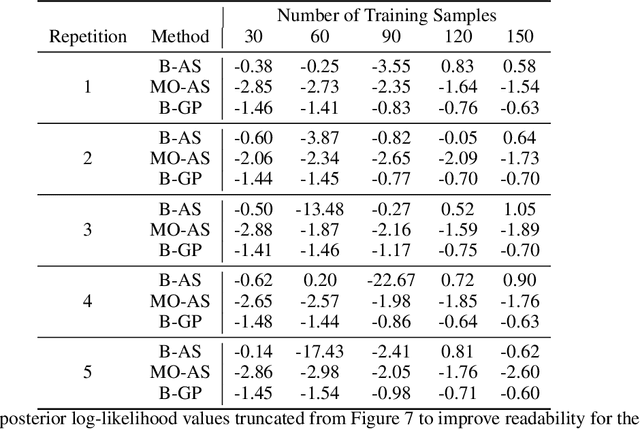
Modern day engineering problems are ubiquitously characterized by sophisticated computer codes that map parameters or inputs to an underlying physical process. In other situations, experimental setups are used to model the physical process in a laboratory, ensuring high precision while being costly in materials and logistics. In both scenarios, only limited amount of data can be generated by querying the expensive information source at a finite number of inputs or designs. This problem is compounded further in the presence of a high-dimensional input space. State-of-the-art parameter space dimension reduction methods, such as active subspace, aim to identify a subspace of the original input space that is sufficient to explain the output response. These methods are restricted by their reliance on gradient evaluations or copious data, making them inadequate to expensive problems without direct access to gradients. The proposed methodology is gradient-free and fully Bayesian, as it quantifies uncertainty in both the low-dimensional subspace and the surrogate model parameters. This enables a full quantification of epistemic uncertainty and robustness to limited data availability. It is validated on multiple datasets from engineering and science and compared to two other state-of-the-art methods based on four aspects: a) recovery of the active subspace, b) deterministic prediction accuracy, c) probabilistic prediction accuracy, and d) training time. The comparison shows that the proposed method improves the active subspace recovery and predictive accuracy, in both the deterministic and probabilistic sense, when only few model observations are available for training, at the cost of increased training time.

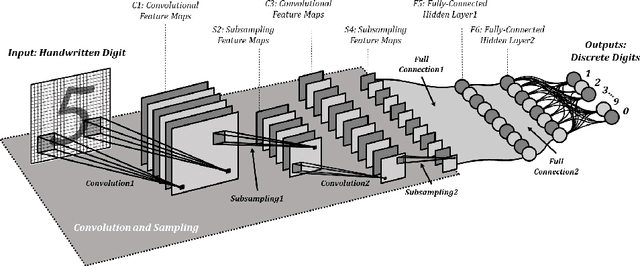
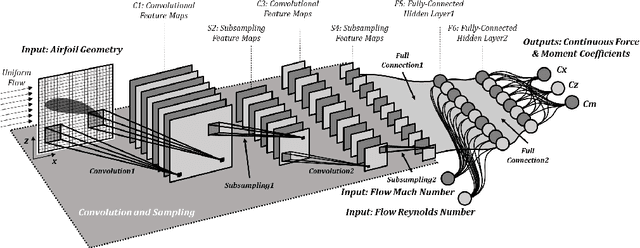
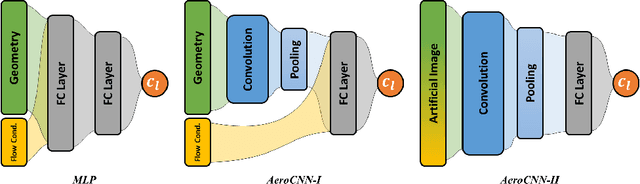
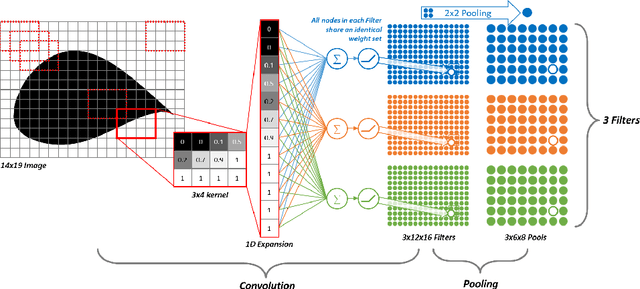
Application of Convolutional Neural Network to Predict Airfoil Lift Coefficient

The adaptability of the convolutional neural network (CNN) technique for aerodynamic meta-modeling tasks is probed in this work. The primary objective is to develop suitable CNN architecture for variable flow conditions and object geometry, in addition to identifying a sufficient data preparation process. Multiple CNN structures were trained to learn the lift coefficients of the airfoils with a variety of shapes in multiple flow Mach numbers, Reynolds numbers, and diverse angles of attack. This is conducted to illustrate the concept of the technique. A multi-layered perceptron (MLP) is also used for the training sets. The MLP results are compared with that of the CNN results. The newly proposed meta-modeling concept has been found to be comparable with the MLP in learning capability; and more importantly, our CNN model exhibits a competitive prediction accuracy with minimal constraints in a geometric representation.