Inferring Change Points in High-Dimensional Linear Regression via Approximate Message Passing

We consider the problem of localizing change points in high-dimensional linear regression. We propose an Approximate Message Passing (AMP) algorithm for estimating both the signals and the change point locations. Assuming Gaussian covariates, we give an exact asymptotic characterization of its estimation performance in the limit where the number of samples grows proportionally to the signal dimension. Our algorithm can be tailored to exploit any prior information on the signal, noise, and change points. It also enables uncertainty quantification in the form of an efficiently computable approximate posterior distribution, whose asymptotic form we characterize exactly. We validate our theory via numerical experiments, and demonstrate the favorable performance of our estimators on both synthetic data and images.

Coded Many-User Multiple Access via Approximate Message Passing

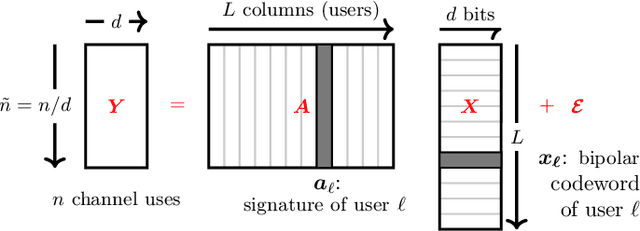
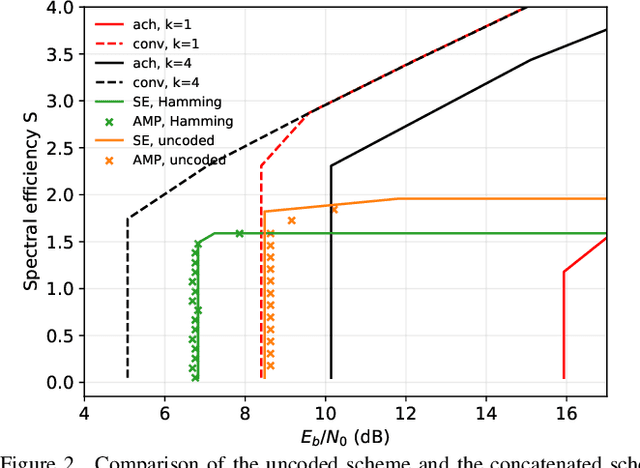
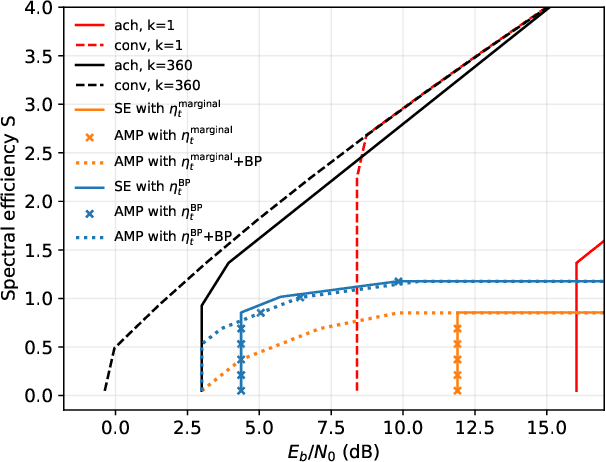
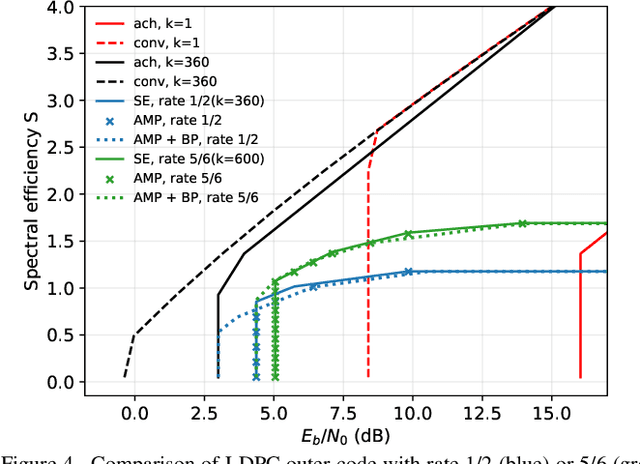
We consider communication over the Gaussian multiple-access channel in the regime where the number of users grows linearly with the codelength. We investigate coded CDMA schemes where each user's information is encoded via a linear code before being modulated with a signature sequence. We propose an efficient approximate message passing (AMP) decoder that can be tailored to the structure of the linear code, and provide an exact asymptotic characterization of its performance. Based on this result, we consider a decoder that integrates AMP and belief propagation and characterize the tradeoff between spectral efficiency and signal-to-noise ratio, for a given target error rate. Simulation results are provided to demonstrate the benefits of the concatenated scheme at finite lengths.

Sketching sparse low-rank matrices with near-optimal sample- and time-complexity

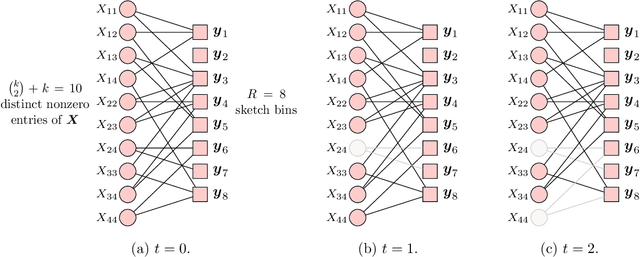
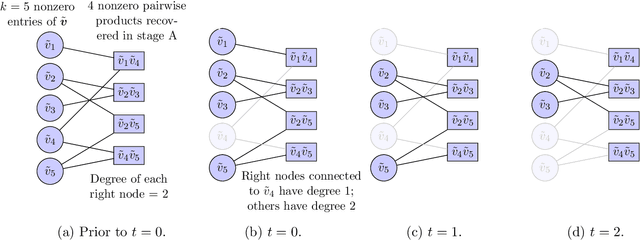
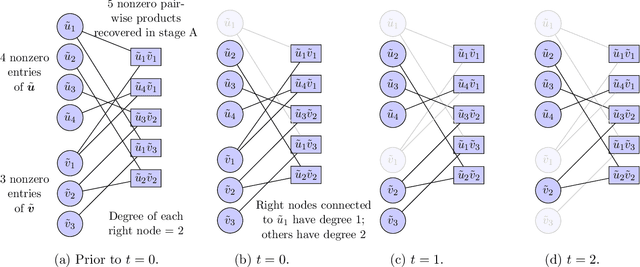
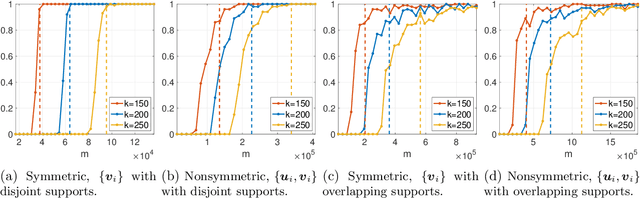
We consider the problem of recovering an $n_1 \times n_2$ low-rank matrix with $k$-sparse singular vectors from a small number of linear measurements (sketch). We propose a sketching scheme and an algorithm that can recover the singular vectors with high probability, with a sample complexity and running time that both depend only on $k$ and not on the ambient dimensions $n_1$ and $n_2$. Our sketching operator, based on a scheme for compressed sensing by Li et al. and Bakshi et al., uses a combination of a sparse parity check matrix and a partial DFT matrix. Our main contribution is the design and analysis of a two-stage iterative algorithm which recovers the singular vectors by exploiting the simultaneously sparse and low-rank structure of the matrix. We derive a nonasymptotic bound on the probability of exact recovery. We also show how the scheme can be adapted to tackle matrices that are approximately sparse and low-rank. The theoretical results are validated by numerical simulations.

Learning Personalized Thermal Preferences via Bayesian Active Learning with Unimodality Constraints

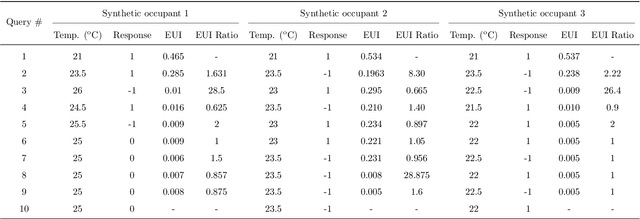
Thermal preferences vary from person to person and may change over time. The main objective of this paper is to sequentially pose intelligent queries to occupants in order to optimally learn the indoor air temperature values which maximize their satisfaction. Our central hypothesis is that an occupant's preference relation over indoor air temperature can be described using a scalar function of these temperatures, which we call the "occupant's thermal utility function". Information about an occupant's preference over these temperatures is available to us through their response to thermal preference queries : "prefer warmer," "prefer cooler" and "satisfied" which we interpret as statements about the derivative of their utility function, i.e. the utility function is "increasing", "decreasing" and "constant" respectively. We model this hidden utility function using a Gaussian process prior with built-in unimodality constraint, i.e., the utility function has a unique maximum, and we train this model using Bayesian inference. This permits an expected improvement based selection of next preference query to pose to the occupant, which takes into account both exploration (sampling from areas of high uncertainty) and exploitation (sampling from areas which are likely to offer an improvement over current best observation). We use this framework to sequentially design experiments and illustrate its benefits by showing that it requires drastically fewer observations to learn the maximally preferred temperature values as compared to other methods. This framework is an important step towards the development of intelligent HVAC systems which would be able to respond to occupants' personalized thermal comfort needs. In order to encourage the use of our PE framework and ensure reproducibility in results, we publish an implementation of our work named GPPrefElicit as an open-source package in Python.