Kuan Hsieh
Coded Many-User Multiple Access via Approximate Message Passing
Feb 08, 2024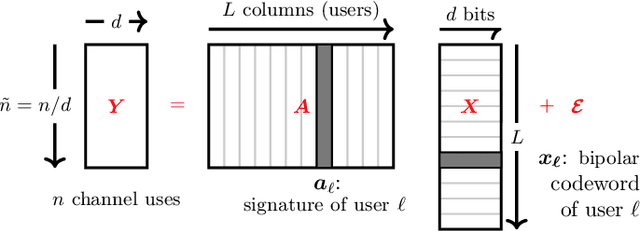
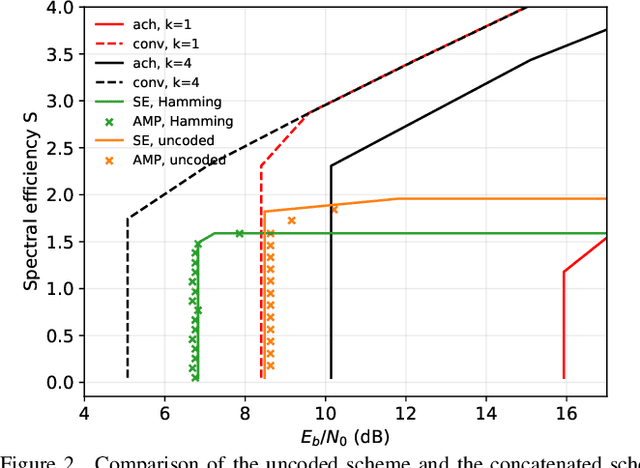
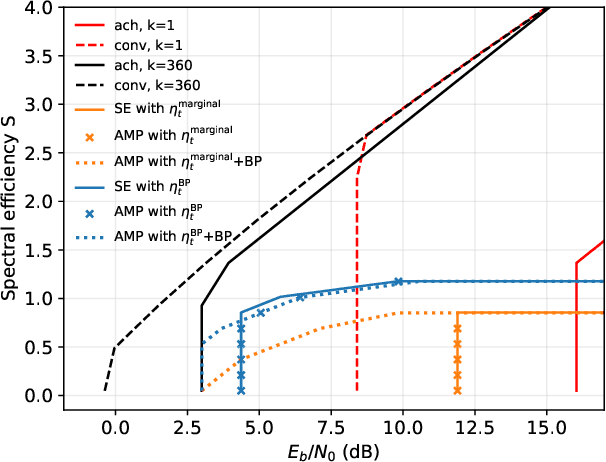
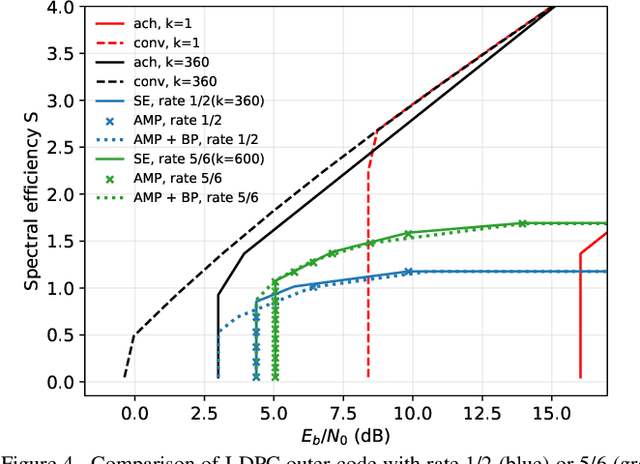
Abstract:We consider communication over the Gaussian multiple-access channel in the regime where the number of users grows linearly with the codelength. We investigate coded CDMA schemes where each user's information is encoded via a linear code before being modulated with a signature sequence. We propose an efficient approximate message passing (AMP) decoder that can be tailored to the structure of the linear code, and provide an exact asymptotic characterization of its performance. Based on this result, we consider a decoder that integrates AMP and belief propagation and characterize the tradeoff between spectral efficiency and signal-to-noise ratio, for a given target error rate. Simulation results are provided to demonstrate the benefits of the concatenated scheme at finite lengths.
Bayes-Optimal Estimation in Generalized Linear Models via Spatial Coupling
Sep 15, 2023Abstract:We consider the problem of signal estimation in a generalized linear model (GLM). GLMs include many canonical problems in statistical estimation, such as linear regression, phase retrieval, and 1-bit compressed sensing. Recent work has precisely characterized the asymptotic minimum mean-squared error (MMSE) for GLMs with i.i.d. Gaussian sensing matrices. However, in many models there is a significant gap between the MMSE and the performance of the best known feasible estimators. In this work, we address this issue by considering GLMs defined via spatially coupled sensing matrices. We propose an efficient approximate message passing (AMP) algorithm for estimation and prove that with a simple choice of spatially coupled design, the MSE of a carefully tuned AMP estimator approaches the asymptotic MMSE in the high-dimensional limit. To prove the result, we first rigorously characterize the asymptotic performance of AMP for a GLM with a generic spatially coupled design. This characterization is in terms of a deterministic recursion (`state evolution') that depends on the parameters defining the spatial coupling. Then, using a simple spatially coupled design and judicious choice of functions defining the AMP, we analyze the fixed points of the resulting state evolution and show that it achieves the asymptotic MMSE. Numerical results for phase retrieval and rectified linear regression show that spatially coupled designs can yield substantially lower MSE than i.i.d. Gaussian designs at finite dimensions when used with AMP algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge