Inferring Change Points in High-Dimensional Linear Regression via Approximate Message Passing

We consider the problem of localizing change points in high-dimensional linear regression. We propose an Approximate Message Passing (AMP) algorithm for estimating both the signals and the change point locations. Assuming Gaussian covariates, we give an exact asymptotic characterization of its estimation performance in the limit where the number of samples grows proportionally to the signal dimension. Our algorithm can be tailored to exploit any prior information on the signal, noise, and change points. It also enables uncertainty quantification in the form of an efficiently computable approximate posterior distribution, whose asymptotic form we characterize exactly. We validate our theory via numerical experiments, and demonstrate the favorable performance of our estimators on both synthetic data and images.

Statistical-Computational Tradeoffs in Mixed Sparse Linear Regression

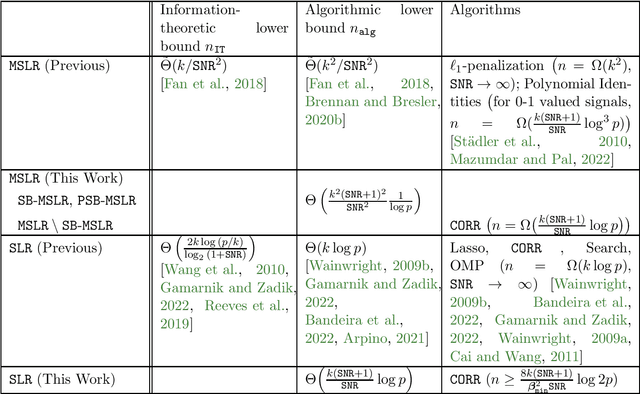
We consider the problem of mixed sparse linear regression with two components, where two real $k$-sparse signals $\beta_1, \beta_2$ are to be recovered from $n$ unlabelled noisy linear measurements. The sparsity is allowed to be sublinear in the dimension, and additive noise is assumed to be independent Gaussian with variance $\sigma^2$. Prior work has shown that the problem suffers from a $\frac{k}{SNR^2}$-to-$\frac{k^2}{SNR^2}$ statistical-to-computational gap, resembling other computationally challenging high-dimensional inference problems such as Sparse PCA and Robust Sparse Mean Estimation; here $SNR$ is the signal-to-noise ratio. We establish the existence of a more extensive computational barrier for this problem through the method of low-degree polynomials, but show that the problem is computationally hard only in a very narrow symmetric parameter regime. We identify a smooth information-computation tradeoff between the sample complexity $n$ and runtime for any randomized algorithm in this hard regime. Via a simple reduction, this provides novel rigorous evidence for the existence of a computational barrier to solving exact support recovery in sparse phase retrieval with sample complexity $n = \tilde{o}(k^2)$. Our second contribution is to analyze a simple thresholding algorithm which, outside of the narrow regime where the problem is hard, solves the associated mixed regression detection problem in $O(np)$ time with square-root the number of samples and matches the sample complexity required for (non-mixed) sparse linear regression; this allows the recovery problem to be subsequently solved by state-of-the-art techniques from the dense case. As a special case of our results, we show that this simple algorithm is order-optimal among a large family of algorithms in solving exact signed support recovery in sparse linear regression.

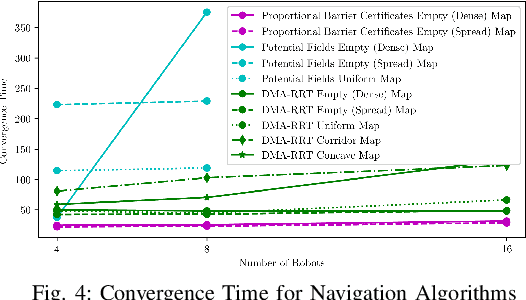
Using Information Invariants to Compare Swarm Algorithms and General Multi-Robot Algorithms: A Technical Report

Robotic swarms are decentralized multi-robot systems whose members use local information from proximal neighbors to execute simple reactive control laws that result in emergent collective behaviors. In contrast, members of a general multi-robot system may have access to global information, all- to-all communication or sophisticated deliberative collabora- tion. Some algorithms in the literature are applicable to robotic swarms. Others require the extra complexity of general multi- robot systems. Given an application domain, a system designer or supervisory operator must choose an appropriate system or algorithm respectively that will enable them to achieve their goals while satisfying mission constraints (e.g. bandwidth, energy, time limits). In this paper, we compare representative swarm and general multi-robot algorithms in two application domains - navigation and dynamic area coverage - with respect to several metrics (e.g. completion time, distance trav- elled). Our objective is to characterize each class of algorithms to inform offline system design decisions by engineers or online algorithm selection decisions by supervisory operators. Our contributions are (a) an empirical performance comparison of representative swarm and general multi-robot algorithms in two application domains, (b) a comparative analysis of the algorithms based on the theory of information invariants, which provides a theoretical characterization supported by our empirical results.