Wrapped Distributions on homogeneous Riemannian manifolds

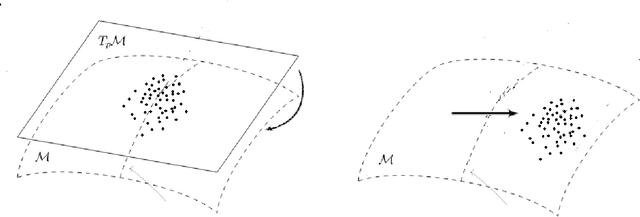
We provide a general framework for constructing probability distributions on Riemannian manifolds, taking advantage of area-preserving maps and isometries. Control over distributions' properties, such as parameters, symmetry and modality yield a family of flexible distributions that are straightforward to sample from, suitable for use within Monte Carlo algorithms and latent variable models, such as autoencoders. As an illustration, we empirically validate our approach by utilizing our proposed distributions within a variational autoencoder and a latent space network model. Finally, we take advantage of the generalized description of this framework to posit questions for future work.

Bayesian Model Averaging for Data Driven Decision Making when Causality is Partially Known

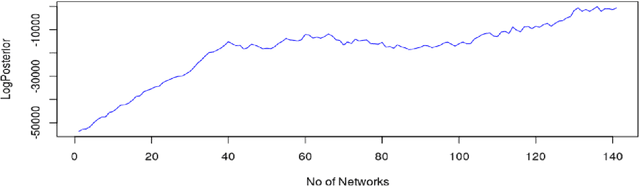
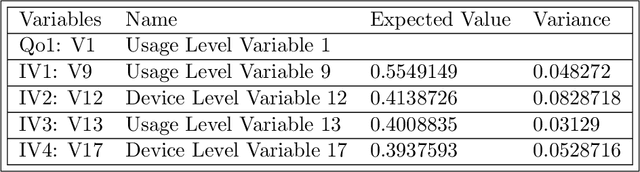
Probabilistic machine learning models are often insufficient to help with decisions on interventions because those models find correlations - not causal relationships. If observational data is only available and experimentation are infeasible, the correct approach to study the impact of an intervention is to invoke Pearl's causality framework. Even that framework assumes that the underlying causal graph is known, which is seldom the case in practice. When the causal structure is not known, one may use out-of-the-box algorithms to find causal dependencies from observational data. However, there exists no method that also accounts for the decision-maker's prior knowledge when developing the causal structure either. The objective of this paper is to develop rational approaches for making decisions from observational data in the presence of causal graph uncertainty and prior knowledge from the decision-maker. We use ensemble methods like Bayesian Model Averaging (BMA) to infer set of causal graphs that can represent the data generation process. We provide decisions by computing the expected value and risk of potential interventions explicitly. We demonstrate our approach by applying them in different example contexts.

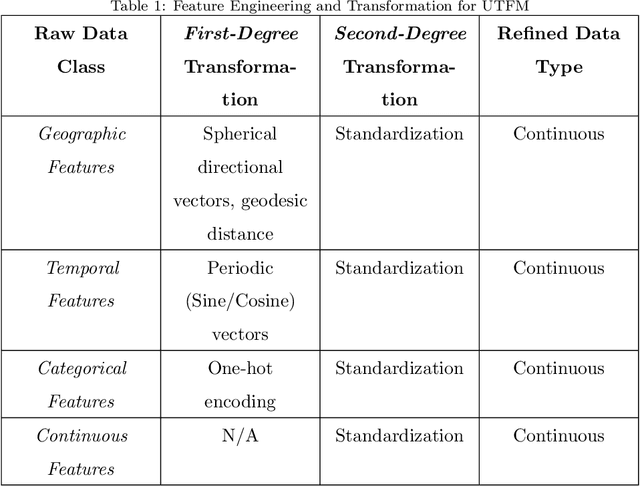
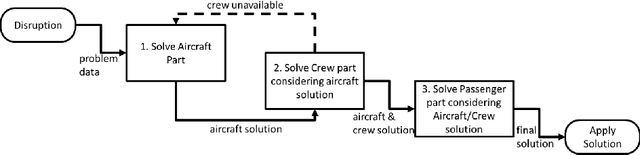
Uncertainty Quantification and Propagation for Airline Disruption Management

Disruption management during the airline scheduling process can be compartmentalized into proactive and reactive processes depending upon the time of schedule execution. The state of the art for decision-making in airline disruption management involves a heuristic human-centric approach that does not categorically study uncertainty in proactive and reactive processes for managing airline schedule disruptions. Hence, this paper introduces an uncertainty transfer function model (UTFM) framework that characterizes uncertainty for proactive airline disruption management before schedule execution, reactive airline disruption management during schedule execution, and proactive airline disruption management after schedule execution to enable the construction of quantitative tools that can allow an intelligent agent to rationalize complex interactions and procedures for robust airline disruption management. Specifically, we use historical scheduling and operations data from a major U.S. airline to facilitate the development and assessment of the UTFM, defined by hidden Markov models (a special class of probabilistic graphical models) that can efficiently perform pattern learning and inference on portions of large data sets.