Wrapped Distributions on homogeneous Riemannian manifolds

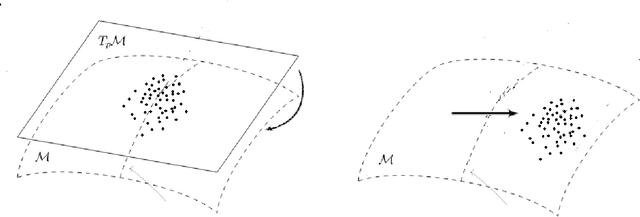
We provide a general framework for constructing probability distributions on Riemannian manifolds, taking advantage of area-preserving maps and isometries. Control over distributions' properties, such as parameters, symmetry and modality yield a family of flexible distributions that are straightforward to sample from, suitable for use within Monte Carlo algorithms and latent variable models, such as autoencoders. As an illustration, we empirically validate our approach by utilizing our proposed distributions within a variational autoencoder and a latent space network model. Finally, we take advantage of the generalized description of this framework to posit questions for future work.

Lasso for hierarchical polynomial models

In a polynomial regression model, the divisibility conditions implicit in polynomial hierarchy give way to a natural construction of constraints for the model parameters. We use this principle to derive versions of strong and weak hierarchy and to extend existing work in the literature, which at the moment is only concerned with models of degree two. We discuss how to estimate parameters in lasso using standard quadratic programming techniques and apply our proposal to both simulated data and examples from the literature. The proposed methodology compares favorably with existing techniques in terms of low validation error and model size.