Wrapped Distributions on homogeneous Riemannian manifolds

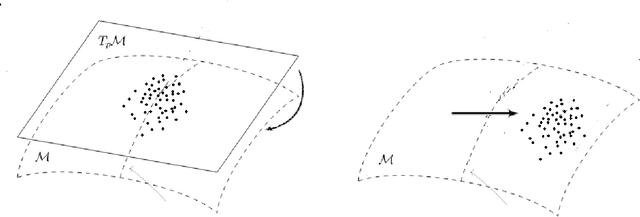
We provide a general framework for constructing probability distributions on Riemannian manifolds, taking advantage of area-preserving maps and isometries. Control over distributions' properties, such as parameters, symmetry and modality yield a family of flexible distributions that are straightforward to sample from, suitable for use within Monte Carlo algorithms and latent variable models, such as autoencoders. As an illustration, we empirically validate our approach by utilizing our proposed distributions within a variational autoencoder and a latent space network model. Finally, we take advantage of the generalized description of this framework to posit questions for future work.

Quantifying homologous proteins and proteoforms

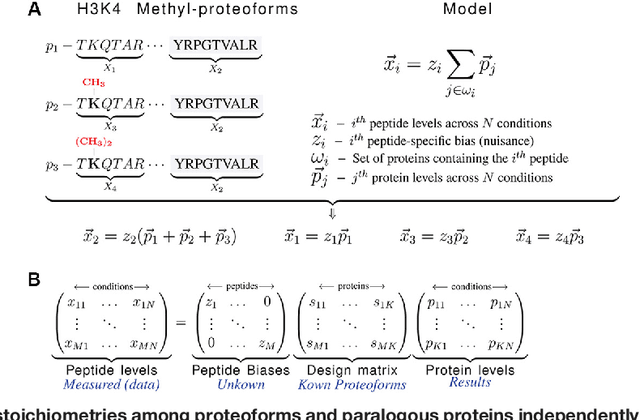
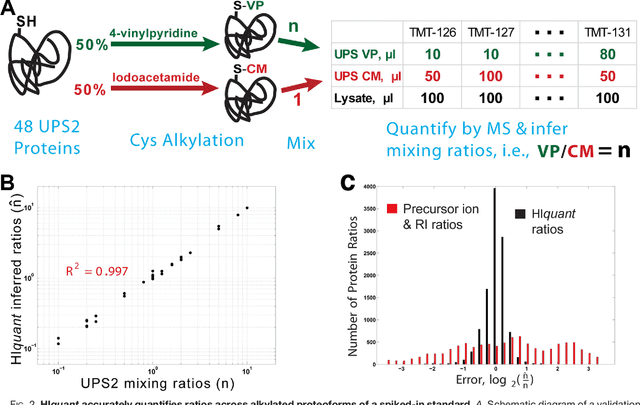
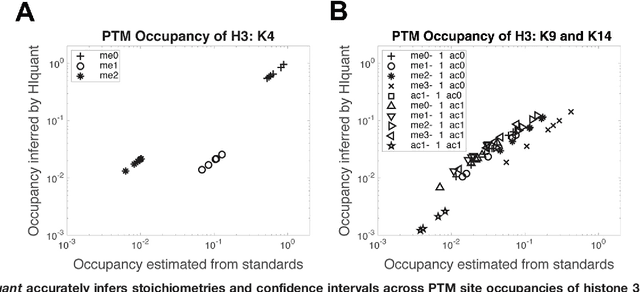
Many proteoforms - arising from alternative splicing, post-translational modifications (PTMs), or paralogous genes - have distinct biological functions, such as histone PTM proteoforms. However, their quantification by existing bottom-up mass-spectrometry (MS) methods is undermined by peptide-specific biases. To avoid these biases, we developed and implemented a first-principles model (HIquant) for quantifying proteoform stoichiometries. We characterized when MS data allow inferring proteoform stoichiometries by HIquant, derived an algorithm for optimal inference, and demonstrated experimentally high accuracy in quantifying fractional PTM occupancy without using external standards, even in the challenging case of the histone modification code. HIquant server is implemented at: https://web.northeastern.edu/slavov/2014_HIquant/

Inference of Network Summary Statistics Through Network Denoising

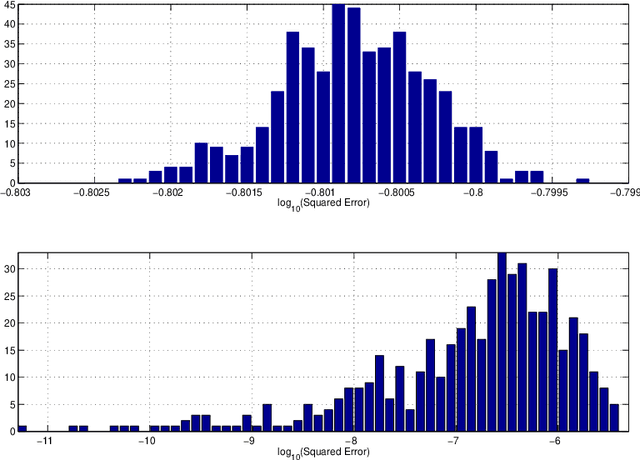
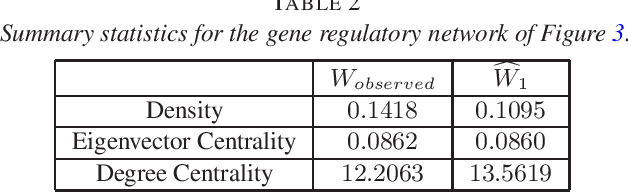
Consider observing an undirected network that is `noisy' in the sense that there are Type I and Type II errors in the observation of edges. Such errors can arise, for example, in the context of inferring gene regulatory networks in genomics or functional connectivity networks in neuroscience. Given a single observed network then, to what extent are summary statistics for that network representative of their analogues for the true underlying network? Can we infer such statistics more accurately by taking into account the noise in the observed network edges? In this paper, we answer both of these questions. In particular, we develop a spectral-based methodology using the adjacency matrix to `denoise' the observed network data and produce more accurate inference of the summary statistics of the true network. We characterize performance of our methodology through bounds on appropriate notions of risk in the $L^2$ sense, and conclude by illustrating the practical impact of this work on synthetic and real-world data.