Quantifying homologous proteins and proteoforms

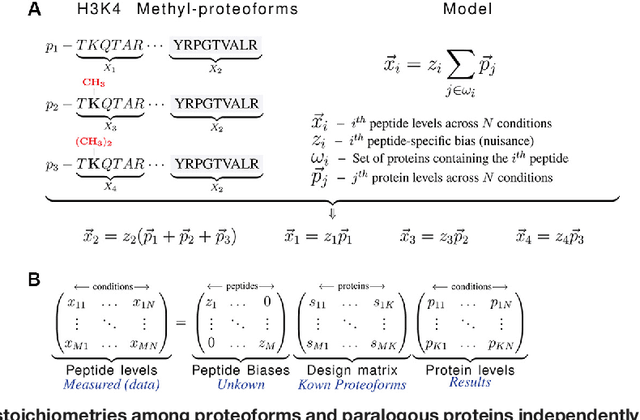
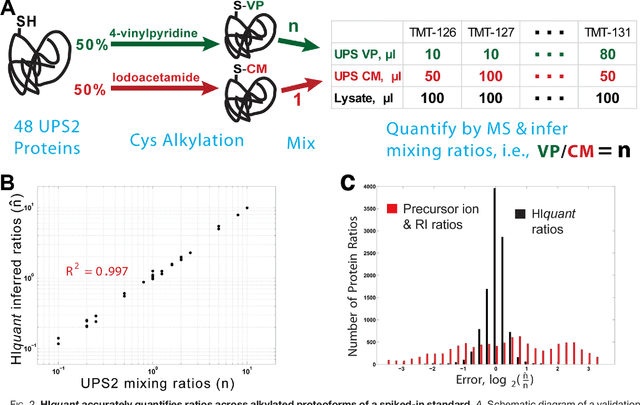
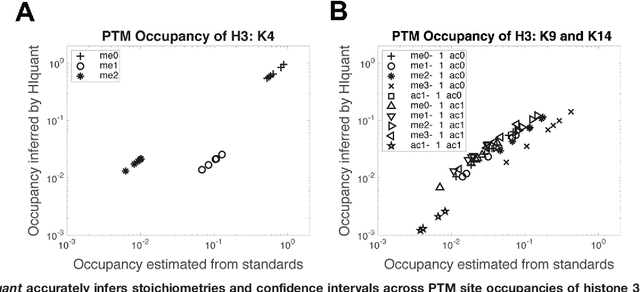
Many proteoforms - arising from alternative splicing, post-translational modifications (PTMs), or paralogous genes - have distinct biological functions, such as histone PTM proteoforms. However, their quantification by existing bottom-up mass-spectrometry (MS) methods is undermined by peptide-specific biases. To avoid these biases, we developed and implemented a first-principles model (HIquant) for quantifying proteoform stoichiometries. We characterized when MS data allow inferring proteoform stoichiometries by HIquant, derived an algorithm for optimal inference, and demonstrated experimentally high accuracy in quantifying fractional PTM occupancy without using external standards, even in the challenging case of the histone modification code. HIquant server is implemented at: https://web.northeastern.edu/slavov/2014_HIquant/

Inference of Sparse Networks with Unobserved Variables. Application to Gene Regulatory Networks

Networks are a unifying framework for modeling complex systems and network inference problems are frequently encountered in many fields. Here, I develop and apply a generative approach to network inference (RCweb) for the case when the network is sparse and the latent (not observed) variables affect the observed ones. From all possible factor analysis (FA) decompositions explaining the variance in the data, RCweb selects the FA decomposition that is consistent with a sparse underlying network. The sparsity constraint is imposed by a novel method that significantly outperforms (in terms of accuracy, robustness to noise, complexity scaling, and computational efficiency) Bayesian methods and MLE methods using l1 norm relaxation such as K-SVD and l1--based sparse principle component analysis (PCA). Results from simulated models demonstrate that RCweb recovers exactly the model structures for sparsity as low (as non-sparse) as 50% and with ratio of unobserved to observed variables as high as 2. RCweb is robust to noise, with gradual decrease in the parameter ranges as the noise level increases.

Convex Total Least Squares

We study the total least squares (TLS) problem that generalizes least squares regression by allowing measurement errors in both dependent and independent variables. TLS is widely used in applied fields including computer vision, system identification and econometrics. The special case when all dependent and independent variables have the same level of uncorrelated Gaussian noise, known as ordinary TLS, can be solved by singular value decomposition (SVD). However, SVD cannot solve many important practical TLS problems with realistic noise structure, such as having varying measurement noise, known structure on the errors, or large outliers requiring robust error-norms. To solve such problems, we develop convex relaxation approaches for a general class of structured TLS (STLS). We show both theoretically and experimentally, that while the plain nuclear norm relaxation incurs large approximation errors for STLS, the re-weighted nuclear norm approach is very effective, and achieves better accuracy on challenging STLS problems than popular non-convex solvers. We describe a fast solution based on augmented Lagrangian formulation, and apply our approach to an important class of biological problems that use population average measurements to infer cell-type and physiological-state specific expression levels that are very hard to measure directly.