Prakash Balachandran
Inference of Network Summary Statistics Through Network Denoising
Dec 31, 2013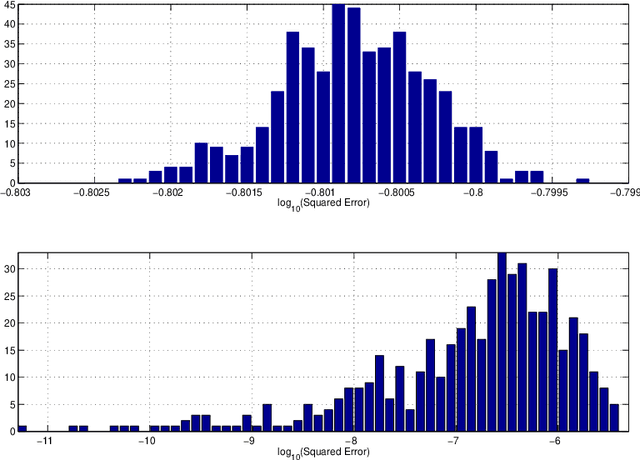


Abstract:Consider observing an undirected network that is `noisy' in the sense that there are Type I and Type II errors in the observation of edges. Such errors can arise, for example, in the context of inferring gene regulatory networks in genomics or functional connectivity networks in neuroscience. Given a single observed network then, to what extent are summary statistics for that network representative of their analogues for the true underlying network? Can we infer such statistics more accurately by taking into account the noise in the observed network edges? In this paper, we answer both of these questions. In particular, we develop a spectral-based methodology using the adjacency matrix to `denoise' the observed network data and produce more accurate inference of the summary statistics of the true network. We characterize performance of our methodology through bounds on appropriate notions of risk in the $L^2$ sense, and conclude by illustrating the practical impact of this work on synthetic and real-world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge