Wrapped Distributions on homogeneous Riemannian manifolds

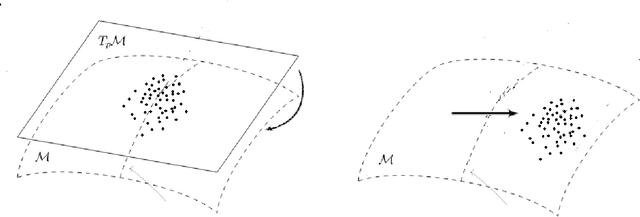
We provide a general framework for constructing probability distributions on Riemannian manifolds, taking advantage of area-preserving maps and isometries. Control over distributions' properties, such as parameters, symmetry and modality yield a family of flexible distributions that are straightforward to sample from, suitable for use within Monte Carlo algorithms and latent variable models, such as autoencoders. As an illustration, we empirically validate our approach by utilizing our proposed distributions within a variational autoencoder and a latent space network model. Finally, we take advantage of the generalized description of this framework to posit questions for future work.

Gaussian Processes on Hypergraphs

We derive a Matern Gaussian process (GP) on the vertices of a hypergraph. This enables estimation of regression models of observed or latent values associated with the vertices, in which the correlation and uncertainty estimates are informed by the hypergraph structure. We further present a framework for embedding the vertices of a hypergraph into a latent space using the hypergraph GP. Finally, we provide a scheme for identifying a small number of representative inducing vertices that enables scalable inference through sparse GPs. We demonstrate the utility of our framework on three challenging real-world problems that concern multi-class classification for the political party affiliation of legislators on the basis of voting behaviour, probabilistic matrix factorisation of movie reviews, and embedding a hypergraph of animals into a low-dimensional latent space.