Ensemble learning of the atrial fiber orientation with physics-informed neural networks

The anisotropic structure of the myocardium is a key determinant of the cardiac function. To date, there is no imaging modality to assess in-vivo the cardiac fiber structure. We recently proposed Fibernet, a method for the automatic identification of the anisotropic conduction -- and thus fibers -- in the atria from local electrical recordings. Fibernet uses cardiac activation as recorded during electroanatomical mappings to infer local conduction properties using physics-informed neural networks. In this work, we extend Fibernet to cope with the uncertainty in the estimated fiber field. Specifically, we use an ensemble of neural networks to produce multiple samples, all fitting the observed data, and compute posterior statistics. We also introduce a methodology to select the best fiber orientation members and define the input of the neural networks directly on the atrial surface. With these improvements, we outperform the previous methodology in terms of fiber orientation error in 8 different atrial anatomies. Currently, our approach can estimate the fiber orientation and conduction velocities in under 7 minutes with quantified uncertainty, which opens the door to its application in clinical practice. We hope the proposed methodology will enable further personalization of cardiac digital twins for precision medicine.

Finite element-based space-time total variation-type regularization of the inverse problem in electrocardiographic imaging

Reconstructing cardiac electrical activity from body surface electric potential measurements results in the severely ill-posed inverse problem in electrocardiography. Many different regularization approaches have been proposed to improve numerical results and provide unique results. This work presents a novel approach for reconstructing the epicardial potential from body surface potential maps based on a space-time total variation-type regularization using finite elements, where a first-order primal-dual algorithm solves the underlying convex optimization problem. In several numerical experiments, the superior performance of this method and the benefit of space-time regularization for the reconstruction of epicardial potential on two-dimensional torso data and a three-dimensional rabbit heart compared to state-of-the-art methods are demonstrated.

Probabilistic learning of the Purkinje network from the electrocardiogram

The identification of the Purkinje conduction system in the heart is a challenging task, yet essential for a correct definition of cardiac digital twins for precision cardiology. Here, we propose a probabilistic approach for identifying the Purkinje network from non-invasive clinical data such as the standard electrocardiogram (ECG). We use cardiac imaging to build an anatomically accurate model of the ventricles; we algorithmically generate a rule-based Purkinje network tailored to the anatomy; we simulate physiological electrocardiograms with a fast model; we identify the geometrical and electrical parameters of the Purkinje-ECG model with Bayesian optimization and approximate Bayesian computation. The proposed approach is inherently probabilistic and generates a population of plausible Purkinje networks, all fitting the ECG within a given tolerance. In this way, we can estimate the uncertainty of the parameters, thus providing reliable predictions. We test our methodology in physiological and pathological scenarios, showing that we are able to accurately recover the ECG with our model. We propagate the uncertainty in the Purkinje network parameters in a simulation of conduction system pacing therapy. Our methodology is a step forward in creation of digital twins from non-invasive data in precision medicine. An open source implementation can be found at http://github.com/fsahli/purkinje-learning

Shape of my heart: Cardiac models through learned signed distance functions

The efficient construction of an anatomical model is one of the major challenges of patient-specific in-silico models of the human heart. Current methods frequently rely on linear statistical models, allowing no advanced topological changes, or requiring medical image segmentation followed by a meshing pipeline, which strongly depends on image resolution, quality, and modality. These approaches are therefore limited in their transferability to other imaging domains. In this work, the cardiac shape is reconstructed by means of three-dimensional deep signed distance functions with Lipschitz regularity. For this purpose, the shapes of cardiac MRI reconstructions are learned from public databases to model the spatial relation of multiple chambers in Cartesian space. We demonstrate that this approach is also capable of reconstructing anatomical models from partial data, such as point clouds from a single ventricle, or modalities different from the trained MRI, such as electroanatomical mapping, and in addition, allows us to generate new anatomical shapes by randomly sampling latent vectors.

Digital twinning of cardiac electrophysiology models from the surface ECG: a geodesic backpropagation approach

The eikonal equation has become an indispensable tool for modeling cardiac electrical activation accurately and efficiently. In principle, by matching clinically recorded and eikonal-based electrocardiograms (ECGs), it is possible to build patient-specific models of cardiac electrophysiology in a purely non-invasive manner. Nonetheless, the fitting procedure remains a challenging task. The present study introduces a novel method, Geodesic-BP, to solve the inverse eikonal problem. Geodesic-BP is well-suited for GPU-accelerated machine learning frameworks, allowing us to optimize the parameters of the eikonal equation to reproduce a given ECG. We show that Geodesic-BP can reconstruct a simulated cardiac activation with high accuracy in a synthetic test case, even in the presence of modeling inaccuracies. Furthermore, we apply our algorithm to a publicly available dataset of a rabbit model, with very positive results. Given the future shift towards personalized medicine, Geodesic-BP has the potential to help in future functionalizations of cardiac models meeting clinical time constraints while maintaining the physiological accuracy of state-of-the-art cardiac models.

$Δ$-PINNs: physics-informed neural networks on complex geometries

Physics-informed neural networks (PINNs) have demonstrated promise in solving forward and inverse problems involving partial differential equations. Despite recent progress on expanding the class of problems that can be tackled by PINNs, most of existing use-cases involve simple geometric domains. To date, there is no clear way to inform PINNs about the topology of the domain where the problem is being solved. In this work, we propose a novel positional encoding mechanism for PINNs based on the eigenfunctions of the Laplace-Beltrami operator. This technique allows to create an input space for the neural network that represents the geometry of a given object. We approximate the eigenfunctions as well as the operators involved in the partial differential equations with finite elements. We extensively test and compare the proposed methodology against traditional PINNs in complex shapes, such as a coil, a heat sink and a bunny, with different physics, such as the Eikonal equation and heat transfer. We also study the sensitivity of our method to the number of eigenfunctions used, as well as the discretization used for the eigenfunctions and the underlying operators. Our results show excellent agreement with the ground truth data in cases where traditional PINNs fail to produce a meaningful solution. We envision this new technique will expand the effectiveness of PINNs to more realistic applications.

Learning cardiac activation maps from 12-lead ECG with multi-fidelity Bayesian optimization on manifolds

We propose a method for identifying an ectopic activation in the heart non-invasively. Ectopic activity in the heart can trigger deadly arrhythmias. The localization of the ectopic foci or earliest activation sites (EASs) is therefore a critical information for cardiologists in deciding the optimal treatment. In this work, we formulate the identification problem as a global optimization problem, by minimizing the mismatch between the ECG predicted by a cardiac model, when paced at a given EAS, and the observed ECG during the ectopic activity. Our cardiac model amounts at solving an anisotropic eikonal equation for cardiac activation and the forward bidomain model in the torso with the lead field approach for computing the ECG. We build a Gaussian process surrogate model of the loss function on the heart surface to perform Bayesian optimization. In this procedure, we iteratively evaluate the loss function following the lower confidence bound criterion, which combines exploring the surface with exploitation of the minimum region. We also extend this framework to incorporate multiple levels of fidelity of the model. We show that our procedure converges to the minimum only after $11.7\pm10.4$ iterations (20 independent runs) for the single-fidelity case and $3.5\pm1.7$ iterations for the multi-fidelity case. We envision that this tool could be applied in real time in a clinical setting to identify potentially dangerous EASs.

Physics-informed neural networks to learn cardiac fiber orientation from multiple electroanatomical maps

We propose FiberNet, a method to estimate in-vivo the cardiac fiber architecture of the human atria from multiple catheter recordings of the electrical activation. Cardiac fibers play a central rolein the electro-mechanical function of the heart, yet they aredifficult to determine in-vivo, and hence rarely truly patient-specificin existing cardiac models.FiberNet learns the fibers arrangement by solvingan inverse problem with physics-informed neural networks. The inverse problem amounts to identifyingthe conduction velocity tensor of a cardiac propagation modelfrom a set of sparse activation maps. The use of multiple mapsenables the simultaneous identification of all the componentsof the conduction velocity tensor, including the local fiber angle.We extensively test FiberNet on synthetic 2-D and 3-D examples, diffusion tensor fibers, and a patient-specific case. We show that 3 maps are sufficient to accurately capture the fibers, also in thepresence of noise. With fewer maps, the role of regularization becomesprominent. Moreover, we show that the fitted model can robustlyreproduce unseen activation maps. We envision that FiberNet will help the creation of patient-specific models for personalized medicine.The full code is available at http://github.com/fsahli/FiberNet.

Smoothness and continuity of cost functionals for ECG mismatch computation

The field of cardiac electrophysiology tries to abstract, describe and finally model the electrical characteristics of a heartbeat. With recent advances in cardiac electrophysiology, models have become more powerful and descriptive as ever. However, to advance to the field of inverse electrophysiological modeling, i.e. creating models from electrical measurements such as the ECG, the less investigated field of smoothness of the simulated ECGs w.r.t. model parameters need to be further explored. The present paper discusses smoothness in terms of the whole pipeline which describes how from physiological parameters, we arrive at the simulated ECG. Employing such a pipeline, we create a test-bench of a simplified idealized left ventricle model and demonstrate the most important factors for efficient inverse modeling through smooth cost functionals. Such knowledge will be important for designing and creating inverse models in future optimization and machine learning methods.

Fast characterization of inducible regions of atrial fibrillation models with multi-fidelity Gaussian process classification

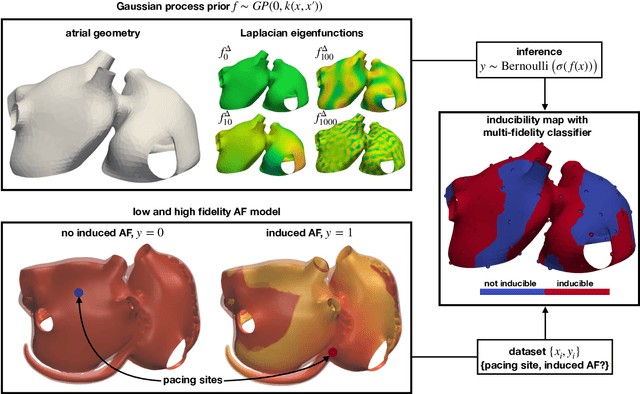
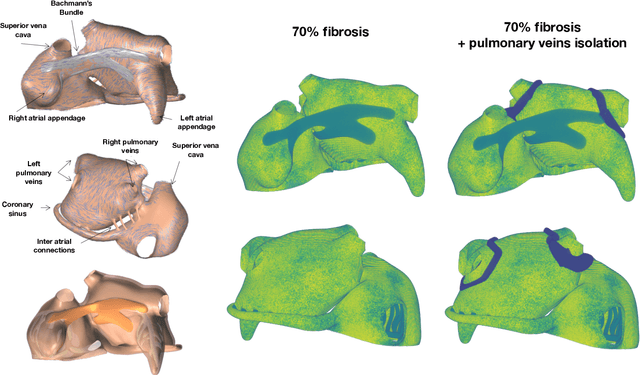
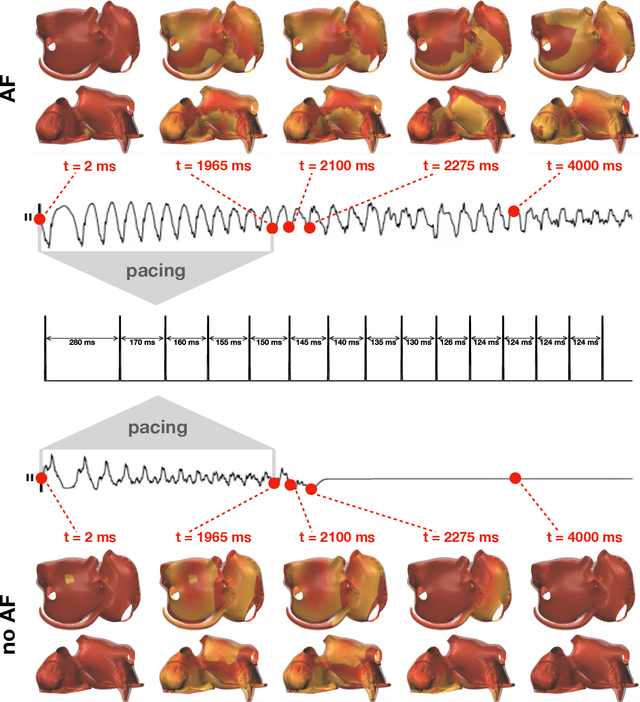
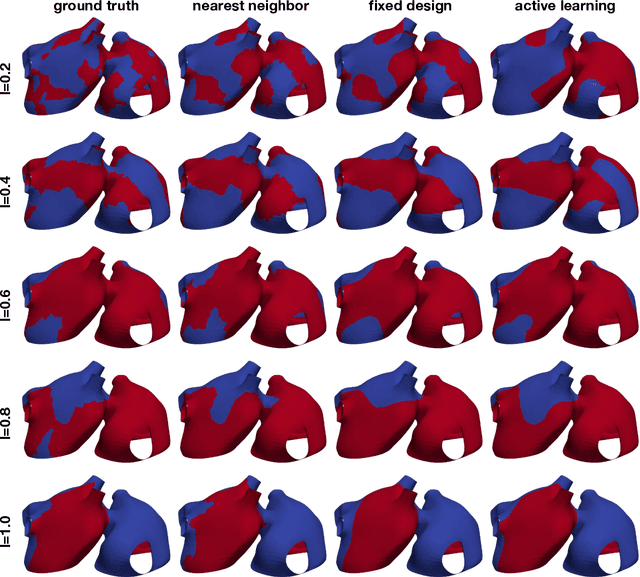
Computational models of atrial fibrillation have successfully been used to predict optimal ablation sites. A critical step to assess the effect of an ablation pattern is to pace the model from different, potentially random, locations to determine whether arrhythmias can be induced in the atria. In this work, we propose to use multi-fidelity Gaussian process classification on Riemannian manifolds to efficiently determine the regions in the atria where arrhythmias are inducible. We build a probabilistic classifier that operates directly on the atrial surface. We take advantage of lower resolution models to explore the atrial surface and combine seamlessly with high-resolution models to identify regions of inducibility. When trained with 40 samples, our multi-fidelity classifier shows a balanced accuracy that is 10% higher than a nearest neighbor classifier used as a baseline atrial fibrillation model, and 9% higher in presence of atrial fibrillation with ablations. We hope that this new technique will allow faster and more precise clinical applications of computational models for atrial fibrillation.